定义

一般情况下，若“傅里叶变换”一词不加任何限定语，则指的是“连续傅里叶变换”（连续函数的傅里叶变换）。定义傅里叶变换有许多不同的方式。本文中采用如下的定义：(连续)傅里叶变换将可积函数 f : R → → --> C {\displaystyle f:\mathbb {R} \rightarrow \mathbb {C} } 表示成复指数函数的积分或级数形式。

当自变量x表示时间（以秒为单位），变换变量ξ表示频率（以赫兹为单位）。在适当条件下， f ^ ^ --> {\displaystyle {\hat {f}}} 可由逆变换（inverse Fourier transform）由下式确定 f {\displaystyle f} ：

傅里叶逆定理提出 f {\displaystyle f} 可由 f ^ ^ --> {\displaystyle {\hat {f}}} 傅立叶傅立叶在其1822年出版的著作《热分析理论》（法语：Théorie analytique de la chaleur）中首次引入这个定理。虽然现在标准下的证明直到很久以后才出现。 f {\displaystyle f} 和 f ^ ^ --> {\displaystyle {\hat {f}}} 常常被称为傅立叶积分对 或傅立叶变换对。

简介

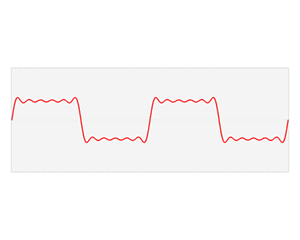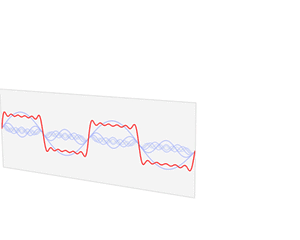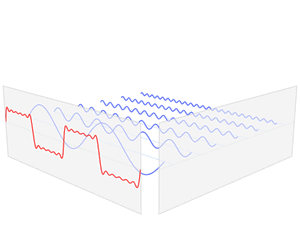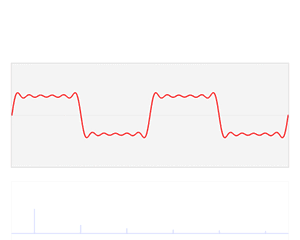
傅里叶变换将函数的时域（红色）与频域（蓝色）相关联。频谱中的不同成分频率在频域中以峰值形式表示。

傅里叶变换源自对傅里叶级数的研究。在对傅里叶级数的研究中，复杂的周期函数可以用一系列简单的正弦、余弦波之和表示。傅里叶变换是对傅里叶级数的扩展，由它表示的函数的周期趋近于无穷。

中文译名

英语：Fourier transform 或 法语：Transformée de Fourier 中文较常用的翻译名称有“傅立叶变换”、“付立叶变换”等等。为方便起见，本文统一写作“傅里叶变换”。

应用

傅里叶变换在数据科学、物理学、声学、光学、结构动力学、量子力学、数论、组合数学、概率论、统计学、信号处理、密码学、海洋学、通讯、金融等领域都有着广泛的应用。例如在信号处理中，傅里叶变换的典型用途是将信号分解成振幅分量和频率分量。

基本性质

线性性质

两函数之和的傅里叶变换等于各自变换之和。数学描述是：若函数 f ( x ) {\displaystyle f\left(x\right)} 和 g ( x ) {\displaystyle g\left(x\right)} 的傅里叶变换 F [ f ] {\displaystyle {\mathcal {F}}[f]} 和 F [ g ] {\displaystyle {\mathcal {F}}[g]} 都存在， α α --> {\displaystyle \alpha } 和 β β --> {\displaystyle \beta } 为任意常系数，则 F [ α α --> f + β β --> g ] = α α --> F [ f ] + β β --> F [ g ] {\displaystyle {\mathcal {F}}[\alpha f+\beta g]=\alpha {\mathcal {F}}[f]+\beta {\mathcal {F}}[g]} ；傅里叶变换算符 F {\displaystyle {\mat幺正算符 {F}}} 可经归一化成为幺正算符。

平移性质

若函数 f ( x ) {\displaystyle f\left(x\right)} 存在傅里叶变换，则对任意实数 ω ω --> 0 {\displaystyle \omega _{0}} ，函数 f ( x ) e i ω ω --> 0 x {\displaystyle f(x)e^{i\omega _{0}x}} 也存在傅里叶变换，且有 F [ f ( x ) e i ω ω --> 0 x ] = F ( ω ω --> − − --> ω ω --> 0 ) {\displaystyle {\mathcal {F}}[f(x)e^{i\omega _{0}x}]=F(\omega -\omega _{0})} 。式中花体 F {\displaystyle {\mathcal {F}}} 是傅里叶变换的作用算子，平体 F {\displaystyle F} 表示变换的结果（复函数）， e {自然对数playstyle e} 为自然对数的底， i {虚数isplaystyle i} 为虚数单位 − − --> 1 {\displaystyle {\sqrt {-1}}} 。

微分关系

若函数 f ( x ) {\displaystyle f\left(x\right)} 当 | x | → → --> ∞ ∞ --> {\displaystyle |x|\rightarrow \inft极限} 时的极限为0，而其导函数 f ′ ( x ) {\displaystyle f"(x)} 的傅里叶变换存在，则有 F [ f ′ ( x ) ] = i ω ω --> F [ f ( x ) ] {\displaystyle {\mathcal {F}}[f"(x)]=i\omega {\mathcal {F}}[f(x)]} ，即导函数的傅里叶变换等于原函数的傅里叶变换乘以因子 i ω ω --> {\displaystyle i\omega } 。更一般地，若 f ( ± ± --> ∞ ∞ --> ) = f ′ ( ± ± --> ∞ ∞ --> ) = … … --> = f ( k − − --> 1 ) ( ± ± --> ∞ ∞ --> ) = 0 {\displaystyle f(\pm \infty )=f"(\pm \infty )=\ldots =f^{(k-1)}(\pm \infty )=0} ，且 F [ f ( k ) ( x ) ] {\displaystyle {\mathcal {F}}[f^{(k)}(x)]} 存在，则 F [ f ( k ) ( x ) ] = ( i ω ω --> ) k F [ f ] {\displaystyle {\mathcal {F}}[f^{(k)}(x)]=(i\omega )^{k}{\mathcal {F}}[f]} ，即k阶导数的傅里叶变换等于原函数的傅里叶变换乘以因子 ( i ω ω --> ) k {\displaystyle (i\omega )^{k}} 。

卷积特性

若函数 f ( x ) {\displaystyle f\left(x\right)} 及 g ( x ) {\displaystyle g\left(x\right)} 都在 ( − − --> ∞ ∞ --> , + ∞ ∞ --> ) {\displaystyle (-\infty ,+\infty )} 上绝对可积，则卷积函数 f ∗ ∗ --> g = ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> f ( x − − --> ξ ξ --> ) g ( ξ ξ --> ) d ξ ξ --> {\displaystyle f*g=\int _{-\infty }^{+\infty }f(x-\xi )g(\xi )d\xi } （或者 f ∗ ∗ --> g = ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> f ( ξ ξ --> ) g ( x − − --> ξ ξ --> ) d ξ ξ --> {\displaystyle f*g=\int _{-\infty }^{+\infty }f(\xi )g(x-\xi )d\xi } ）的傅里叶变换存在，且 F [ f ∗ ∗ --> g ] = F [ f ] ⋅ ⋅ --> F [ g ] {\displaystyle {\mathcal {F}}[f*g]={\mathcal {F}}[f]\cdot {\mathcal {F}}[g]} 。卷积性质的逆形式为 F − − --> 1 [ F ( ω ω --> ) ∗ ∗ --> G ( ω ω --> ) ] = 2 π π --> F − − --> 1 [ F ( ω ω --> ) ] ⋅ ⋅ --> F − − --> 1 [ G ( ω ω --> ) ] {\displaystyle {\mathcal {F}}^{-1}[F(\omega )*G(\omega )]=2\pi {\mathcal {F}}^{-1}[F(\omega )]\cdot {\mathcal {F}}^{-1}[G(\omega )]} ，即两个函数卷积的傅里叶逆变换等于它们各自的傅里叶逆变换的乘积乘以 2 π π --> {\displaystyle 2\pi } 。

帕塞瓦尔定理

若函数 f ( x ) {\displaystyle f\left(x\right)} 可积且平方可积，则 ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> f 2 ( x ) d x = 1 2 π π --> ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> | F ( ω ω --> ) | 2 d ω ω --> {\displaystyle \int _{-\infty }^{+\infty }f^{2}(x)dx={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }|F(\omega )|^{2}d\omega } 。其中 F ( ω ω --> ) {\displaystyle F\left(\omega \right)} 是 f ( x ) {\displaystyle f\left(x\right)} 的傅里叶变换。

更一般化而言，若函数 f ( x ) {\displaystyle f\left(x\right)} 和 g ( x ) {\displaystyle g\left(x\right)} 皆为平方可积函数，则 ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> f ( x ) g ∗ ∗ --> ( x ) d x = 1 2 π π --> ∫ ∫ --> − − --> ∞ ∞ --> + ∞ ∞ --> F ( ω ω --> ) G ∗ ∗ --> ( ω ω --> ) d ω ω --> {\displaystyle \int _{-\infty }^{+\infty }f(x)g^{*}(x)dx={\frac {1}{2\pi }}\int _{-\infty }^{+\infty }F(\omega )G^{*}(\omega )d\omega } 。其中 F ( ω ω --> ) {\displaystyle F\left(\omega \right)} 和 G ( ω ω --> ) {\displaystyle G\left(\omega \right)} 分别是 f ( x ) {\displaystyle f\left(x\right)} 和 g ( x ) {\displaystyle g\left(x\right)} 的傅里叶变换, ∗ ∗ --> {\displaystyle *} 代表复共轭。

傅里叶变换的不同变种

傅立叶变换也可以写成在角频率形式： ω = 2πξ其单位是弧度每秒。

应用ξ=ω/（2π）到上述公式会成为下面的形式：

根据这一形式，（傅里叶）逆变换变为：

若不按照本文中使用的，而像这样定义傅里叶变换，那它将不再是L(R)上的一个酉变换 。另外这样的定义也使傅里叶变换与其逆变换显得不太对称。

另一个形式是把(2π)均匀地分开给傅里叶变换和逆变换，即定义为：

根据这一形式，傅立叶变换是再次成为L(R)上的一个幺正变换。它也恢复了傅立叶变换和逆变换之间的对称。

所有三种形式的变化可以通过对正向和反向变换的复指数核取共轭来实现。核函数的符号必须是相反的。除此之外，选择是习惯问题。

如上所讨论的，一个随机变量的特征函数是相同的傅里叶变换斯蒂尔切斯其分布的测量，但在这种情况下它是典型采取不同的惯例为常数。通常情况下特征函数的定义 E ( e i t ⋅ ⋅ --> X ) = ∫ ∫ --> e i t ⋅ ⋅ --> x d μ μ --> X ( x ) {\displaystyle E(e^{it\cdot X})=\int e^{it\cdot x}d\mu _{X}(x)}

在上面“非统一角频率”形式的情况下，存在的2π无因子出现在任一积分的，或在指数。不同于任何约定的上面出现的，本公约采取的指数符号相反。

傅里叶级数

连续形式的傅里叶变换其实是傅里叶级数（Fourier series）的推广，因为积分其实是一种极限形式的求和算子而已。对于周期函数，其傅里叶级数是存在的：

其中 F n {\displaystyle F_{n}} 为复振幅。对于实值函数，函数的傅里叶级数可以写成：

其中an和bn是实频率分量的振幅。

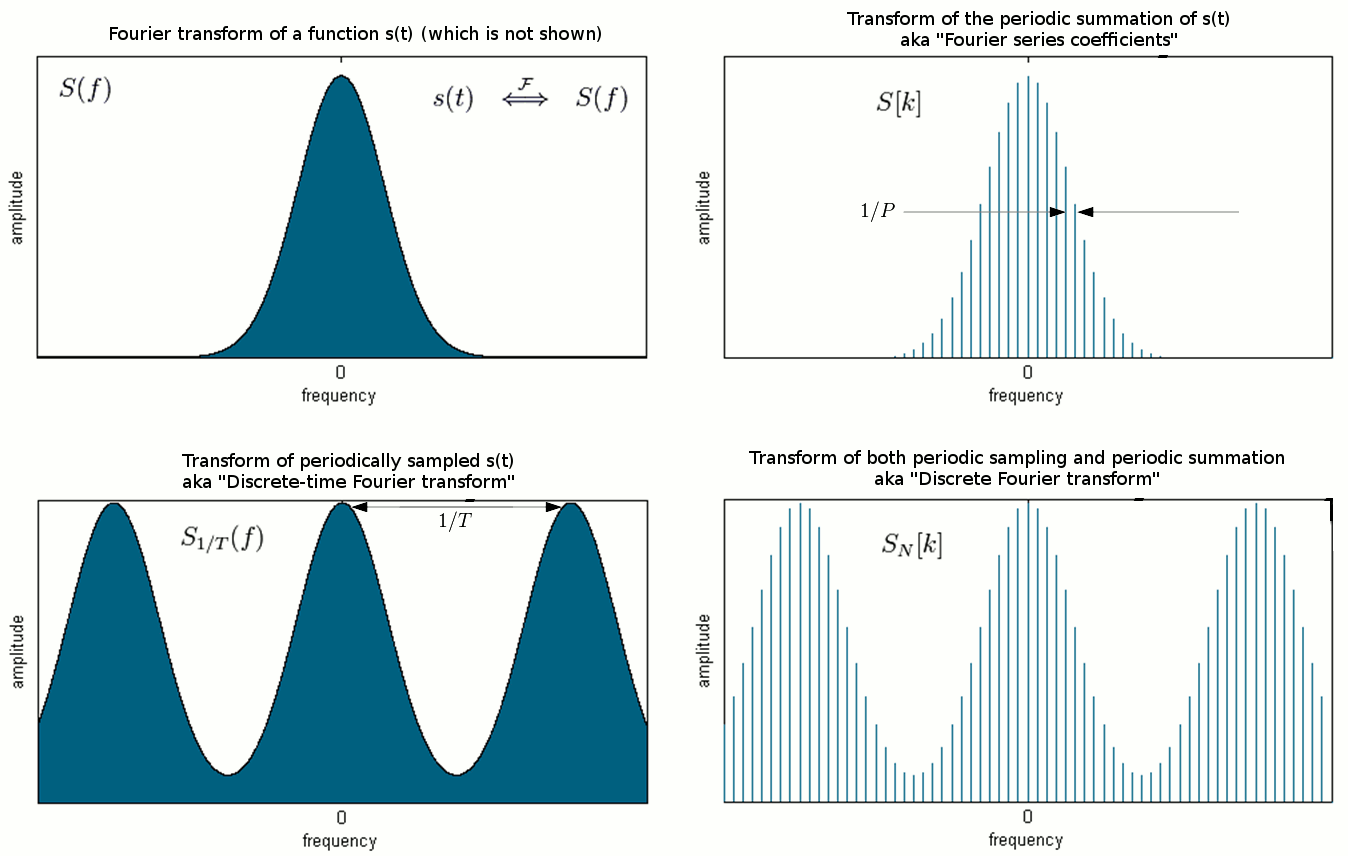
傅里叶分析最初是研究周期性现象，即傅里叶级数的，后来通过傅里叶变换将其推广到了非周期性现象。理解这种推广过程的一种方式是将非周期性现象视为周期性现象的一个特例，即其周期为无限长。

离散时间傅里叶变换

离散傅里叶变换是离散时间傅里叶变换（DTFT）的特例（有时作为后者的近似）。DTFT在时域上离散，在频域上则是周期的。DTFT可以被看作是傅里叶级数的逆转换。

离散傅里叶变换

为了在科学计算和数字信号处理等领域使用计算机进行傅里叶变换，必须将函数xn定义在离散点而非连续域内，且须满足有限性或周期性条件。这种情况下，使用离散傅里叶变换，将函数xn表示为下面的求和形式：

其中 X k {\displaystyle X_{k}} 是傅里叶振幅。直接使用这个公式计算的计算复杂度为 O ( n 2 ) {\displaystyle {\mathcal {O}}(n^{2})} ，而快速傅里叶变换（FFT）可以将复杂度改进为 O ( n log ⁡ ⁡ --> n ) {\displaystyle {\mathcal {O}}(n\log n)} 。计算复杂度的降低以及数字电路计算能力的发展使得DFT成为在信号处理领域十分实用且重要的方法。

在阿贝尔群上的统一描述

以上各种傅里叶变换可以被更统一的表述成任意局部紧致的阿贝尔群上的傅里叶变换。这一问题属于调和分析的范畴。在调和分析中，一个变换从一个群变换到它的对偶群（dual group）。此外，将傅里叶变换与卷积相联系的卷积定理在调和分析中也有类似的结论。傅里叶变换的广义理论基础参见庞特里亚金对偶性（Pontryagin duality）中的介绍。

时频分析变换

小波变换，chirplet转换和分数傅里叶变换试图得到时间信号的频率信息。同时解析频率和时间的能力在数学上受不确定性原理的限制。

傅里叶变换家族

主条目：傅立叶变换家族中的关系

下表列出了傅里叶变换家族的成员。容易发现，函数在时（频）域的离散对应于其像函数在频（时）域的周期性.反之连续则意味着在对应域的信号的非周期性.

常用傅里叶变换表

下面的表记录了一些封闭形式的傅立叶变换。对于函数f(x), g(x)和h(x)，它们的傅立叶变换分别表示为 f ^ ^ --> {\displaystyle {\hat {f}}} , g ^ ^ --> {\displaystyle {\hat {g}}} 和 h ^ ^ --> {\displaystyle {\hat {h}}} 。只包含了三种最常见的形式。注意条目105给出了一个函数的傅里叶变换与其原函数，这可以看作是傅里叶变换及其逆变换的关系。

函数关系

下表列出的常用的傅里叶变换对可以在Erdélyi (1954)或Kammler (2000， appendix)中找到。

平方可积函数

分布

二元函数

400： 变量ξx、ξy、ωx、ωy、νx和νy为实数。 对整个平面积分。

401： 这两个函数都是高斯分布，而且可能不具有单位体积。

402： 此圆有单位半径，如果把circ（t）认作阶梯函数u(1-t); Airy分布用J1（1阶第一类贝塞尔函数）表达。（Stein & Weiss 1971，Thm. IV.3.3）

三元函数

参见

正交变换

傅里叶级数

连续傅里叶变换

离散时间傅里叶变换

离散傅里叶变换

傅里叶分析

拉普拉斯变换

小波变换

参考资料

R. N. Bracewell, The Fourier Transform and Its Applications, 3rd ed., Boston, McGraw Hill, 2000.

电机电子类科《工程数学》，ISBN 957-584-377-0，作者陈锡冠、曾致煌，高立出版社。

Erdélyi, Arthur (编), Tables of Integral Transforms 1, New Your: McGraw-Hill, 1954 

Kammler, David, A First Course in Fourier Analysis, Prentice Hall, 2000, ISBN 0-13-578782-3 

Stein, Elias; Weiss, Guido,Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, 1971, ISBN 978-0-691-08078-9 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。