生平简介

幼年及受教育经历

玻尔兹曼生于奥地利首都维也纳。其父，维希·格奥尔格·玻尔兹曼是一名税吏。他的祖父是一个自柏林移居至维也纳的钟表制造商。而他的母亲卡特琳那·玻恩芬德（Katharina Pauernfeind）来自萨尔茨堡。他从他的家教那里接受了基础教育，而后在上奥地利的林茨就读高中。当他15岁时，他的父亲去世。

玻尔兹曼自1863年开始在维也纳大学攻读物理学。指导过他的老师有 约瑟夫·洛施密特 （ 英语 ： Johann Josef Loschmidt ） 、约瑟夫·斯特藩、安德烈亚斯·冯·厄廷格豪森和 约瑟夫·佩兹伐 （ 英语 ： Joseph Petzval ） 。玻尔兹曼在斯特藩的指导下在1866年获得理学博士学位。他的学位论文是主题是分子运动论。1867年，他成为 无俸讲师 （ 英语 ： Privatdozent ） 。在获得博士学位后，玻尔兹曼又当了两年斯特藩的助手。而正是斯特藩使玻尔兹曼了解了麦克斯韦的工作.

学术生涯

1869年，其25岁时，借助斯特藩的推荐信， 他受聘为格拉茨大学数学物理学教授。1869年，他与罗伯特·本生和 利奥·格尼斯伯格 （ 英语 ： Leo Königsberger ） 在海德尔堡共事数月，而后他1871年与古斯塔夫·基尔霍夫、赫尔曼·冯·亥姆霍兹在柏林合作过。1873年，玻尔兹曼成为维也纳大学的数学教授直至1876年。

  1887年，格拉茨，玻尔兹曼和他的共事者。（站立者，左起）瓦尔特·能斯特， 海因里希·斯特伦茨 （ 英语 ： Heinrich Streintz ） ，斯凡特·奥古斯特·阿伦尼乌斯，希尔克（Hiecke），（坐者，左起) 奥林格（Aulinger）， 阿尔伯特·冯·爱廷豪森 （ 英语 ： Albert von Ettingshausen ） ，玻尔兹曼， 伊格内修斯·克莱门季奇 （ 英语 ： Ignacij Klemenčič ） ，豪斯曼尼格（Hausmanninger）。

1872年，玻尔兹曼与格拉茨的一位有抱负的数学和物理老师亨丽埃特·艾根特拉相遇。当时奥地利的大学不录取女性，她在试图旁听当地大学讲授的课程时被拒。她在玻尔兹曼建议下进行了申诉，并获得了成功。1876年7月17日，他们结为伉俪。他们育有三个女儿和两个儿子。之后，玻尔兹曼回到格拉茨成为实验物理学教授。斯凡特·奥古斯特·阿伦尼乌斯和瓦尔特·能斯特都在格拉茨受过他的教导。 他在格拉茨度过了十四年快乐的时光。而正是在那里，他发展起他对自然界的统计概念。1885年，他成为奥地利皇家科学院院士，而后，1887年，他成为格拉茨大学的校长。1888年，他被推选为瑞典皇家科学院院士。

1890年，玻尔兹曼受聘为慕尼黑大学的理论物理学教授。1893年，他继承他的导师约瑟夫·斯特藩成为维也纳大学的理论物理学教授。

晚年

玻尔兹曼晚年投入了大量精力来捍卫他的理论。他与他在维也纳的同事交恶，特别是1895年成为哲学及科学史教授的恩斯特·马赫。同是在1895年， 格奥尔格·亥姆 （ 英语 ： Georg Helm ） 和威廉·奥斯特瓦尔德在吕贝克的一次学术会议上提出了“活力说”。他们认为能量，而非物质，是宇宙的主要组分。玻尔兹曼及支持他原子理论的物理学家与之进行了旷日持久的争论。 1900年，玻尔兹曼受威廉·奥斯特瓦尔德之邀来到莱比锡大学 在马赫因为健康状况欠佳而退休之后，1902年，玻尔兹曼回到了维也纳。 1903年，他与 古斯塔夫·冯·埃舍里希 （ 英语 ： Gustav von Escherich ） 及 埃米尔·穆勒 （ 英语 ： Emil Müller (mathematician) ） 一起创建了 奥地利数学学会 （ 英语 ： Austrian Mathematical Society ） 。他在维也纳的学生包括 卡尔·普里布拉姆 （ 英语 ： Karl Přibram ） ，保罗·埃伦费斯特和莉泽·迈特纳。

在维也纳，玻尔兹曼教授物理学，同时也讲授哲学。他关于自然哲学的演讲非常受欢迎，在当时引起相当大的关注，首次演讲即大告成功。演讲在当地最大的报告厅举行，可报告厅内依旧人满为患，以至楼梯上都站满了人。由于玻尔兹曼的哲学演讲大获成功，当时的奥匈帝国皇帝也在皇宫接见了他。

玻尔兹曼晚年精神状况欠佳，情绪经常起伏不定。（与躁郁症症状类似）他自嘲式地将他变化不定的情绪归咎于他在忏悔星期二和圣灰星期三间出生的缘故。 迈特纳指出与玻尔兹曼亲近的人都能看出他有严重的抑郁和自杀倾向。

1906年9月5日，在的里雅斯特附近的 杜伊诺 （ 英语 ： Duino ） 度假时，玻尔兹曼在情绪失控中自缢身亡。 他被葬于维也纳中央公墓，他的墓碑上镌刻着玻尔兹曼熵公式:

其中 l o g {\displaystyle log} 表示自然对数。

哲学观点

玻尔兹曼的分子运动论是在预设原子和分子确实存在前提下建立的。但当时几乎所有的德国哲学家和许多科学家，像恩斯特·马赫及物理化学家威廉·奥斯特瓦尔德，都不认为它们实际存在。十九世纪九十年代，他试图通过建立一种绕过讨论原子是否存在来折衷原子论和反原子论的立场。他的解决方法是引用赫兹的理论，将原子仅仅归为一种物理模型——原子论者可以认为这个模型就是实实在在的原子，而反原子论者可以认为原子是一个有用但并非实际存在的模型。但这并没有使双方满意。而由于玻尔兹曼对于原子和分子存在的假定及对热力学第二定律统计意义上的解释，奥斯特瓦尔德及众多“纯粹热力学”的拥护者更进一步试图去否定分子运动论和统计力学的合理性。

而在世纪之交，玻尔兹曼的科学工作受到一个新兴思潮的威胁。一些物理学家，包括马赫的学生， 古斯塔夫·焦曼 （ 英语 ： Gustav Jaumann ） ，认为赫兹的理论中的所有的电磁现象都是连续变化的，而所有的物理现象最终都可以还原为电磁现象。由于原子和分子的存在会破坏这种连续性，因而它们并不存在。这一思潮深深打击了玻尔兹曼，因为它可能意味着他的分子运动论及对热力学第二定律统计意释的终结。

而1901年，马赫离职后， 玻尔兹曼重返维也纳，并决定自己从哲学意义上来解释自己的物理学理论来应对对其的质疑，但不久又再次受挫。1904年，在圣路易斯举办的一个物理学会议上，与会的大多数物理学家否定原子的存在。他没有受邀参加物理学部分的讨论，更在应用数学部分讨论受阻。他认为对于科学家来说，去克服从过去继承来的哲学理念是非常困难的。

1905年，玻尔兹曼试图通过与弗朗兹·布伦塔诺的广泛交流来进一步理解哲学的本质以使科学摆脱它的影响，但他本人也对这个想法没有什么信心。1906年，他的精神状态已经糟糕到他不得不离职。当年9月他在与他妻子及女儿在意大利的的里亚斯特度假时自缢身亡。

物理学成就

玻尔兹曼最重要的科学方面的贡献是分子运动论，其中包括研究气体分子运动速度的麦克斯韦-玻尔兹曼分布，基于经典力学的研究能量的麦克斯韦-玻尔兹曼统计和玻尔兹曼分布。它们能在非必须量子统计时解释许多现象，并且更深入的揭示了温度等热力学系统的状态函数的物理意义。

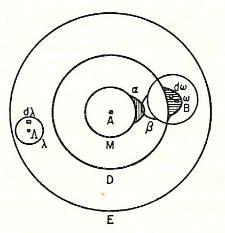
  1898年玻尔兹曼所作碘分子的图示，其中原子“敏感区域”α和β发生重叠。

当时多数物理学家并不像他一样深信原子和分子的切实存在。而苏格兰的詹姆斯·克拉克·麦克斯韦和美国的约西亚·吉布斯，以及自约翰·道尔顿1808提出原子论来的大多数化学家却深信原子和分子的存在。玻尔兹曼和当时德国首级的物理学刊物的编辑进行了旷日持久的争论。这些编辑只是将原子和分子当作方便的理论模型而并不愿将它们与现实联系起来。在玻尔兹曼去世后数年，让·佩兰在阿尔伯特·爱因斯坦1905年的研究基础上对于胶体悬浮物的研究（1908–1909），测定了阿伏伽德罗常量和玻尔兹曼常数，并向世界证明了原子和分子确实存在。

玻尔兹曼还在分子运动论中发现了熵和微观状态的概率分布的对数关系， 并提出著名的玻尔兹曼熵公式 ：

其中 k = 1.3806505(24) × 10 J |K ，称作玻尔兹曼常数。 W {\displaystyle W} 是德语中概率（ Wahrscheinlichkeit ）的缩写， ，这里，更准确地说，是系统的微观状态数。玻尔兹曼的范式是有 N 个分子的理想气体， N i 是分子位置和动量的第 i 个微观状态。 W {\displaystyle W} 可以用下面这个排列式计算：

其中 i 的范围是分子所有可能的微观状态。 由于系统中相同状态的相同粒子是不可区别的，因而对分母进行了“修正”。

玻尔兹曼由于他在1877年暗示一个物理学系统的能级离散成为量子力学的先驱。

玻尔兹曼熵公式被镌刻在他维也纳中央墓地的墓碑上。

玻尔兹曼方程

  维也纳大学主楼院子拱廊中的玻尔兹曼胸像

玻尔兹曼方程叙述了理想气体系统内部粒子的运动情况。

其中 ƒ 为分布函数（参见麦克斯韦-玻尔兹曼分布），代表在某一时刻在一位置和具有该动量的粒子数目、密度或发现粒子的概率， F 是力(包含相对于所讨论系统的外力与粒子之间的相互作用)， m 是单个粒子的质量， t 是时间， v 是具有该动量粒子所拥有的速度。

这个方程描述了粒子位置和动量概率分布在相空间中的密度分布云图随时间和空间的演化（参见哈密尔顿力学）。等式左边第一项代表分布函数随时间的变化，第二项给出随空间的变化，然后第三项描述了某个力对粒子的影响效果。等式右边代表碰撞（collision）的所造成的分布函数的变化(如交换动量或能量)。

从原理上，在适当的边界条件下，这个方程可以描述气体粒子集合体的动态。 这个一阶偏微分方程看起来非常易解， 因为 ƒ 可以表示任意的单粒子分布函数，并且作用在粒子上的力直接取决于速度分布函数，但却以难以积分著称。大卫·希尔伯特多年努力去解它但却没有获得实质成功。

由玻尔兹曼给出的表示碰撞的项是近似的。但玻尔兹曼方程对于理想气体的恰普曼一恩斯科格（Chapman–Enskog）解却是高度严格的。只有在激波条件下，才有可能得到对于理想气体的错误的解。

玻尔兹曼使用许多年试图利用这个方程证明H定理进而验证热力学第二定律。这之中他做了一个假设——碰撞的项是针对分子混沌的。然而这个假设破坏了时间反演对称，暗示了第二定律的必然成立。所以他在与洛施密特以及其他基于洛施密特佯谬的观点的长期争论中落败。

而在20世纪70年代，E.G.D. Cohen和J.R. Dorfman证明了玻尔兹曼方程对于高密度物质的系统扩展在数学上是不可能的。最终对于稠密气体及液体的非平衡态的统计力学研究焦点已经转移到格林-久保关系（Green-Kubo relations）,涨落定理及其他方法。

对热力学第二定律的阐释

  玻尔兹曼之墓，在他的墓碑上镌刻着熵公式

现在认为热力学第二定律是描述系统无序性的定律的观点源于玻尔兹曼对其的理解。而他亦试图将其还原为描述机械粒子间随机碰撞概率的定律。玻尔兹曼沿用麦克斯韦的方法 也将气体分子模型化为箱中相互碰撞的台球，而随着分子间的碰撞，速度分布会变得更为无序，最终导致了系统的宏观性质均一，而微观处于最为无序的状态，或者说系统的熵趋于最大值。 由此他提出热力学第二定律是微观世界的最概然状态为无序在宏观的表现。之所以微观世界的最概然状态（即最可能处于的状态）是无序态，是由于无序的微观状态数远多于有序的微观状态数。玻尔兹曼总结道，分子“以同样的速率在同一方向”运动的有序状态“，可以想象，是最不可能处于的状态，亦是不可能的能量组态。”

玻尔兹曼将热力学第二定律归结为统计现象的这一功绩使热力学中的熵增加原理得到统计上的解释从而更易理解。

另见

以维希·玻尔兹曼命名的事物列表

能量均分定理

玻尔兹曼大脑

玻尔兹曼模型

分子理论史

计算流体力学的格子玻尔兹曼法（Lattice Boltzmann methods (LBM)）

热学统计力学哲学

维希·玻尔兹曼协会

玻尔兹曼奖

玻尔兹曼（陨石坑）

延伸阅读

Roman Sexl & John Blackmore (eds.), "Ludwig Boltzmann – Ausgewahlte Abhandlungen", (Ludwig Boltzmann Gesamtausgabe, Band 8), Vieweg, Braunschweig, 1982.

John Blackmore (ed.), "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book One: A Documentary History", Kluwer, 1995. ISBN 978-0-7923-3231-2

John Blackmore, "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book Two: The Philosopher", Kluwer, Dordrecht, Netherlands, 1995. ISBN 978-0-7923-3464-4

John Blackmore (ed.), "Ludwig Boltzmann – Troubled Genius as Philosopher", in Synthese, Volume 119, Nos. 1 & 2, 1999, pp. 1–232.

Brush, Stephen G. (ed. & tr.), Boltzmann, Lectures on Gas Theory , Berkeley, CA: U. of California Press, 1964

Brush, Stephen G. (ed.), Kinetic Theory , New York: Pergamon Press, 1965

ISBN 9780198501541 单击这里添加你的引用。 如果你仍在编辑主页面文章，你可能需要在一个新窗口打开。

Boltzmann, Ludwig Boltzmann – Leben und Briefe , ed., Walter Hoeflechner, Akademische Druck- u. Verlagsanstalt. Graz, Oesterreich, 1994

Brush, Stephen G. Boltzmann. (编) Charles Coulston Gillispie (ed.). Dictionary of Scientific Biography. New York: Scribner. 1970. ISBN 0-684-16962-2.

Brush, Stephen G. The Kind of Motion We Call Heat: A History of the Kinetic Theory of Gases. Amsterdam: North-Holland. 1986. ISBN 0-7204-0370-7.

Everdell, William R. The Problem of Continuity and the Origins of Modernism: 1870–1913. History of European Ideas. 1988, 9 (5): 531–552. doi:10.1016/0191-6599(88)90001-0 .

Everdell, William R. The First Moderns. Chicago: University of Chicago Press. 1997.

P. Ehrenfest & T. Ehrenfest (1911) "Begriffliche Grundlagen der statistischen Auffassung in der Mechanik", in Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen Band IV, 2. Teil ( F. Klein and C. Müller (eds.). Leipzig: Teubner, pp. 3–90. Translated as The Conceptual Foundations of the Statistical Approach in Mechanics . New York: Cornell University Press, 1959. ISBN 978-0-486-49504-0

Klein, Martin J. The Development of Boltzmann’s Statistical Ideas. (编) E.G.D. Cohen and W. Thirring (eds). The Boltzmann Equation: Theory and Applications. Acta physica Austriaca Suppl. 10. Wien: Springer. 1973: 53–106. ISBN 0-387-81137-0.

Tolman, Richard C. The Principles of Statistical Mechanics. Oxford University Press. 1938. Reprinted: Dover (1979). ISBN 978-0-486-63896-6

Gibbs, Josiah Willard. Elementary Principles in Statistical Mechanics, developed with especial reference to the rational foundation of thermodynamics. New York: Charles Scribner"s Sons. 1902.

Lindley, David. Boltzmann"s Atom: The Great Debate That Launched A Revolution In Physics. New York: Free Press. 2001. ISBN 0-684-85186-5.

Lotka, A. J. Contribution to the Energetics of Evolution. Proc. Natl. Acad. Sci. U.S.A. 1922, 8 (6): 147–51.Bibcode:1922PNAS....8..147L. PMC 1085052 . PMID 16576642 . doi:10.1073/pnas.8.6.147 .

Bronowski, Jacob. World Within World. The Ascent Of Man. Little Brown & Co. 1974. ISBN 978-0-316-10930-7.

Meyer, Stefan. Festschrift Ludwig Boltzmann gewidmet zum sechzigsten Geburtstage 20. Februar 1904. J. A. Barth. 1904 （德文） .

Planck, Max. The Theory of Heat Radiation. P. Blakiston Son & Co. 1914. English translation by Morton Masius of the 2nd ed. of Waermestrahlung . Reprinted by Dover (1959) & (1991). ISBN 978-0-486-66811-6

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。