与其它物理量的关系

对于纯电阻线路，电导 G {\displaystyle G\,\!} 与电阻 R {\displaystyle R\,\!} 的关系方程为

欧姆定律是

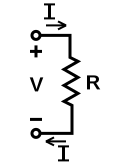
其中， V {\displaystyle V\,\!} 是电压， I {\displaystyle I\,\!} 是电流。

所以，可以得到 欧姆电导定律 的关系方程：

请注意，当阻抗是复值时，这些关系方程不成立。这时，电导与电纳 B {\displaystyle B\,\!} 和导纳 Y {\displaystyle Y\,\!} 的关系方程为

或者，

其中， j {\displaystyle j\,\!} 是虚数单位。

一个截面面积为 A {\displaystyle A\,\!} ，长度为 ℓ ℓ --> {\displaystyle \ell \,\!} 的物体，其电导 G {\displaystyle G\,\!} 可以由电导率 σ σ --> {\displaystyle \sigma \,\!} 求得：

电路等效电导的运算

从基尔霍夫电路定律，我们可以演绎电导元件的综合法则。

并联电路

给予两个并联的电导元件 G 1 {\displaystyle G_{1}\,\!} 、 G 2 {\displaystyle G_{2}\,\!} 。这两个电导元件两端的电压必相等。按照基尔霍夫电流定律，总电流 I e q {\displaystyle I_{eq}\,\!} 是

其中， I 1 {\displaystyle I_{1}\,\!} 、 I 2 {\displaystyle I_{2}\,\!} 分别为通过电导元件 G 1 {\displaystyle G_{1}\,\!} 、 G 2 {\displaystyle G_{2}\,\!} 的电流。

将欧姆电导定律的方程代入，可以得到

所以，等效电导 G e q {\displaystyle G_{eq}\,\!} 是

串联电路

给予两个串联的电导元件 G 1 {\displaystyle G_{1}\,\!} 、 G 2 {\displaystyle G_{2}\,\!} 。通过这两个电导元件的电流必相等。按照基尔霍夫电压定律，总电压 V e q {\displaystyle V_{eq}\,\!} 等于两个电导元件两端的电压 V 1 {\displaystyle V_{1}\,\!} 、 V 2 {\displaystyle V_{2}\,\!} 的总和：

将欧姆电导定律的方程代入，可以得到

所以，等效电导 G e q {\displaystyle G_{eq}\,\!} 是

重新编排，

小信号元件电导

我们可以应用电导于电子元件，像晶体管或二极管。通常，我们会采用小信号模型（ small-signal model ），在一个给定的直流操作点，称为Q-点（ Q-point ），相关的元件方程会被线形化。所得到的小信号元件电阻的倒数，就是小信号元件电导。若想知道更详细资料，请参阅尔利效应。

参考文献

Halliday, David; Robert Resnick, Jearl Walker. Fundamental of Physics 7th. USA: John Wiley and Sons, Inc. 2005. ISBN 0-471-23231-9.

参阅

西门子 (单位)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。