历史

  杨辉三角形

二项式系数的三角形排列通常被认为是法国数学家布莱兹·帕斯卡的贡献，他在17世纪描述了这一现象 。但早在他之前，就曾有数学家进行类似的研究。例如，古希腊数学家欧几里得于公元前4世纪提到了指数为2的情况 。公元前三世纪，印度数学家青目探讨了更高阶的情况。帕斯卡三角形的雏形于10世纪由印度数学家大力罗摩发现。在同一时期，波斯数学家 卡拉吉 （ 英语 ： Al-Karaji ） 和数学家兼诗人欧玛尔·海亚姆得到了更为普遍的二项式定理的形式。13世纪，中国数学家杨辉也得到了类似的结果 。 卡拉吉 （ 英语 ： Al-Karaji ） 用数学归纳法的原始形式给出了二项式定理和帕斯卡三角形(巴斯卡三角形)的有关证明 。艾萨克·牛顿勋爵将二项式定理的系数推广到有理数 。

定理的陈述

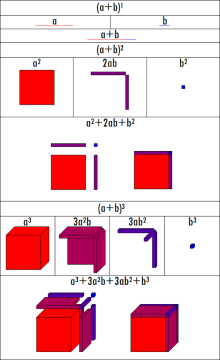
  以几何的方式解释二项式定理

根据此定理，可以将 x + y 的任意次幂展开成和的形式

其中每个 ( n k ) {\displaystyle {\tbinom {n}{k}}} 为一个称作二项式系数的特定正整数，其等于 n ! k ! ( n − − --> k ) ! {\displaystyle {\frac {n!}{k!(n-k)!}}} 。这个公式也称 二项式公式 或 二项恒等式 求和符号和符号，可以把它写作

后面的表达式只是将根据 x 与 y 的对称性得出的，通过比较发现公式中的二项式系数也是对称的。 二项式定理的一个变形是用 1 来代换 y 得到的，所以它只涉及一个变量。在这种形式中，公式写作

或者等价地

证明

数学归纳法

当 n = 1 {\displaystyle n=1} ，

假设二项展开式在 n = m {\displaystyle n=m} 时成立。若 n = m + 1 {\displaystyle n=m+1} ，

组合方法

考虑 ( a + b ) 7 = ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) {\displaystyle (a+b)^{7}=(a+b)(a+b)(a+b)(a+b)(a+b)(a+b)(a+b)} ，共7个括号相乘，从7个括号选出其中的4个括号中的 a ，再从剩余的3个括号中选出3个 b 相乘，便得一组 a 4 b 3 {\displaystyle a^{4}b^{3}} ，而这样的选法共有 ( 7 4 ) {\displaystyle {\tbinom {7}{4}}} 种，故总共有 ( 7 4 ) {\displaystyle {\tbinom {7}{4}}} 个 a 4 b 3 {\displaystyle a^{4}b^{3}} ；其他各项同理。

同理， ( a + b ) n = ( a + b ) ( a + b ) . . . . ( a + b ) ( a + b ) {\displaystyle (a+b)^{n}=(a+b)(a+b)....(a+b)(a+b)} ，共 n 个括号相乘，从 n 个括号选出其中的 k 个括号中的 a ，再从剩余的( n - k )个括号中选出( n - k )个 b 相乘，便得一组 a k b n − − --> k {\displaystyle a^{k}b^{n-k}} ，而这样的选法共有 ( n k ) {\displaystyle {\tbinom {n}{k}}} 种，故总共有 ( n k ) {\displaystyle {\tbinom {n}{k}}} 个 a k b n − − --> k {\displaystyle a^{k}b^{n-k}} ；其他各项同理。

不尽相异物排列方法

考虑 ( a + b ) 7 = ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) ( a + b ) {\displaystyle (a+b)^{7}=(a+b)(a+b)(a+b)(a+b)(a+b)(a+b)(a+b)} ，每一个括号可以出 a 或出 b ，而最后要有4个 a 、3个 b 相乘，这形同 aaaabbb 的“不尽相异物排列”，其方法数为 7 ! 4 ! × × --> 3 ! {\displaystyle {\frac {7!}{4!\times 3!}}} ，恰好等于 ( 7 4 ) {\displaystyle {\tbinom {7}{4}}} ；其他各项同理。

同理， ( a + b ) n = ( a + b ) ( a + b ) . . . . ( a + b ) ( a + b ) {\displaystyle (a+b)^{n}=(a+b)(a+b)....(a+b)(a+b)} ，每一个括号可以出 a 或出 b ，而最后要有 k 个 a 、( n - k )个 b 相乘，这形同 aa....aabb....bb 的“不尽相异物排列”，其方法数为 n ! k ! × × --> ( n − − --> k ) ! {\displaystyle {\frac {n!}{k!\times (n-k)!}}} ，恰好等于 ( n k ) {\displaystyle {\tbinom {n}{k}}} ；其他各项同理。

一般形式的证明

通常二项式定理可以直接使用泰勒公式进行证明. 下面的方法不使用泰勒公式

因为 ∑ ∑ --> k = 0 ∞ ∞ --> ( a k ) k x k = ( a 0 ) ⋅ ⋅ --> 0 x 0 + ∑ ∑ --> k = 1 ∞ ∞ --> ( a k ) k x k = ∑ ∑ --> k = 1 ∞ ∞ --> ( a k ) k x k {\displaystyle \sum _{k=0}^{\infty }{a \choose k}kx^{k}={a \choose 0}\cdot 0x^{0}+\sum _{k=1}^{\infty }{a \choose k}kx^{k}=\sum _{k=1}^{\infty }{a \choose k}kx^{k}}

根据除法定则， d d x ( g ( x ) f ( x ) ) = g ′ ( x ) f ( x ) − − --> f ′ ( x ) g ( x ) ( f ( x ) ) 2 = 0 {\displaystyle {\frac {d}{dx}}\left({\frac {g(x)}{f(x)}}\right)={\frac {g"(x)f(x)-f"(x)g(x)}{(f(x))^{2}}}=0}

根据拉格朗日中值定理， g ( x ) f ( x ) {\displaystyle {\frac {g(x)}{f(x)}}} 是常数函数.

应用

牛顿以二项式定理作为基石发明出了微积分 。其在初等数学中应用主要在于一些粗略的分析和估计以及证明恒等式等。

证明组合恒等式

二项式定理给出的系数可以视为组合数 ( n k ) {\displaystyle {n \choose k}} 的另一种定义。 因此二项式展开与组合数的关系十分密切。 它常常用来证明一些组合恒等式。比如证明 ∑ ∑ --> k = 0 n ( n k ) 2 = ( 2 n n ) {\displaystyle \sum _{k=0}^{n}{n \choose k}^{2}={2n \choose n}}

可以考虑恒等式 ( 1 + x ) n ( 1 + x ) n = ( 1 + x ) 2 n {\displaystyle (1+x)^{n}(1+x)^{n}=(1+x)^{2n}} 。 展开等式左边得到： ∑ ∑ --> i = 0 n ∑ ∑ --> j = 0 n ( n i ) ( n j ) x i x j {\displaystyle \sum _{i=0}^{n}\sum _{j=0}^{n}{n \choose i}{n \choose j}x^{i}x^{j}} 。 注意这一步使用了有限求和与乘积可以交换的性质。 同时如果展开等式右边可以得到 ∑ ∑ --> k = 0 2 n ( 2 n k ) x k {\displaystyle \sum _{k=0}^{2n}{2n \choose k}x^{k}} 。 比较两边幂次为 k {\displaystyle k} 的项的系数可以得到: ∑ ∑ --> i = 0 k ( n i ) ( n k − − --> i ) = ( 2 n k ) {\displaystyle \sum _{i=0}^{k}{n \choose i}{n \choose k-i}={2n \choose k}} 。 令 k = n {\displaystyle k=n} ，并注意到 ( n i ) = ( n n − − --> i ) {\displaystyle {n \choose i}={n \choose n-i}} 即可得到所要证明的结论。

多倍角恒等式

在复数中，二项式定理可以与棣莫弗公式结合，成为多倍角公式 。根据棣莫弗公式：

通过使用二项式定理，右边的表达式可以扩展为

由棣莫弗公式，实部与虚部对应，能够得出

即二倍角公式。同样，因为

所以藉棣莫弗公式，能够得出

整体而言，多倍角恒等式可以写作

和

e级数

数学常数e的定义为下列极限值：

使用二项式定理能得出

第 k 项之总和为

因为 n → ∞，右边的表达式趋近1。因此

这表明e可以表示为

推广

该定理可以推广到对任意实数次幂的展开，即所谓的牛顿 广义二项式定理 ：

( x + y ) α α --> = ∑ ∑ --> k = 0 ∞ ∞ --> ( α α --> k ) x α α --> − − --> k y k {\displaystyle (x+y)^{\alpha }=\sum _{k=0}^{\infty }{\alpha \choose k}x^{\alpha -k}y^{k}} 。其中 ( α α --> k ) = α α --> ( α α --> − − --> 1 ) . . . ( α α --> − − --> k + 1 ) k ! = ( α α --> ) k k ! {\displaystyle {\alpha \choose k}={\frac {\alpha (\alpha -1)...(\alpha -k+1)}{k!}}={\frac {(\alpha )_{k}}{k!}}} 。

多项式展开

对于多元形式的多项式展开，可以看做二项式定理的推广： ( x 1 + x 2 + . . . + x n ) k = ∑ ∑ --> α α --> 1 + α α --> 2 + . . . + α α --> n = k k ! α α --> 1 ! . . . α α --> n ! x 1 α α --> 1 . . . x n α α --> n {\displaystyle \left(x_{1}+x_{2}+...+x_{n}\right)^{k}=\sum _{\alpha _{1}+\alpha _{2}+...+\alpha _{n}=k}{\frac {k!}{\alpha _{1}!...\alpha _{n}!}}x_{1}^{\alpha _{1}}...x_{n}^{\alpha _{n}}} .

证明：

数学归纳法。对元数n做归纳： 当n=2时，原式为二项式定理，成立。 假设对n-1元成立，则：

参见

二项分布

组合

立方根

平方根

牛顿法

多项式定理

负二项分布

杨辉三角形

斯特灵公式

参考书目

Bag, Amulya Kumar. Binomial theorem in ancient India. Indian J. History Sci. 1966, 1 (1): 68–74.

Barth, Nils R. (November 2004). "Computing Cavalieri"s Quadrature Formula by a Symmetry of the n-Cube". The American Mathematical Monthly (Mathematical Association of America) 111 (9): 811–813. doi:10.2307/4145193. ISSN 0002-9890. JSTOR 4145193,author"s copy,further remarks and resources

Graham, Ronald; Knuth, Donald; Patashnik, Oren. (5) Binomial Coefficients. Concrete Mathematics 2nd. Addison Wesley. 1994: 153–256. ISBN 0-201-55802-5. OCLC 17649857 .

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。