概述

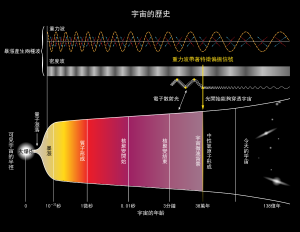
 宇宙的历史。根据推测，大爆炸刚发生后的超光速暴涨过程产生了引力波 。

爱因斯坦广义相对论所描述的引力，是时空曲率所产生的一种现象。质量可以导致这种曲率。当物质在时空中运动时，附近的曲率就会随之改变。大质量物体运动时所产生的曲率变化会以光速像波一样向外传播。这一传播现象就是引力波 。

当引力波通过远处的观测者时，观测者会发现时空被扭曲了。两个自由物体之间的距离会有节奏地波动，频率与引力波相同。然而，在这一过程中，这两个自由物体并没有受力，坐标位置也没有变化；改变的，是时空坐标本身的距离。在观测者处的引力波强度和与波源间的距离呈反比。 根据预测，螺旋形靠近的中子双星系统由于质量高、加速度高，因此在合并时会发射出强大的引力波。但是因为天文距离尺度之大，就算是最激烈的事件所产生的引力波，在到达地球后效应已变得极低，其应变的数量级低于10 。为了探测到这种细微的变化，科学家不断增加探测器的灵敏度。截至2012年 ( 2012-Missing required parameter 1= month ! ) ，最为敏感的探测器位于LIGO和VIRGO天文台，灵敏度高达 5 × 10 。这些天文台未能探测到引力波，这为这种引力波的频率设下了上限 。欧洲空间局正在研发一座用来探测引力波的空间天文台，激光干涉空间天线 。

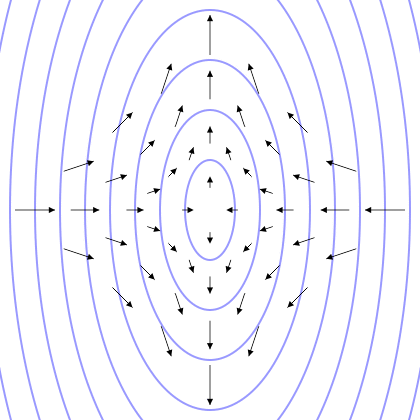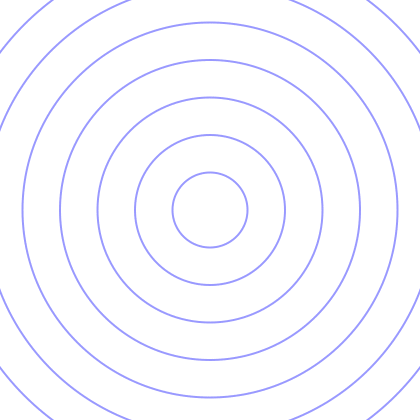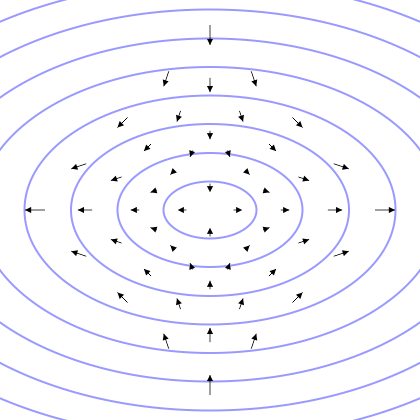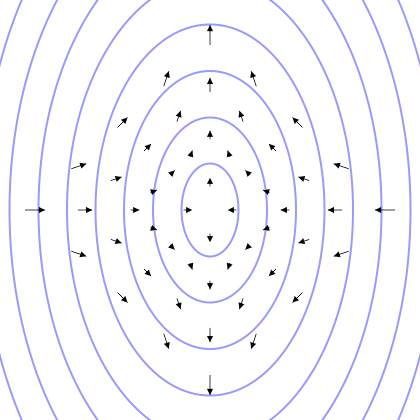
  线性偏振引力波

引力波能够穿透电磁波所无法穿透的空间。科学家推测，引力波能够帮助了解位于宇宙远处的各种天体，例如黑洞。这类天体无法用光学望远镜和射电望远镜等传统方式观测。宇宙学家还能够利用引力波来观测宇宙最早期状态。传统的天文学方法无法用来直接观测早期宇宙，因为在复合之前，宇宙无法被电磁波所穿透 。对引力波更精确的测量还能进一步验证广义相对论 。

引力波理论上可以取任何频率，但极低频率几乎无法探测，而极高频率也没有可观测的已知波源。史蒂芬·霍金和维尔纳·伊斯雷尔（ Werner Israel ）预测，可以被探测到的引力波频率在10 Hz和10 Hz之间 。

引力波通过时的效应

  一个由粒子组成的环在十字型偏振引力波下的作用

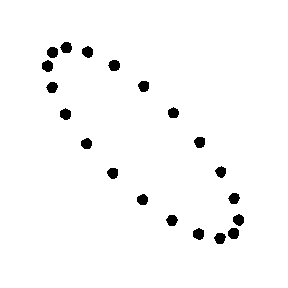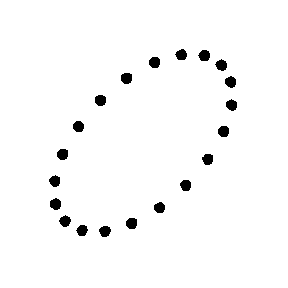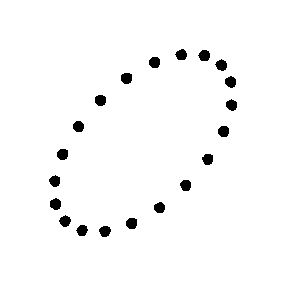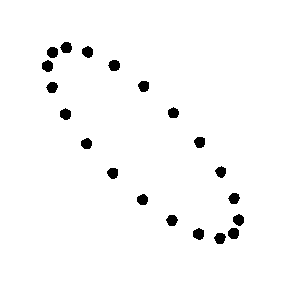
  一个由粒子组成的环在交叉型偏振引力波下的作用

要了解引力波通过观测者时的作用，可以想像一个完全平坦的时空区域，里面有一组静止的试验粒子形成一个平面。当引力波沿着垂直于该平面的方向通过这些粒子的时候，它们就会随着扭曲了的时空而“十字形”摆动（见右边动画）。试验粒子所包围之面积不变，而且粒子不会沿波传播的方向运动 。当横向粒子距离最大时，纵向的粒子距离就最小；相反，横向离子距离最小时，纵向粒子距离就最大 。

动画大大夸大了粒子的摆动，引力波的振幅实际上是非常小的。两个质量互相作圆周轨道运动，就可以产生这种效果。在这种情况下，引力波的振幅不变，但其偏振平面会以公转周期的两倍旋转。所以引力波大小（周期性时空应变）会随时间改变，如动画所示 。如果轨道呈椭圆形，则振幅本身也会随时间变化。

正如其他波一样，引力波也有几项特征属性：

振幅 ：通常记作 h ，描述波大小的一个无量纲量，是两个粒子间距离的最大挤压度占原距离的比例 。动画中的振幅大约为 h =0.5。两个黑洞合并时所产生的引力波在通过地球时，振幅只有 h ~10 。

频率：通常记作 f ，波振动的频率（1除以两次最大挤压之间的时间间隔）。

波长：通常记作 λ ，波的两个最大挤压处之间的空间间隔。

速度：波传播的速度。在广义相对论中，引力波以光速 c 传播 。

从这些量可以算出，引力波的光度为一个关于四极矩的三阶时间导数的函数 。

引力波的速度、波长和频率之间的关系为 c = λ f ，这与电磁波的对应方程相同。例如，动画中的粒子大约每2秒摆动一次，即频率为0.5 Hz，波长约为600,000 km，即大约地球直径的47倍。

以上例子假设了波具有“十字型”线性偏振，记作 h + {\displaystyle h_{+}} 。和光波的偏振不同的是，引力波的偏振之间呈45度角，而非90度。如果偏振为“交叉型” h × × --> {\displaystyle h_{\times }} ，那么试验粒子的波动十分相似，只是方向旋转了45度，正如第二幅动画所示。和光波一样，引力波偏振还可以以圆偏振波表示。引力波的偏振取决于波源的性质和角度 。

振幅上限的估算

一个典型系统的四极矩分量 Q i j {\displaystyle Q_{ij}} 具有 M R 2 {\displaystyle MR^{2}} 的量级，这里 M 是系统的质量， R 是系统的尺寸半径，因此可以认为这一分量对时间的二阶导数具有 M v 2 {\displaystyle Mv^{2}} 的量级，其中 v 2 {\displaystyle v^{2}} 是系统内部引起引力辐射的运动速度的平方。则代入四极矩公式可得辐射的引力波强度为：

注意到这里 M r {\displaystyle {\frac {M}{r}}} 就是波源外部距离为 r 处的牛顿引力势，引力波强度与外部引力势 ϕ ϕ --> e x t {\displaystyle \phi _{ext}} 的比值 ϵ ϵ --> {\displaystyle \epsilon } 为

根据自引力系统的位力定理，这个比值不能大于波源内部牛顿引力势的最大值 ϕ ϕ --> i n t {\displaystyle \phi _{int}} 。这样得到了一个很方便实用的估算引力波振幅上限的方法。 对于一个在室女座星系团内放出引力辐射的中子星，可估算出其引力辐射的上限为5×10 。几十年来，科学家都利用这种方法引力波探测器探测器灵敏度的最低要求 。

频率上限的估算

对某些特殊的引力波源而言，其引力辐射频率是受波源运动直接制约的，例如一个自转的脉冲星的引力辐射频率是其自转频率的两倍 。但对大多数双星系统，引力辐射频率和其自然频率相关，自然频率定义为

这里 ρ ρ --> ¯ ¯ --> {\displaystyle {\bar {\rho }}} 是波源的能量-质量的平均密度。对双星系统这个频率和其轨道频率有相同的数量级。

很显然波源的质量 M 和尺寸半径 R 决定了它的自然频率，对球体而言有 ρ ρ --> ¯ ¯ --> = 3 M 4 π π --> R 3 {\displaystyle {\bar {\rho }}={\frac {3M}{4\pi R^{3}}}} 。对太阳质量为1.4倍太阳质量，半径为10千米的中子星，其赫兹频率为1.9千赫兹；对一个质量为10倍太阳质量，视界半径为30千米的黑洞，其自然频率为1千赫兹；而对于质量为2.5×10 倍太阳质量，位于银河系中心的超大质量黑洞，其自然频率为4毫赫兹，因为其密度反而更低 。从自然频率估计的引力辐射频率一般来说在数量级上是正确的，本质上是一个快捷但很粗略的估计，得到是其真实频率的上限 。

引力波源

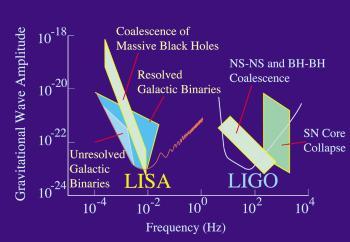
  LIGO和LISA主要探测的波源频域分布。横轴为频率，纵轴为引力波振幅。

引力波的产生，是因为非对称的运动造成了四极矩随时间变化。笼统的说法是，只要一个系统在运动时轮廓变化了，就能够生成引力波。例如，一支铅笔的旋转会否产生引力波，要看其旋转轴：沿着铅笔则无，垂直于铅笔则有 。另一个简单的例子是哑铃的旋转。如果哑铃的两端好像两个天体互相公转（即旋转轴垂直于连接哑铃两端的把手），它就会产生引力波。如果哑铃的两端质量极高，就可以模拟中子星或黑洞双星系统 。非对称系统的质量越高，运动速度越高，其散发的引力波就会越强 。

引力波的频率取决于动态系统的特征时间尺度。对于双星系统，两个天体相互公转的频率就是引力波的频率。引力波源一般以频带分类。1至10 kHz的归为高频波源，来自于中子双星、双黑洞、超新星等等，这一频率段在地基引力波探测器的侦测精度范围以内。1 mHz至1 Hz的归为低频波源，来自于特大质量黑洞、矮双星、白矮双星等等，能用空间激光干涉仪和航天器多普勒跟踪方法来侦测。1 nHz至1 mHz的归为甚低频波源，来自于特大质量黑洞、宇宙弦尖点（cosmic string cusp）等等，这是脉冲星计时实验所研究的频带。最后10 至10 Hz的归为极低频波源，对应于宇宙微波背景中所能探测到的引力波特征 。

双星系统

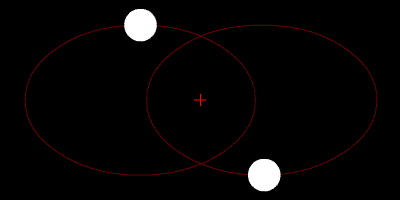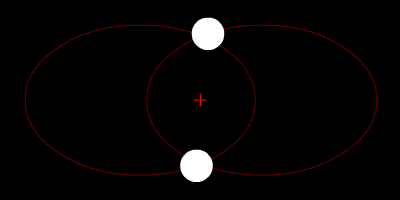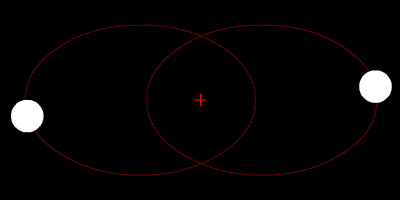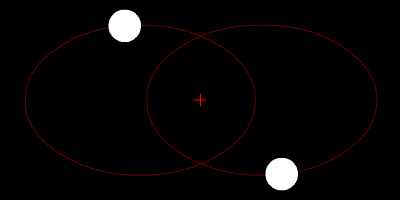
  双星系统绕质心运动的示意图，在牛顿力学中这个轨道总是稳定的，但在相对论力学下引力辐射会造成轨道的缓慢收缩

能够辐射可观测量级引力波的密近双星系统包括白矮星、中子星和黑洞等致密恒星组成的双星系统，例如黑洞双星、黑洞-中子星、双中子星、双白矮星等等。它们具有很大且随时间变化的四极矩，对LIGO等地面探测器和空间探测器LISA而言都是重要的引力波源，也是至今唯一由间接观测证实的引力波源（脉冲双星系统PSR 1913+16）。从总体上看，双星系统的引力辐射过程实际是一个双星逐渐接近结合的过程，这一过程按顺序分为旋近、合并、自转减缓三相 。

引力辐射会使在旋近态中的双星损失动能，造成其轨道以很缓慢的速度发生衰减，两颗恒星逐渐接近。换句话说，它们发生引力辐射的时间尺度远大于其公转周期，因此这一过程被认为是绝热的，最常用的预测波形的方法是后牛顿近似方法 。从引力波的频率估算方法可知，双星系统的辐射频率与其自身密度的平方根成正比关系。地面探测器可探测的双星包括中子星和恒星质量黑洞，LISA则负责探测白矮星等未知双星和超大质量黑洞 。

轨道运动辐射的能量会造成轨道的收缩，其结果是观测到发射的引力波频率随时间增长，这种波叫做啁啾（chirp）信号。如果能够观测到啁啾的时间尺度，就可以推算出双星的啁啾质量 ；进而可以从啁啾质量和观测到的引力波振幅推算出双星到地球的距离，这意味着将有可能进一步借此测量哈勃常数和其他宇宙学常数 。

随着双星系统的轨道衰减逐渐加快，绝热近似不再适用，这样双星系统进入合并态：两颗恒星接近后发生猛烈的接触合并成一个黑洞，并有相当部分的质量以引力波的形式释放（但也有很大一部分质量由于角动量守恒的制约无法离开黑洞视界，从而在黑洞附近形成吸积盘，一般说法认为这有可能会导致伽玛射线暴的形成），这里后牛顿近似方法不适用（参见恒星质量黑洞一节）；这个合并形成的黑洞随后进入自转减缓态，随着引力辐射黑洞的自转频率逐渐降低，最后稳定成一个克尔黑洞 。

本质上，双中子星在宇宙中的数量相对稀少，在可观测的范围内它们的数量要少于中子星-白矮星组成的双星系统，更少于宇宙中广泛存在的低频（10 至10 Hz）的双白矮星系统 。这些双白矮星在数量上和寿命上都要远大于像PSR B1913+16这样处于轨道收缩态的双中子星。这是由于大多数恒星都具有较小的质量，而大多数恒星又都是双星。据估计，LISA有可能发现上千个这样的双白矮星系统，其发现概率远大于地面探测器对双中子星的探测期望。不过事实上，银河系内太多的双白矮星系统会形成频率低于1毫赫兹的背景噪声，这种背景噪声叫做“迷惑噪声”，它将高于LISA本身的仪器噪声 ，但这些噪声不会影响对较强的黑洞信号的探测。而河外星系的双白矮星则由于振幅太低，尽管也能够形成高至1赫兹频率的背景噪声，其程度仍然远在LISA的仪器噪声之下 。

脉冲星

  蟹状星云，蓝色部分为钱德拉X射线天文台拍摄的X射线图像，红色部分为可见光图像，其星云中心附近存在一颗年轻的脉冲星PSR J0534+2200，极有可能会被证实为引力波源的天体之一。

对于一颗独立自转的中子星（脉冲星）而言，要成为引力波射源，其质量（或质量流）分布必须存在不对称性。非对称性的来源机制包括两类。

第一种情形是相对于星体固定的非对称性，可能的机制包括：

星体本身即是非完全对称的类球体（例如球状星团Terzan 5内部的脉冲星PSR J1748-2446ad，自转频率716赫兹，是已知自转最快的脉冲星 ）

脉冲星的磁场方向与其自转轴方向不一致（例如PSR 1828-11）

恒星吸积导致的非对称性（典型例子即低质量X射线双星，例如天鹅座X-1）

现在一般认为中子星的壳层不足以支持质量超过10 倍太阳质量的非对称性。例如，根据估算，LIGO的预期波源PSR J2124-3358的非对称性上限占总质量的1.1×10 。从这一点估算出的自转减慢态的时间尺度比实际长得太多。因此看来引力辐射并不足以成为中子星自转减慢的主要原因。以蟹状星云内部的年轻脉冲星PSR J0534+2200为例，其非对称性小于总质量的3×10 ，引力波的振幅上限约为6×10 ；而对于较老的毫秒脉冲星，非对称性只有总质量的10 左右，如果距离地球1秒差距，估算得到的振幅上限量级为10 。虽然这些典型的振幅都远低于LIGO的灵敏度，但只要长时间进行测量，就可以找到其对应的相关信号 。

第二种情形是非对称的部分相对于星体是运动的，典型的例子即是中子星r模式的不稳定性，也被称作中子星上的罗斯比波（Rossby Wave），这个名称来源于其机制类似于地球表面的科里奥利力。这种情形下，理论计算所得的引力辐射频率为自转频率的4/3倍 。

引力坍缩和伽玛射线暴

中子星的形成来源于超新星的引力坍缩，超新星内核的坍缩速率可达每秒七万千米 。这种引力坍缩并不是高度对称的，这一点已经在对超新星SN 1987A的观测中得到证实 。因此这种引力坍缩会产生一种持续时间很短且无周期性的引力波突发信号，并伴随电子捕获和中微子输运的过程 。但引力辐射的波形和振幅都很难从理论上预测，一般认为只能运用数值模拟的方法 。这种突发信号的频带可能很宽，中心频率在1千赫兹；或者有可能是在100赫兹到10千赫兹之间任意一个频率的周期性啁啾信号。理论上估计，如果在室女座星系团之内发生超新星坍缩，而且其发射的能量要大于0.01倍太阳质量，那么现在的地面探测器就有可能观测到这类事件 。但事实上到底有多大比例的能量以辐射的方式释放出来仍然是一个未能解决的问题，现在一般认为辐射能量不会超过超新星总质量的10 ，当前的引力波探测器还没有能力探测到河外星系内的超新星爆发。这类事件在银河系内的发生概率大概有几十年一次，根据计算，来自10千秒差距外引力坍缩的引力辐射振幅约为10 ，持续时间为几个毫秒。新一代地面探测器的灵敏度应该可以达到相应的水平 。

伽玛射线暴是短时间（几毫秒至几分钟）内极高强度的伽玛射线辐射突然爆发事件，按持续时间分为长短两类。根据大多数观测所得出的结论来看，伽玛射线暴很可能是高速自转的黑洞诞生时所产生的 。果真如此的话，相对于引力坍缩来说，这种高速自转的非对称性结构会形成高度稳定的引力辐射，因而有可能在观测到其电磁辐射爆发的同时探测到相应的引力辐射 。不过这种事件应该并不多见，所以需要一个很广的观测距离（至少约3吉秒差距），以及相当比例的辐射能量。然而，2007年2月发生了一次来自仙女座星系方向的GRB 070201短伽玛射线暴，而LIGO并没有探测到引力辐射的存在 。这可能是因为GRB 070201发生地点比仙女座星系更为遥远，但也可能暗示伽玛射线暴并非源于黑洞或中子星的形成过程，而是来自如磁星这样带有极强磁场的软伽玛射线复发源 。

恒星质量黑洞

天文学家现在认识到宇宙中存在数量丰富的黑洞，根据质量可分为恒星质量黑洞和位于河外星系中心的超大质量黑洞。这两类黑洞的质量非常不同，因此它们的引力辐射的机制和频率存在很大差别：恒星质量黑洞一般具有10倍左右太阳质量，形成于红巨星或超新星爆发时内部的引力坍缩；大质量和超大质量黑洞的质量则在10 至10 倍太阳质量范围内，其形成机制至今还不十分清楚。黑洞双星的自然频率和其质量成反比 。这表明恒星质量黑洞的引力波频率在地面探测器的侦测范围内，而超大质量黑洞的引力波只能用LISA这样的空间探测器捕捉到。

  NASA超级计算机模拟得到的黑洞双星开始合并的情形

恒星质量黑洞的引力辐射一般认为来源于双星系统（其中至少有一个是黑洞）的旋近-合并-自转减缓这一系列过程 ，这和双中子星等其他双星系统的引力波辐射机制是相同的。在旋近态中，两个黑洞的距离相当远（ r ≫ ≫ --> 4 M {\displaystyle r\gg 4M} ），并以很缓慢的速度逐渐接近。这时和所有双星系统一样，后牛顿近似完全足够解决此类问题。不过当黑洞双星的距离逐渐拉近，直到其轨道缩减为最内稳定圆轨道（Innermost Stable Circular Orbit，简称ISCO）时，黑洞掉入彼此的事件视界之内，双星从旋近态向合并态转变 。这种相变完全是一种相对论性效应，因此后牛顿近似在这里完全不适用。黑洞的合并必然会伴随著引力波信号的突然发射，目前这种信号只能采用数值相对论模拟的方法来分析 ，并且有很多实际计算上的困难。而且对于质量超过50倍太阳质量的黑洞，旋近态终止时的频率是最后稳定轨道的公转频率，这个值大概只有黑洞自然频率的0.06倍，约30赫兹 。这个频率已经接近地面探测器的低频极限，即使仅是探测到此类事件也需要对波形进行一些预测，因而黑洞合并数值模拟的结果对这种引力波的探测有重要意义。合并后系统进入自转减缓态，两个黑洞的视界合并成一个，黑洞双星以类似阻尼振动的形式放出引力辐射，逐渐稳定为一个单独的克尔黑洞，此过程的时空度规可以用对克尔时空的线性微扰理论解出 。自转减缓态的一个特征是它具有在数学上为复数的自转频率，即复数频率的实部是特征频率，阻尼是阻尼因子。理论上克尔黑洞的质量和角动量完全决定了所有可能的复数频率，这些频率是离散的并且有无穷多个，统称为黑洞的准简正模式（Quasi-normal modes），而黑洞的自转则可用这些准简正模式的线性叠加来描述 。

虽然宇宙间黑洞的数量要低于中子星，但据估计在空间尺度上两个黑洞构成的双星系统数量反而要比中子星的双星系统多，主要是因为中子星的双星系统相对黑洞双星系统而言不容易形成。有说法认为球状星团是以高效率形成黑洞双星的地方 ，如果事实如此，那么宇宙间黑洞双星的数量可能会比中子星双星的数量高十倍左右。由于球状星团内部的黑洞质量大于恒星的平均质量，黑洞会逐渐向星团中心运动，在中心三体的相互作用是双星形成的主要机制 。值得注意的是，这类双星系统与球状星团的引力束缚并不强，其结果就是双星有可能脱离星团开始独立演化，其稳定时间一般在10 年之内。现在的研究对于恒星质量黑洞的合并几率还不很确定，但一般认为在15兆秒差距的范围内每年至少会发生几次 。

大质量和超大质量黑洞

 哈勃空间望远镜拍摄的双天线星系，星系的碰撞很有可能导致其中心超大质量黑洞的合并

来自大质量和超大质量黑洞（即“星系质量”）的引力辐射存在两种形式：一种是超大质量黑洞的合并，另一种情形是大质量黑洞对小质量致密天体的俘获所释放的引力辐射。两者的合并模式不同，因此所发出的引力波形、理论的预测能力以及侦测方法都有所不同。

星系合并

两个特大质量黑洞的合并，就是恒星质量黑洞合并的加强版。由于参与的质量很大，其引力辐射的频率很低，但振幅却相当高。因为有效信号振幅和黑洞质量基本成近似线性关系，在相同距离下质量为10 倍太阳质量的大质量黑洞的引力辐射振幅约为10倍太阳质量的黑洞引力辐射的10 倍（ h ~ 10 ） 。这意味着空间探测器对于这类信号会具有非常高的信噪比，无论这类波源位于宇宙间哪个角落 。现在一般认为在大多数星系中心都存在质量至少在10 倍太阳质量以上的大质量或超大质量黑洞，并有证据表明超大质量黑洞的质量与其宿主星系核的质量成正比关系。与恒星不同的是，星系之间发生碰撞的概率相当高，例如蛇夫座的星系碰撞残留物NGC 6240，当中含有两个分别来自原星系的特大质量黑洞 。在两个星系合并后，两者中心的黑洞会逐渐向新形成的星系中心漂移并最终发生碰撞，这一机制说明宇宙间超大质量黑洞合并的几率是相当高的 。

极端质量比例旋

  小质量致密天体与星系中心的大质量黑洞形成的EMRI是LISA重要的探测波源之一

特大质量黑洞与白矮星、中子星、恒星质量黑洞和中等质量黑洞等较小质量致密天体合并，这被称作极端质量比例旋（Extreme Mass Ratio Inspiral，简称EMRI）。当一个致密星体碰巧接近星系中心的超大质量黑洞时它有可能被俘获，在围绕着超大质量黑洞公转的同时放出引力辐射，因此这也是一种旋近态。不过由于两者质量比例悬殊，这种旋近态的变化比一般的双星系统更为缓慢，从观测的角度来说，这意味着可以用长达数年的时间观测到同一种波形 。这种引力辐射可近似为从一个克尔黑洞附近的一个质点放射出的啁啾信号，而质点的轨道有可能是高度偏心的（偏心率接近1）。随着引力辐射系统动能不断减少，这使得轨道的偏心率逐渐降低，在旋近态的后期有可能降低到0.4左右，在这段时间内EMRI的辐射频率稳定在LISA的测量频域之内 。其波形包含了黑洞附近的时空几何信息，尤其有可能通过对黑洞质量和自旋的观测来验证黑洞无毛定理 。

EMRI的发生率与星系的构成方式关系不大，所以LISA在一年的时间内有能力观测到这类事件上百次 。距离最近的事件有可能在红移小于0.1之内 ，前提是理论研究能够对质点运动的轨道在数十个周期内做出较为精确的预测。但在理论上预测这种轨道并不那么容易，主要原因在于围绕克尔黑洞的高度偏心轨道有可能是混沌的，如果质点的运动轨迹远离黑洞的赤道平面轨道将变得非常复杂，有可能在整个视界内高速游荡。想要准确预测数十个周期内的轨道运动，需要定义好的初始条件以及多达14个用来区分不同运动且足够精确的参数 ，这就导致探测筛选这种信号需要一组数量非常庞大的波形模板，完全计算这些模板甚至超越了现有计算机的计算能力 ，这导致单纯的模式匹配算法很可能并不适用于此。至今最常见的EMRI波形的数值解法是由康乃尔大学的索尔·图科斯基（Saul Teukolsky）于1970年代创立的图科斯基方程 。

大爆炸

  基于暴胀理论的星系起源，星系起源于最初质量密度的微扰，而这些微扰形成了今天的引力随机背景辐射

引力波自诞生起在宇宙中的传播至今就几乎没有衰减或散射 ，从引力子的角度看，是因为引力子具有非常小的散射截面 . 。宇宙微波背景辐射揭示了大爆炸之后10 年的宇宙状况，对太初核合成的研究揭示了大爆炸之后几分钟内的宇宙状况，而引力波的诞生则可以追溯到大爆炸之后小于10 秒的时间范围之内。对这种引力 随机背景辐射 （ 英语 ： stochastic background ） 的观测是引力波天文学最重要的课题之一 。

与一般情形下的引力波用平均振幅描述不同，引力波的随机背景辐射通常用波场的能量密度描述，这种随机背景辐射可以来自任何天体（例如双白矮星等双星发出的迷惑噪声），也可以来自大爆炸。对于宇宙学中的场，一般要将这个场的能量密度归一化到宇宙的临界密度 。尽管现在还不确定引力波场的能量密度的具体数值，但在当代宇宙学的框架下，背景辐射的能量密度受到太初核合成、微波背景辐射以及脉冲星计时的约束：太高的能流密度会破坏太初核合成理论的成立，太高的能量涨落则与实际各向异性非常小的微波背景辐射不符，而对毫秒脉冲星计时的观测证实了引力波的背景辐射强度不足以高到使脉冲星信号间隔发生可观测变化的程度 。

在描述早期宇宙的暴胀模型中，引力子在普朗克时期内产生，并有可能按照引力场和其他场的自由度均分，这就形成了其温度相当于微波背景辐射的引力波的热背景辐射。其后宇宙进入暴胀时期，暴胀对最初质量密度的形成提供了足够大的微扰，这种机制使星系能够形成。而这些微扰则以引力场微扰的形式传播至整个宇宙形成了随机背景辐射。引力波形成的随机背景辐射被认为是各向同性、静态且无偏振的。而暴胀理论预言下的频谱是平坦的，即能量密度与频率无关 。宇宙背景探测者（COBE）通过对微波背景辐射的观测得到在频率为10 赫兹处的能量密度上限为3×10 。如果暴胀理论是正确的，这意味着对所有频率的背景辐射都具有相同的能量密度。这样低的能量密度导致现有的任何探测器都无法捕捉到暴胀的引力波信号。在不同于暴胀的其他模型下，例如宇宙弦（cosmic string） 的振动也会产生能量密度与频率无关的引力辐射，而宇宙弦预言下的能量密度达到了当前可观测的量级 。

对于这种信号LIGO在频率100赫兹的灵敏度为10 ，但通过对两个探测器（例如LHO和LLO，或者LIGO和VIRGO，GEO600等）符合测量得到的结果进行互相关计算可提高到10 ，因此互相关是搜寻此信号的重要手段 。而Advanced LIGO在这个频率上的灵敏度预计可达到10 ；LISA在频率1毫赫兹的灵敏度可达10 ，但在实际观测中能否达到这个数值取决于双白矮星等产生的背景噪声是否会将随机宇宙背景辐射淹没。除此之外，r模式的中子星、双中子星和黑洞以及某些超新星爆发都有可能将频率高于0.1毫赫兹的宇宙背景辐射淹没 。一般认为来自双星的背景噪声在低于10微赫兹的频率下快速降低，因此微赫兹量级的空间探测器可能是探测宇宙随机背景辐射的最佳手段。

探测

引力波天文学

引力波天文学自20世纪中叶以来逐渐兴起，与传统的电磁波天文学不同的是，它通过测量引力波来研究各类相对论性天体及宇宙现象。引力相互作用对于电磁相互作用来说极为微弱，所以它的直接观测对现有技术而言还是一个很大的挑战。1916年阿尔伯特·爱因斯坦发表广义相对论，在理论上预言了引力波的存在，但之后百年中都未被直接观测到。然而通过各种间接手段，科学家已经为引力波的实际存在定下了强大的理论和实验基础。最著名的例子是普林斯顿大学的拉塞尔·赫尔斯和约瑟夫·泰勒所发现的赫尔斯－泰勒脉冲双星（PSR 1913+16）。这一系统的相互旋近现象是引力辐射能够使系统能量衰减的最佳证据，而两人也因此获得了1993年的诺贝尔物理学奖 。2014年3月17日，哈佛－史密松天体物理中心的天文学家宣布利用BICEP2探测器在宇宙微波背景中观测到B模偏振 ，但在后来的分析验证中发现无法排除星际尘埃的可能 ，该研究团队并于2015年1月30日承认资料判读有误 。若后续实验（例如BICEP3）能确切得到引力波效应的成果，将成为宇宙暴胀和大爆炸理论的强烈证据 。2016年2月11日，爱因斯坦预言引力波百年之际，激光干涉引力波天文台（LIGO）团队在华盛顿宣布于2015年9月14日9时51分许完成人类对于引力波的首次直接探测 。

引力波和电磁波所携带的有关波源的信息非常不同。引力波与波源整体的宏观运动直接相关，而非像电磁波一样来自于单个原子或电子的运动之叠加。例如对于一个双星系统，对引力波偏振的测量可以让科学家得知其轨道倾斜度，而这类有关波源运动的宏观信息是无法从电磁辐射观测中取得的。引力波波长一般是波源尺寸的几个数量级以内，而不像电磁波一样波长比波源尺寸小很多。这使得引力波天文学通常不能像电磁波天文学那样对波源进行拍照成相，而是类似声波直接从波形分析波源的性质。许多引力波源很难或根本无法通过电磁辐射直接观测到（例如黑洞），反之亦然。由于暗物质占星系物质的绝大部分，而且不发出任何电磁波 ，所以引力波天文学对这些暗物质的观测和研究具有重要意义。引力波的另一特点在于它几乎不与物质进行相互作用。来自远方天体甚至是宇宙诞生时所产生的引力波至今几乎没有发生衰减或散射，这意味着引力波可以作为研究宇宙深处的重要工具。宇宙形成后38万年，电磁波才开始能够穿透宇宙的物质 ，因此在这一堵“墙”以前的宇宙是无法通过电磁波来直接观测的，引力波也就成为了直接观测大爆炸的仅有工具 。

引力波探测器

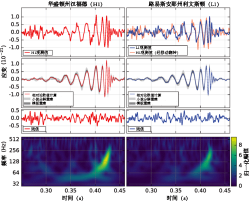
  LIGO位于汉福德（H1）及利文斯顿（L1）的两架干涉仪于2015年9月14日探测到的引力波事件GW150914。这是人类史上首个引力波直接探测结果。

剧烈事件所发出的引力波经过天文距离，在到达地球后，强度已降至很低的水平，振幅的数量级在10 以下 。再加上各种来自仪器内外的噪声，实际引力波信号的探测变得非常困难。因此在探测引力波时，仪器须有极高的精确度和降噪能力 。

第一架实际投入应用的引力波探测器是1960年代美国马里兰大学的约瑟夫·韦伯（Joseph Weber）制造的铝质实心圆柱 ，通常称为共振质量探测器或棒状探测器。各国科学家利用该探测器，并没有取得能令人信服的引力波信号证据 。

1970年代后，同样来自韦伯的激光干涉引力波探测器开始兴起。随着激光和镜面工艺的进步，这种新型的大型引力波探测器在世界各地甚至计划在空间建造起来，包括：激光干涉引力波天文台（LIGO） 、GEO600 、TAMA300 、VIRGO 以及还有美国和欧洲合作计划中的激光干涉空间天线（LISA） 等等。截至2012年 ( 2012-Missing required parameter 1= month ! ) ，最为敏感的探测器位于LIGO和VIRGO天文台，灵敏度高达 5 × 10 分之一 。

迈克耳孙干涉仪应用激光光束来测量两条相垂直的干涉臂的长度差变化 ，可以说是最直接的引力波探测器。最大的激光干涉引力波天文台LIGO主要由加州理工学院和麻省理工学院负责运行，也是美国国家科学基金会资助的最大科研项目之一 。其精确度数量级已经达到10 。VIRGO位于意大利比萨附近，是一架双臂长度为3千米的地面激光干涉探测器，自2007年起开始进行科学观测，并具有和LIGO相媲美的灵敏度。GEO600位于德国汉诺威，双臂长度为600米，其工作带宽为50赫兹至1.5千赫兹。一个称为Einstein@Home（爱因斯坦在你家）的分布式计算计划使公众能在个人电脑上通过此软件帮助分析LIGO和GEO600所采集的脉冲星数据 。

为了避免地球上众多的噪声来源，可通过人造卫星和航天器以高精度测量引力波。例如，科学家通过监测行星际航天器（如围绕木星和土星的航天器）的通信信号返回时间来观测引力波的特征影响 。欧洲空间局正在研究中的LISA项目将由三个相同的航天器组成一个边长为500万公里的等边三角形，整体沿地球轨道绕太阳公转。这个系统会监测引力波通过任意一个组成卫星时所造成的激光干涉上的变化 。

许多脉冲星可以作为极为精确的时钟。低频引力波通过地球时会造成时空扰动，使地球上的时钟和脉冲星的计时之间产生偏差。科学家由此已经推导出一些有关随机背景引力波的信息 。

直接探测

2016年2月11日，爱因斯坦提出广义相对论并预言引力波的存在100周年之际，LIGO团队在华盛顿特区召开新闻发布会，宣布LIGO在经过五年的系统升级之后完成人类历史上首个引力波直接探测结果，GW150914。这束引力波的信号于2015年9月14日9时51分（UTC）许被位于利文斯顿和汉福德的两架LIGO激光干涉仪几乎同时捕捉到 。根据探测信号，这束引力波来自位于南天的距地球约13亿光年的双黑洞。两个黑洞的质量分别约为太阳质量的29和36倍。它们经过互相旋近后融合为质量约为太阳62倍的黑洞，有约3倍太阳质量的能量在不到1秒的时间内以引力波的形式释出，其峰值功率达到了全宇宙的所有可见光功率的50倍。这次融合发生在约6亿至18亿年前。他们的探测结果的显著性大于5.1σ 。

进阶理论

阅读本节需要了解电动力学和广义相对论的基本概念，可直接参阅有关书籍 。

线因斯坦方程

  引力波——时空的波纹（示意图）

广义相对论预言下的引力波是以波形式传播的时空扰动，被形象地称为“时空涟漪” 。广义相对论下的弱引力场可写作对平直时空的线性微扰：（以下采用自然单位，引力常数 G 和光速 c 都设为1）

这里 η η --> α α --> β β --> = diag ( − − --> 1 , 1 , 1 , 1 ) {\displaystyle \eta _{\alpha \beta }={\text{diag}}(-1,1,1,1)} 是平直时空的闵可夫斯基度规， h α α --> β β --> {\displaystyle h_{\alpha \beta }} 是弱引力黎曼来的微扰。在这个度规下计算得到的黎曼张量为

爱因斯坦张量为

这里 h ¯ ¯ --> α α --> β β --> = h α α --> β β --> − − --> 1 2 η η --> α α --> β β --> h {\displaystyle {\bar {h}}_{\alpha \beta }=h_{\alpha \beta }-{\frac {1}{2}}\eta _{\alpha \beta }h} ， h = η η --> α α --> β β --> h α α --> β β --> {\displaystyle h=\eta ^{\alpha \beta }h_{\alpha \beta }} ， h ¯ ¯ --> α α --> β β --> {\displaystyle {\bar {h}}_{\alpha \beta }} 被称作迹反转度规微扰（ trace-reverse metric perturbation ）。

如果采用洛伦茨规范，爱因斯坦张量的后三项将为零，这里洛伦茨规范的形式为

事实上总可以选择这样的规范条件，并且洛伦茨规范不是唯一的，意味着坐标在一个无穷小的线性坐标变换下仍满足洛伦茨规范，关于这一点请参考有关规范变换的内容。

在洛伦茨规范下，爱因斯坦张量为

代入爱因斯坦引力场方程 G α α --> β β --> = 8 π π --> T α α --> β β --> {\displaystyle G_{\alpha \beta }=8\pi T_{\alpha \beta }} ，

这个方程又叫弱引力场中的线因斯坦方程。在远源（ T α α --> β β --> = 0 {\displaystyle T_{\alpha \beta }=0} ）的情形下，得到带有达朗贝尔算符的四维波方程：

引力波的传播

上面波方程的一般解为如下本征函数的线性叠加：

其中 A α α --> β β --> {\displaystyle A_{\alpha \beta }} 是四维振幅， k {\displaystyle \mathbf {k} 波矢 是四维波矢，满足条件

四维波矢 k α α --> = ( ω ω --> k → → --> , k → → --> ) {\displaystyle k^{\alpha }=\left(\omega _{\vec {k}},{\vec {k}}\right)} ，其中 ω ω --> k → → --> {\displaystyle \omega _{\vec {k}}} 是波的角频率， k → → --> {\displaystyle {\vec {k}}} 是经典的三维波矢。由于洛伦茨规范并不唯一，此时坐标还不是完全确定的。如果再加上条件：

第一个条件表示引力波张量中所有与时间 t 有关的分量都为零，第二个条件表示引力波张量矩阵的迹为零。因此这组规范条件叫做横向无迹规范（ transverse traceless gauge ），简称TT规范。在TT规范下， h ¯ ¯ --> α α --> β β --> = h α α --> β β --> {\displaystyle {\bar {h}}_{\alpha \beta }=h_{\alpha \beta }} 。 由洛伦茨规范和TT规范共同决定下的引力波张量只有两个分量是独立的，它们实际对应着引力波的两种偏振态。对于在z方向传播的波矢 k α α --> = ( ω ω --> , 0 , 0 , ω ω --> ) {\displaystyle k^{\alpha }=\left(\omega ,0,0,\omega \right)} ，这两个振动分量垂直于传播方向，这表明引力波和电磁波一样是横波，其张量形式写作

其中 h + {\displaystyle h_{+}} 和 h × × --> {\displaystyle h_{\times }} 分别为引力波的“十字型”和“交叉型”两种偏振态，上文引力波通过时的效应一段的两幅动画示意了两种偏振各自不同的振动形式。

引力波的辐射

有源的线因斯坦方程解释了波源的运动如何产生引力辐射：

类似用泊松方程求解牛顿引力势，运用格林函数可得到带有推迟势的一般解：

这里 T α α --> β β --> {\displaystyle T^{\alpha \beta }} 所处在的时间是 t − − --> | x → → --> − − --> x → → --> ′ ′ --> | {\displaystyle t-|{\vec {x}}-{\vec {x}}^{\prime }|} ，表示引力波从源点 x → → --> ′ ′ --> {\displaystyle {\vec {x}}^{\prime }} 传播到场点 x → → --> {\displaystyle {\vec {x}}} 经过了时间为 | x → → --> − − --> x → → --> ′ ′ --> | {\displaystyle |{\vec {x}}-{\vec {x}}^{\prime }|} 的延迟。

在远场近似和长波极限下，格林函数解近似为

其中标量 r = | x → → --> − − --> x → → --> ′ ′ --> | ≈ ≈ --> | x → → --> | {\displaystyle r=|{\vec {x}}-{\vec {x}}^{\prime }|\approx |{\vec {x}}|} 是源点到场点的距离。

相对论中波源的质能守恒和动量守恒合起来写作

因此动量-能量张量 T α α --> β β --> {\displaystyle T^{\alpha \beta }} 中的 T t t {\displaystyle T^{tt}} （质量-能量密度）和其他所有和时间t有关的分量 T i t {\displaystyle T^{it}} （动量密度）对时间的偏导数都为零，代入后方程的解可进一步化简为

这即是引力辐射的 四极矩近似公式 （ 英语 ： Quadrupole formula ） ，描述了一个弱相对论系统引力辐射的最基本情形。其中 Q α α --> β β --> {\displaystyle Q^{\alpha \beta }} 描述了波源的质量-能量分布

这里张量 Q α α --> β β --> {\displaystyle Q^{\alpha \beta }} 即是系统的质量四极矩（转动惯量张量），而 ρ ρ --> ≡ ≡ --> T t t {\displaystyle \rho \equiv T^{tt}} 是波源的质量-能量密度，积分范围是整个波源内部。

四极矩公式的物理意义是引力辐射起始于随时间二阶变化（例如谐振）的四极矩，这一点与电磁辐射不同：电磁辐射起始于随时间二阶变化的偶极矩。这一区别的来源是：一个随时间二阶变化的电偶极矩或磁偶极矩对应着电荷密度中心的振动，这一振动是随意不受限制的；而一个随时间二阶变化的质量的偶极矩对应着质心的振动，这一振动不能满足动量守恒定律，因此不存在这样对时间二阶偏导不为零的质量偶极矩。由于四极矩是偶极矩的更高阶项，这也是引力辐射要远弱于电磁辐射的原因。

引力波的能量

四极矩近似下引力波的光度（总辐射功率）为

这里 Q 是张量矩阵 Q i j {\displaystyle Q_{ij}} 的迹。 引力波的能量通量（单位面积的辐射功率）近似为

这里 f 是单色引力波的频率。

思考一个地面探测器可以感测到的微弱辐射暴，其频率为1000赫兹，到达地球时的引力强度为10 的引力波，则其能量通量约为 3 × × --> 10 − − --> 3 W / m 2 {\displaystyle 3\times 10^{-3}W/m^{2}} ，这相当于满月时地球从月球接收到的电磁辐射能量通量的两倍，大约有1ms之久，这引力波源是夜间天空最亮的星体。这表明引力波实际可以携带很大的能量，但与物质相互作用力非常小，这才是引力波难以被探测的根本原因。

参见

广义相对论

引力场

引力波天文学

霍金辐射

轨道共振

稳态理论

潮汐力

注释

^ 假设有两个距离为 L 的自由落体，引力波的振幅定义为两者间的距离变化占原距离的比例∆ L / L 。振幅与波源四极矩的二阶时间导数成正比 。

^ 啁啾质量定义为 M c h i r p = μ μ --> 3 / 5 M 2 / 5 {\displaystyle M_{chirp}=\mu ^{3/5}M^{2/5}} ， 其中 µ 是系统的折合质量，而 M 则是总质量。

^ 由此定义 Ω Ω --> G W ≡ ≡ --> 1 ρ ρ --> c d ρ ρ --> G W ( f ) d ln ⁡ ⁡ --> f {\displaystyle \Omega _{GW}\equiv {\frac {1}{\rho _{c}}}{\frac {d\rho _{GW}(f)}{d\ln f}}} 这个量描述了随机引力波的能量密度按频率分布情况，则引力背景辐射的总能流密度由对 Ω Ω --> G W {\displaystyle \Omega _{GW}} 从频率0至正无穷的积分给出。 ρ ρ --> c = 3 H 2 / 8 π π --> G {\displaystyle \rh弗里德曼方程=3H^{2}/8\pi G} 是弗里德曼方程下得到的宇宙临界密度值； H 是哈勃常数，如果以千米/秒·兆秒差距为单位，现在一般认为这个值在50到65之间 。

^ 因位置差异导致的到达时间不同，利文斯顿的干涉仪领先了7毫秒。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。