历史

球被压在弹性材料的过程中，接触面积逐渐增大。

经典接触力学主要跟海因里希·赫兹 。1882年赫兹解决了两个曲面弹性体的接触问题（也叫赫兹接触应力）。这种相关的典型的解决方法为现代接触力学奠定了基础。

直到近100年后，约翰逊，肯德尔和罗伯茨才找到一种近似的方法解决粘着接触问题 。

20世纪中期接触力学领域的进步要归功于Bowden和Tabor。Bowden和Tabor首次强调了接触中物体表面粗糙度的重要性。通过对表面粗糙度的研究发现，互相摩擦体间的真实接触面积要小于表面接触面积。这种解释也彻底改变了摩擦学的研究方向。Bowden和Tabor的著作产生了几种粗糙表面的接触力学理论。

在此领域中说到先驱著作，就必须提及1957年Archard的贡献 。Archard认为，即使是粗糙的弹性表面间，其接触面积与法向力接近比例关系。Greenwood与Williamson 、Bush 和Persson 分别于1966年、1975年和2002年在此方向上提出了更重要的认识。这些研究的主要发现如下：粗糙材料的接触面积通常与法向作用力成正比，而单个微观接触参数（如压力，微观接触尺寸）却很少取决于载荷。

无粘着弹性接触的经典问题

对于有简单几何外形的弹性体接触，其接触理论主要是计算接触面积和压入深度。常用的接触求解如下。

球体和弹性半空间体的接触

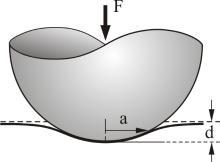
球体和弹性半空间的接触

一个半径为 R {\displaystyle R} 的球体在一个弹性半空间上压出的凹痕深度为 d {\displaystyle d} ，若产生的接触区域的半径为 a = R d {\displaystyle a={\sqrt {Rd}}} ，则作用力 F {\displaystyle F} 为 F = 4 3 E ∗ ∗ --> R 1 / 2 d 3 / 2 {\displaystyle F={\frac {4}{3}}E^{*}R^{1/2}d^{3/2}} ,

式中

1 E ∗ ∗ --> = 1 − − --> ν ν --> 1 2 E 1 + 1 − − --> ν ν --> 2 2 E 2 {\displaystyle {\frac {1}{E^{*}}}={\frac {1-\nu _{1}^{2}}{E_{1}}}+{\frac {1-\nu _{2}^{2}}{E_{2}}}} .

E 1 {\displaystyle E_{1}} , E 2 {\displaystyle E_{2}} 分别为是接触体的弹性模量， ν ν --> 1 {\displaystyle \nu _{1}} , ν ν --> 2 {\displaystyle \nu _{2}} 是泊松比。

两个球体的接触

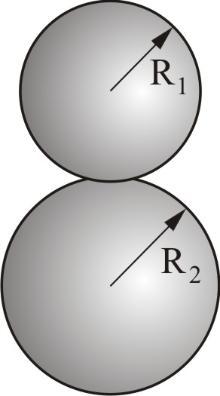
两个球体的接触

若给定两个球体的半径为 R 1 {\displaystyle R_{1}} 和 R 2 {\displaystyle R_{2}} , 定义 R {\displaystyle R} 为

1 R = 1 R 1 + 1 R 2 {\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}} ,

则接触区域的压力分布为

p = p 0 ( 1 − − --> r 2 a 2 ) 1 / 2 {\displaystyle p=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{1/2}} , 式中

p 0 = 2 π π --> E ∗ ∗ --> ( d R ) 1 / 2 {\displaystyle p_{0}={\frac {2}{\pi }}E^{*}\left({\frac {d}{R}}\right)^{1/2}} .

对于 ν ν --> = 0.33 {\displaystyle \nu =0.33} ，最大剪应力发生在表面下 z ≈ ≈ --> 0.49 a {\displaystyle z\approx 0.49a} 位置。

两个等半径圆柱体的交叉接触

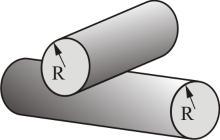
两个相同半径的交叉圆柱体的接触

该接触等同于一个半径为 R {\displaystyle R} 的球体和一个平面的接触（见上）。

刚性圆柱体和弹性半空间体的接触

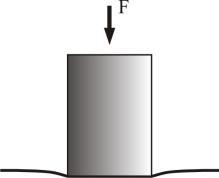
刚性圆柱体和弹性半空间的接触

一个刚性圆柱体压在一个弹性半空间上，产生的压力分布可写为

p = p 0 ( 1 − − --> r 2 a 2 ) − − --> 1 / 2 {\displaystyle p=p_{0}\left(1-{\frac {r^{2}}{a^{2}}}\right)^{-1/2}} , 式中

p 0 = 1 π π --> E ∗ ∗ --> d a {\displaystyle p_{0}={\frac {1}{\pi }}E^{*}{\frac {d}{a}}} .

凹痕的深度和法向力的关系可表述为

F = 2 a E ∗ ∗ --> d {\displaystyle F=2aE^{*}d{\frac {}{}}} .

刚性圆锥体和弹性半空间体的接触

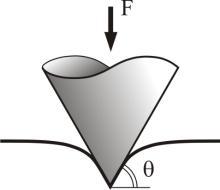
刚性圆锥体和弹性半空间的接触

一个刚性圆锥体和一个弹性半空间作用时，压痕的深度和接触半径的关系为

d = π π --> 2 a tan ⁡ ⁡ --> θ θ --> {\displaystyle d={\frac {\pi }{2}}a\tan \theta } ,

式中 θ θ --> {\displaystyle \theta } 为圆锥侧面和平面的夹角，则压力分布为

p ( r ) = − − --> E d π π --> a ( 1 − − --> ν ν --> 2 ) l n ( a r + ( a r ) 2 − − --> 1 ) {\displaystyle p(r)=-{\frac {Ed}{\pi a\left(1-\nu ^{2}\right)}}ln\left({\frac {a}{r}}+{\sqrt {\left({\frac {a}{r}}\right)^{2}-1}}\right)} .

在圆锥顶尖应力有个对数奇点。总作用力为

F N = 2 π π --> E d 2 tan ⁡ ⁡ --> θ θ --> {\displaystyle F_{N}={\frac {2}{\pi }}E{\frac {d^{2}}{\tan \theta }}} .

两个中心轴平行的圆柱体间的接触

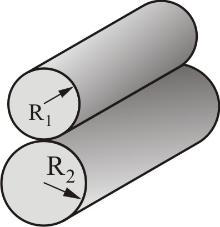
两个中心轴平行的圆柱体间的接触

两个中心轴平行的圆柱体接触时，作用力与压痕深度成线性比例关系：

F = π π --> 4 E ∗ ∗ --> L d {\displaystyle F={\frac {\pi }{4}}E^{*}Ld} .

次关系式曲率半径完全没有关系。接触半径可用通常的关系式来描述：

a = R d {\displaystyle a={\sqrt {Rd}}} ,

与两个球体的接触一样，式中

1 R = 1 R 1 + 1 R 2 {\displaystyle {\frac {1}{R}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}} ,

最大压力为

p 0 = ( E ∗ ∗ --> F π π --> L R ) 1 / 2 {\displaystyle p_{0}=\left({\frac {E^{*}F}{\pi LR}}\right)^{1/2}} .

降维法

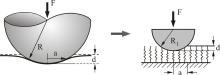
球体和弹性半空间体的接触以及其一维替代模型

很多接触问题都可以采用降维法来简单地解决。 降维法中，三维接触问题可以用一个物体和一个线弹性或线粘弹性基体的接触来替代（见图）。如果根据降维法的法则来修改该物体的形状并定义该弹性或粘弹性基体，则一维系统与原来的三维系统的性质完全一样 。

无粘着赫兹理论

经典接触理论主要是无粘着接触，也就是在接触面内没有张力，接触双方分开时没有粘着力。目前分析方法和数值方法已经被用于解决这类问题。当两个物体接触时，存在复杂的力和单元的传递，因此该接触问题变得很复杂。另外，接触应力和应变关系通常是非线性的。为了简化问题，通常参考系的定义使得处于其中的物体是静态的（物体之间也可能有相对运动）。物体在接触界面通过表面牵引力（或表面应力）相互影响。The 考虑两个物体接触，接触表面在( x {\displaystyle x} , y {\displaystyle y} )-平面的方程为 S {\displaystyle S} ， z {\displaystyle z} -轴垂直于表面。其中一个物体在 S {\displaystyle S} 内将经历一个法向压力分布 p z = p ( x , y ) = q z ( x , y ) {\displaystyle p_{z}=p(x,y)=q_{z}(x,y)} 和平面上表面牵引力分布 q x = q x ( x , y ) {\displaystyle q_{x}=q_{x}(x,y)} 和 q y = q y ( x , y ) {\displaystyle q_{y}=q_{y}(x,y)} 。根据牛顿力平衡，得到下面这几个力必须平衡，并与另外一个物体受的力相反：

这些力产生的力矩也要相互抵消，从而保证其运动稳定性：

赫兹理论中的假设

应变很小并在弹性范围内；

接触物体可以看作是弹性半空间体，也就是说，接触面远小于物体半径；

表面是连续的，不确定的 ；

表面无摩擦。

不满足这些条件的接触问题更加复杂，通常称之为 非赫兹 接触。

解析解的求解方法

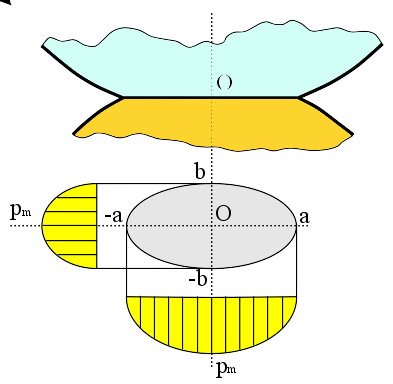
两个球体的接触。

无粘着接触的理论解可以按照接触面的几何形状分为两种。一种是确定性接触，变形发生前两个物体有多点接触。另一种是非确定性接触，两个接触物体的形状完全不同，以至于在零载荷下，它们只有一个点或一条线接触。在非确定性接触中，接触面积跟物体的尺寸相比，要小很多，而且该接触面的应力非常大。 对于线弹性材料接触，通常采用的方法是叠加，将不同接触点的解直接相加。比如半空间体的加载问题，通常将Flamant解作为起始点，然后产生不同形状的接触面。两个物体间的力平衡和力矩平衡作为附加约束再来求解。

粗糙表面间的接触

当两个粗糙表面相互挤压时，真实的接触面积 A {\displaystyle A} 远小于表观接触面积 A 0 {\displaystyle A_{0}} 。在一个“任意粗糙”的表面和一个弹性半球体接触时，真实的接触面积与法向作用力 F {\displaystyle F} 的关系为

A = κ κ --> E ∗ ∗ --> h ′ F {\displaystyle A={\frac {\kappa }{E^{*}h"}}F} ,

式中 h ′ {\displaystyle h"} 等于表面斜度的均方根（也叫均方值），且 κ κ --> ≈ ≈ --> 2 {\displaystyle \kappa \approx 2} 。真实接触面积的平均压力为

σ σ --> = F A ≈ ≈ --> 1 2 E ∗ ∗ --> h ′ {\displaystyle \sigma ={\frac {F}{A}}\approx {\frac {1}{2}}E^{*}h"}

该压力可适当估算为有效弹性模量与表面斜度 h ′ {\displaystyle h"} 均方值的乘积的一半。

若给定压力远大于材料的硬度 σ σ --> 0 {\displaystyle \sigma _{0}} 时，下式

Ψ Ψ --> = E ∗ ∗ --> h ′ σ σ --> 0 > 2 {\displaystyle \Psi ={\frac {E^{*}h"}{\sigma _{0}}}>2}

描述了完全塑性状态下的微观粗糙度。当 Ψ Ψ --> 2 3 {\displaystyle \Psi 时，表面为弹性接触。参数 Ψ Ψ --> {\displaystyle \Psi } 由Greenwoord和Williamson引入作为塑性指数. 无论系统表现为塑性还是弹性，均与法向作用力为无关。

参考文献

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。