历史

基于随机抽样的蒙特卡洛方法可以追溯到20世纪40年代。布鲁斯·艾布拉姆森（Bruce Abramson）在他1987年的博士论文中探索了这一想法，称它“展示出了准确、精密、易估、有效可计算以及域独立的特性“。他深入试验了井字棋，然后试验了黑白棋和国际象棋的机器生成的评估函数。1992年，B·布鲁格曼（B. Brügmann）首次将其应用于对弈程序，但他的想法未获得重视。2006年堪称围棋领域蒙特卡洛革命的一年，雷米·库洛姆（Remi Coulom）描述了蒙特卡洛方法在游戏树搜索的应用并命名为蒙特卡洛树搜索。列文特·科奇什（Levente Kocsis）和乔鲍·塞派什瓦里（Csaba Szepesvári）开发了UCT算法，西尔万·热利（Sylvain Gelly）等人在他们的程序MoGo中实现了UCT。2008年，MoGo在九路围棋中达到段位水平，Fuego程序开始在九路围棋中战胜实力强劲的业余棋手。2012年1月，Zen程序在19路围棋上以3：1击败二段棋手约翰·特朗普（John Tromp）。

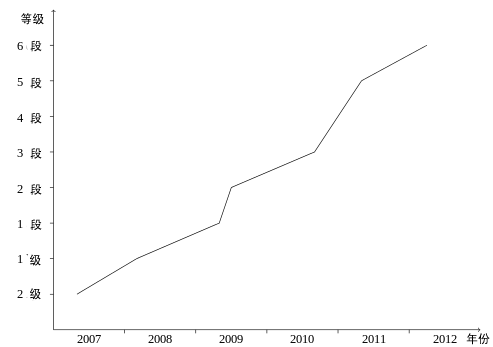
自2007年以来KGS围棋服务器上最优秀围棋程序的评级。自2006年以来，最优秀的程序全部使用蒙特卡洛树搜索。

蒙特卡洛树搜索也被用于其他棋盘游戏程序，如六贯棋、三宝棋、亚马逊棋和印度斗兽棋；即时电子游戏，如《吃豆小姐（英语：Ms. Pac-Man）》、《神鬼寓言:传奇（英语：Fable Legends）》、《罗马II：全面战争》；不确定，如斯卡特、扑克、万智牌、卡坦岛。

原理

蒙特卡洛树搜索的每个循环包括四个步骤：

选择（Selection）：从根结点R开始，选择连续的子结点向下至叶子结点L。下面的结点有更多选择子结点的方法，使游戏树向最优点扩展移动，这是蒙特卡洛树搜索的本质。

扩展（Expansion）：除非任意一方的输赢导致游戏结丛，否则L会创建一个或多个子结点或从结点C中选择。

仿真（Simulation）：在结点C中进行随机布局。

反向传播（Backpropagation）：使用布局结果更新从C到R的路径上的结点信息。

每一个节点的内容代表胜利次数/游戏次数

蒙特卡洛树搜索的步骤

探索与利用

选择子结点的主要困难是在较高平均胜率的移动后对深层次变型的利用和对少数模拟移动的探索二者中保持某种平衡。第一个在游戏中平衡利用与探索的公式被称为UCT（Upper Confidence Bound 1 applied to trees，上限置信区间算法 ），由匈牙利国家科学院计算机与自动化研究所高级研究员列文特·科奇什与阿尔伯塔大学全职教授乔鲍·塞派什瓦里提出。UCT基于奥尔（Auer）、西萨-比安奇（Cesa-Bianchi）和费舍尔（Fischer）提出的UCB1公式，并首次由马库斯等人应用于多级决策模型（具体为马尔可夫决策过程）。科奇什和塞派什瓦里建议选择游戏树中的每个结点移动，从而使表达式 wini+cln⁡ ⁡ -->tni{\displaystyle {\frac {w_{i}}{n_{i}}}+c{\sqrt {\frac {\ln t}{n_{i}}}}}具有最大值。在该式中：

wi代表第i次移动后取胜的次数；

ni代表第i次移动后仿真的次数；

c为探索参数—理论上等于√2；在实际中通常可凭经验选择；

t代表仿真总次数，等于所有ni的和。

大多数当代蒙特卡洛树搜索的实现都是基于UCT的一些变形。

参见

AlphaGo，一个同时使用蒙特卡洛树搜索和深度学习的相当于人类的围棋程序。

延伸阅读

Cameron Browne, Edward Powley, Daniel Whitehouse, Simon Lucas, Peter I. Cowling, Philipp Rohlfshagen, Stephen Tavener, Diego Perez, Spyridon Samothrakis, Simon Colton.A Survey of Monte Carlo Tree Search Methods（蒙特卡洛树搜索方法综述）(PDF). IEEE Transactions on Computational Intelligence and AI in Games. March 2012, 4 (1). 

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。