发现过程及地位

库仑扭秤（ torsion balance ）示意图。库仑使用扭秤来测量两个点电荷彼此互相作用的静电力，因此发现库仑定律。

1767年，英格兰化学家约瑟夫·普利斯特里猜测电荷之间的相互作用力具有类似于万有引力的平方反比形式。

1769年，苏格兰物理学家约翰·罗比逊首次通过实验发现两个带电球体之间的作用力与它们之间距离的2.06次方成反比。

1770年代早期，著名英国物理学家亨利·卡文迪什通过巧妙的实验，得出了带电体之间的作用力依赖于带电量与距离，并得出静电力与距离的 2 ± ± --> 1 50 {\displaystyle 2\pm {\frac {1}{50}}} 次方成反比，只是卡文迪什没有公布这个结果。

后来，麦克斯韦利用与卡文迪什类似的方法，得出静电力与距离的 2 ± ± --> 1 21600 {\displaystyle 2\pm {\frac {1}{21600}}} 次方成反比的结果。

库仑定律是电学的基本定律，其中平方反比关系是否精确成立尤其重要，而根据现代量子场论，静电力的平方反比关系是与光子的静质量是否精确为零相关的，所以，对静电力的平方反比关系的精确验证，关系着现代物理学基本理论的基础。当前对库仑定律平方反比关系的验证越来越精确，如1971年进行的一次实验，给出库仑定律与平方反比关系的偏差小于 2.7 × × --> 10 − − --> 16 {\displaystyle 2.7\times 10^{-16}} 。

纯量形式

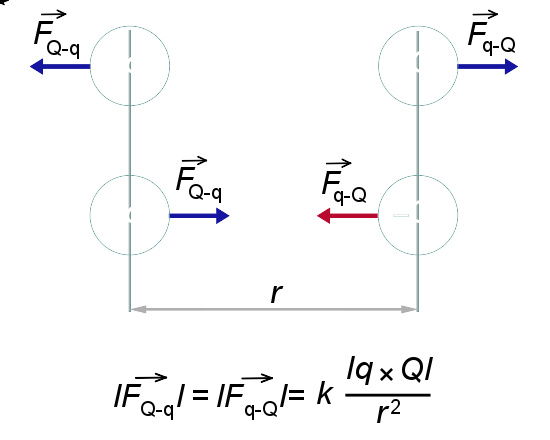
该图描述了库仑定律的基本原理：同号电荷相互排斥，异号电荷相互吸引。

库仑定律的标量形式只描述两个点电荷彼此相互作用的静电力的大小。一个电量为 q ′ {\displaystyle q"} 的点电荷作用于另一个电量为 q {\displaystyle q} 的点电荷，其静电力 F {\displaystyle F} 的大小，可以用方程表达为

其中， r {\displaystyle r} 是两个点电荷之间的距离， k e {\displaystyle k_{\mathrm {e} }} 是 库仑常数 。

库仑常数与真空电容率的关系方程为

正值的 F {\displaystyle F} 表示排斥力；而负值则表示牵引力 。

采用国际单位制，真空电容率 ϵ ϵ --> 0 {\displaystyle \epsilon _{0}} 的值是 8.854 187 817 × × --> 10 − − --> 12 {\displaystyle 8.854\ 187\ 817\times 10^{-12}厘米-克-秒制采用厘米-克-秒制， 单位电荷 （ e静库仑 ），又称为静库仑（ statcoulomb ），定义为使库仑常数 k e {\displaystyle k_{\mathrm {e} }} 为1的数值。

库仑定律的标量公式表明，力量的大小直接地与两个点电荷的电量成正比，又与两个点电荷之间距离的平方成反比。根据实验数据，距离的指数，与 − − --> 2 {\displaystyle -2} 的偏差，低于十亿分之一 ！

矢量形式

给予两个电量分别为 q {\displaystyle q} 、 q ′ {\displaystyle q"} ，位置分别为 r {\displaystyle \mathbf {r} } 、 r ′ {\displaystyle \mathbf {r} "} 的点电荷。为了要得到点电荷 q ′ {\displaystyle q"} 作用于点电荷 q {\displaystyle q} 的力量 F {\displaystyle \mathbf {F} } 的大小与方向，必须使用库仑定律的矢量形式：

假若两个点电荷同性（电荷的正负号相同），则其电量的乘积 q q ′ {\displaystyle qq"} 是正值，两个点电荷互相排斥。反之，假若两个点电荷异性（电荷的正负号相反），则其电量的乘积 q q ′ {\displaystyle qq"} 是负值，两个点电荷互相吸引。

电场

根据洛伦兹力定律，

其中， F {\displaystyle \mathbf {F} } 是洛伦兹力， E {\displaystyle \mathbf {E} } 是电场， v {\displaystyle \mathbf {v} } 是电荷的运动速度， B {\displaystyle \mathbf {B} } 是磁场。

假设，电荷静止不动：

则 F = q E {\displaystyle \mathbf {F} =q\mathbf {E} } 。

所以，一个电量为 q ′ {\displaystyle q"} ，位置为 r ′ {\displaystyle \mathbf {r} "} 的点电荷，所产生的电场 E {\displaystyle \mathbf {E} } 在位置 r {\displaystyle \mathbf {r} } 为

假若电荷是正值，电场的方向是从点电荷以径向朝外指出；假若是负值，则电场的方向是反方向。电场的单位是V/m或N/C。

离散电荷系统

由 N {\displaystyle N} 个点电荷所组成的一个系统，其作用于一个电量为 q {\displaystyle q} ，位置为 r {\displaystyle \mathbf {r} } 的检验电荷的静电力，可以用叠加原理来计算：

其中， q i ′ {\displaystyle q_{i}"} 和 r i ′ {\displaystyle \mathbf {r} _{i}"} 分别是第 i {\displaystyle i} 个点电荷的电量和位置。

连续电荷分布

对于一个连续电荷分布，我们可以将每一个无穷小的空间元素视为一个电量为 d q {\displaystyle dq} 的点电荷，做无限求和。这程序等价于连续电荷分布的区域积分。

线电荷分布（例如，一根带电的直线）的电量为

其中， λ λ --> ( r ′ ′ --> ) {\displaystyle \lambda (\mathbf {r^{\prime }} )} 是位于 r ′ ′ --> {\displaystyle \mathbf {r^{\prime }} } 的线电荷密度（每单位长度所带的电量)， d l ′ ′ --> {\displaystyle dl^{\prime }} 是一个无穷小线元素。

表面电荷分布（例如，两平行金属板电容器的一片带电的金属板）的电量为

其中， σ σ --> ( r ′ ′ --> ) {\displaystyle \sigma (\mathbf {r^{\prime }} )} 是位于 r ′ ′ --> {\displaystyle \mathbf {r^{\prime }} } 的面电荷密度（每单位面积所带的电量)， d a ′ ′ --> {\displaystyle da^{\prime }} 是一个无穷小面积元素。

体积电荷分布（例如，一个带电的圆球）的电量为

其中， σ σ --> ( r ′ ′ --> ) {\displaystyle \sigma (\mathbf {r^{\prime }} )} 是位于 r ′ ′ --> {\displaystyle \mathbf {r^{\prime }} } 的体电荷密度（每单位体积所带的电量)， d τ τ --> ′ ′ --> {\displaystyle d\tau ^{\prime }} 是一个无穷小体积元素。

作用于一个电量为 q {\displaystyle q} 的检验电荷的静电力 F {\displaystyle \mathbf {F} } ，可以表达为

其中， r {\displaystyle \mathbf {r} } 是检验电荷的位置， d q ′ {\displaystyle dq"} 是位于 r ′ ′ --> {\displaystyle \mathbf {r} ^{\prime }} 的无穷小电荷元素。

静电近似

在上述两种表述里，只有当点电荷是处于固定状态的时候，库仑定律才是完全正确的；假若点电荷处于缓慢的运动状态，则只能说库仑定律是大概正确。这条件称为静电近似。当几个点电荷处于相对运动状态的时候，根据爱因斯坦的相对论，会有磁场产生，这连带地改变了作用于点电荷的力量。

物理量表格

参阅

镜像法

库仑

电磁学

电场

物理学定律列表

参考文献

Griffiths, David J. Introduction to Electrodynamics（3rd ed.）. Prentice Hall. 1998. ISBN 0-13-805326-X. * Tipler, Paul. Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics（5th ed.）. W. H. Freeman. 2004. ISBN 0-7167-0810-8.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。