秦九韶算法
历史

伟烈亚力《中国科学扎纪》论秦九韶玲珑开方
19世纪初,英国数学家威廉·乔治·霍纳重新发现并证明,后世称作 霍纳算法 或 Horner scheme ) 。但是,19世纪英国传教士伟烈亚力最早对霍纳的发明权提出质疑。他在1852年著的《中国科学扎记》(Jointings on the Sciencs of the Chinese)一篇论文中,详细介绍秦九韶的正负开方术之后写道“读者不难认出这就是霍纳在1819年因为发表《解所有次方程》论文,被数学家奥古斯都·德·摩根评为‘必使其发明人因发现此算法而置身于重要发明家之列’的方法;我以为应该对霍纳的发明权提出辩驳。欧洲的朋友们可能会觉得意外,一位来自天朝帝国的竞争者,有更大的机会确立他的优先权” 。 此后,日本数学史家三上义夫在《中日数学史》一书中在详述秦九韶的正负开方术后写道:“谁能否认,霍纳的辉煌方法,至少在早于欧洲六百年之前,已经在中国运用了。” 。三上义夫还最先指出,秦九韶算法起源于汉代《九章算术》的开方法。其后王玲和李约瑟有专文论述秦九韶算法起源于《九章算术》。前苏联数学史家尤什克维奇说“这是中国传统数学最伟大成就之一”,他还说印度人不知有此方法,而阿拉伯数学家可能从中国前人传入此方法 。
下面以自今到古的顺序,列出早在霍纳之前对该算法的发现:
1809年,保罗·鲁菲尼
1669年,艾萨克·牛顿(但缺乏详细引文)
14世纪,中国数学家朱世杰
13世纪,中国数学家秦九韶在《数书九章》中
12世纪,波斯的数学家Sharaf al-Dīn al-Tūsī
11世纪(宋朝),中国数学家贾宪
汉朝(公元前202到公元220年),刘徽所注的《九章算术》中
霍纳在1819年发表的《解所有次方程》论文中的算例,其算法程序和数字处理都远不及五百多年前的秦九韶有条理;秦九韶算法不仅在时间上早于霍纳,也比较成熟。
元代数学家李冶和朱世杰继承了秦九韶算法。
秦九韶程序

− − --> x 4 + 763200 x 2 − − --> 40642560000 = 0 {\displaystyle -x^{4}+763200x^{2}-40642560000=0}
秦九韶算法 精确解x=840
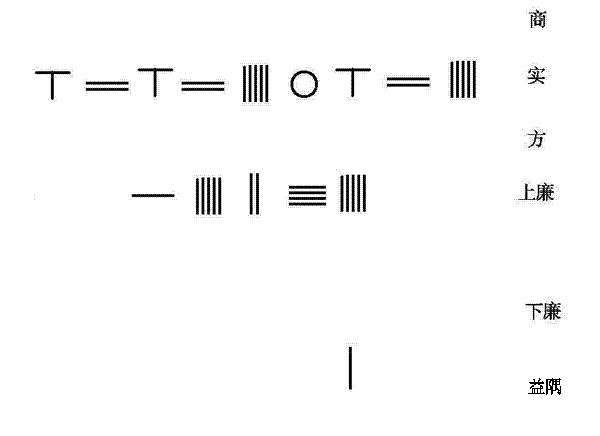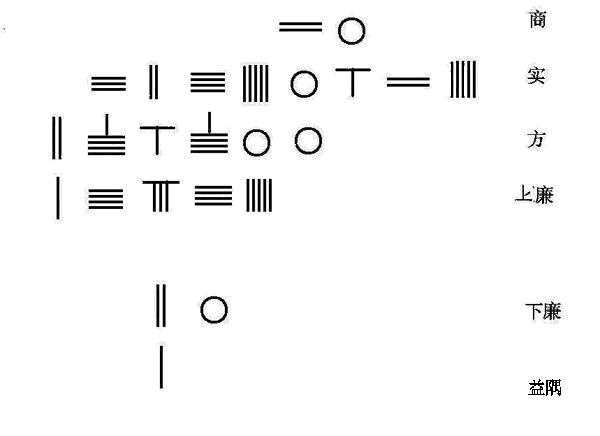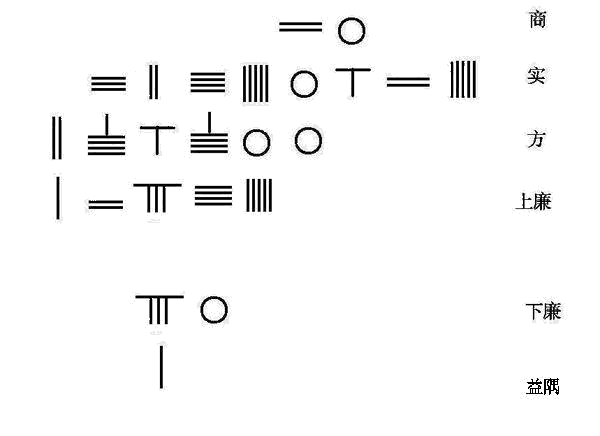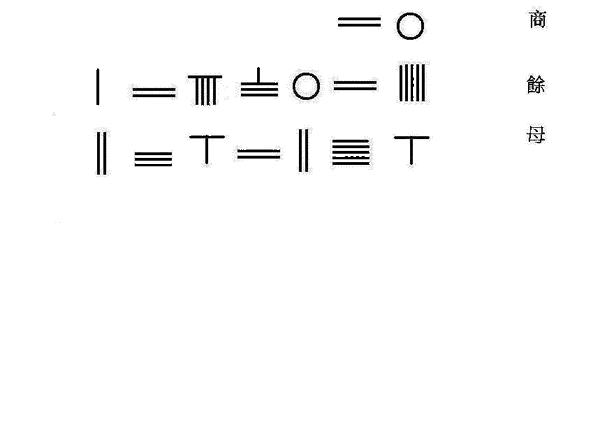
− − --> x 4 + 15245 x 2 − − --> 6262506.25 = 0 {\displaystyle -x^{4}+15245x^{2}-6262506.25=0} 秦九韶算法 近似解x=20.5
南宋数学家秦九韶将贾宪的增乘开方术推广,以求解任意高次方程的实数根的数值解。秦九韶的《数书九章》详细叙述用秦九韶算法求解二十六个二次到十次方程的的实数根的数值解,其中包含二十个二次方程,一个三次方程,四个四次方程和一个十次方程。 ;其中有些得到精确解;多数得近似解。
《数书九章》“《遥度圆城》”题列出一个十次方程,求解圆城的直径:
《数书九章》“《兴田求积》”题列出一个四次方程,
− − --> x 4 + 763200 x 2 − − --> 40642560000 = 0 {\displaystyle -x^{4}+763200x^{2}-40642560000=0}
设 a x 4 + b x 3 + c x 2 + d x + e = 0 {\displaystyle ax^{4}+bx^{3}+cx^{2}+dx+e=0}
其中 a=-1,b=0,c=763200,d=0,e=-40642560000
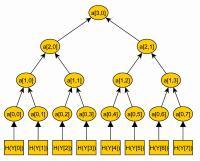
第一次估根~800;作y=x-800减根代换,估出根的第二位数字为y=40;经过第二次减根代换z=y-40后常数项抵消为0;得 精确解 y=40;x=800+y=800+40=840。右图为用阿拉伯数字表示的解此四次方程的秦九韶程序图(c"、d"、e"是运算过程中的临时数,最终分别并入c、d、e)。
《数书九章》“《环田三积》”题列出另一个四次方程,
其中经过x=10x"扩根代换和 x"=y+2减根代换得
− − --> 10000 y 4 − − --> 80000 y 3 + 1284500 y 2 + 577800 y − − --> 324506.25 = 0 {\displaystyle -10000y^{4}-80000y^{3}+1284500y^{2}+577800y-324506.25=0}
再次作扩根变换令z=10y 得:
− − --> z 4 − − --> 80 z 3 + 12845 x 2 + 57780 z − − --> 324506.25 = 0 {\displaystyle -z^{4}-80z^{3}+12845x^{2}+57780z-324506.25=0}
筹算程序:
置6262506.25为实
置15245为上廉
置1为益隅
上廉超二位,益隅超三位。
置商20步
以商乘益隅入下廉
以下廉乘商生负廉
以负廉与正廉相消得正上廉
以商乘上廉为方
以方乘商除实
又以商乘益隅入下廉
以下廉乘商生负廉
负廉与正廉相消
商与上廉生方
商隅相乘入下廉
商与下廉生负廉
负廉与正廉相消
商又与隅生下廉
下廉 三退 ,隅四退
无商(商第二位为0),以上廉并入方,并益隅入下廉
益隅并负廉与正方廉相消,命为母
约分
得x~ 20 1298025 2362256 {\displaystyle 20{\frac {1298025}{2362256}}} 其中: 1298025 2362256 {\displaystyle {\frac {1298025}{2362256}}} 不等于0,其第一位有效数字=0.5;即商的下一位数字为5,商~20.5,按秦九韶程序的一般规则,运算须继续进行下去直到“实”=0为止;但秦九韶在商=20.5而止,因20.5的精确度已满足在相关问题的需要。
三上义夫特别指出(1)秦九韶在处理 − − --> x 4 + 15245 x 2 − − --> 6262506.25 = 0 {\displaystyle -x^{4}+15245x^{2}-6262506.25=0} 这一类四次方程式时,绝非作为 x 2 {\displaystyle x^{2}} 的二次方程式来求解(所谓双二次方程),而是按四次方程来求解的。(2)秦九韶算法同样可以求出小数点后的数值,后来的中国数学家和日本数学正是这么做的。
原理
设有 n + 1 {\displaystyle n+1} 项的 n {\displaystyle n} 次函数
f ( x ) = a n x n + a n − − --> 1 x n − − --> 1 + a n − − --> 2 x n − − --> 2 + . . . . . . + a 2 x 2 + a 1 x + a 0 {\displaystyle f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+......+a_{2}x^{2}+a_{1}x+a_{0}}
将前 n {\displaystyle n} 项提取公因子 x {\displaystyle x} ,得
f ( x ) = ( a n x n − − --> 1 + a n − − --> 1 x n − − --> 2 + a n − − --> 2 x n − − --> 3 + . . . . . . + a 2 x + a 1 ) x + a 0 {\displaystyle f(x)=(a_{n}x^{n-1}+a_{n-1}x^{n-2}+a_{n-2}x^{n-3}+......+a_{2}x+a_{1})x+a_{0}}
再将括号内的前 n − − --> 1 {\displaystyle n-1} 项提取公因子 x {\displaystyle x} ,得
f ( x ) = ( ( a n x n − − --> 2 + a n − − --> 1 x n − − --> 3 + a n − − --> 2 x n − − --> 4 + . . . . . . + a 2 ) x + a 1 ) x + a 0 {\displaystyle f(x)=((a_{n}x^{n-2}+a_{n-1}x^{n-3}+a_{n-2}x^{n-4}+......+a_{2})x+a_{1})x+a_{0}}
如此反复提取公因子 x {\displaystyle x} ,最后将函数化为
f ( x ) = ( ( ( a n x + a n − − --> 1 ) x + a n − − --> 2 ) x + . . . . . . + a 1 ) x + a 0 {\displaystyle f(x)=(((a_{n}x+a_{n-1})x+a_{n-2})x+......+a_{1})x+a_{0}}
令
f 1 = a n x + a n − − --> 1 {\displaystyle f_{1}=a_{n}x+a_{n-1}}
f 2 = f 1 x + a n − − --> 2 {\displaystyle f_{2}=f_{1}x+a_{n-2}}
f 3 = f 2 x + a n − − --> 3 {\displaystyle f_{3}=f_{2}x+a_{n-3}}
......
f n = f n − − --> 1 x + a 0 {\displaystyle f_{n}=f_{n-1}x+a_{0}}
则 f n {\displaystyle f_{n}} 即为所求
应用示例
求当 x = 3 {\displaystyle x=3} 时 f ( x ) = 2 x 3 − − --> 6 x 2 + 2 x − − --> 1 {\displaystyle f(x)=2x^{3}-6x^{2}+2x-1\,} 的值。 反复提取公因子 x {\displaystyle x} 后,原函数可以写成 f 1 ( x ) = x ( x ( 2 x − − --> 6 ) + 2 ) − − --> 1 {\displaystyle f_{1}(x)=x(x(2x-6)+2)-1} 。建立下列 系速度 可以用来加快演算速度:
第四行中的数是表中本列上方两数之和。第三行的数字是x的值与左下方第四行数的乘积。第二行的数是多项式各项按照次数从大到小排列后的系数。表中右下角的数就是函数的值:5。
效率
对于一个n次的多项式函数,用常规方法(用重复乘法计算幂,再把各项相加)计算出结果最多需要n次加法和 ( n 2 + n ) 2 {\displaystyle {\frac {(n^{2}+n)}{2}}} 次乘法。若用x迭代的方法计算幂则需要n次加法和2n+1次乘法。如果计算中的数值数据是以字节方式储存的,那么常规方法约需要x占用的字节的2n倍空间。
而使用秦九韶算法时,至多只需作n次加法和n次乘法,最多需要x占用的字节的n倍空间。
意义
该算法看似简单,其最大的意义在于将求n次多项式的值转化为求n个一次多项式的值。在人工计算时,利用秦九韶算法和其中的系数表可以大幅简化运算;对于计算机程序算法而言,加法比乘法的计算效率要高很多,因此该算法仍有极大的意义,用于减少CPU运算时间。
参考文献
来源
李庆扬、王能超、易大义 (编). 《数值分析》 第四版. 清华大学出版社、Springer出版社. ISBN 7-302-04561-5.
参见
秦九韶
多项式方程求解
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值



24小时热门
推荐阅读

关于我们

APP下载





































