定义

  函数f的部分图像。每个实数的x都与f（x） = x − 9x相联系。

从输入值集合 X {\displaystyle X} 到可能的输出值集合 Y {\displaystyle Y} 的函数 f {\displaystyle f} （记作 f : X → → --> Y {\displaystyle f:X\to Y} ）是 X {\displaystyle X} 与 Y {\displaystyle Y关系的关系，满足如下条件：

f {\displaystyle f} 是完全的：对集合 X {\displaystyle X} 中任一元素 x {\displaystyle x} 都有集合 Y {\displaystyle Y} 中的元素 y {\displaystyle y} 满足 x f y {\displaystyle xfy} （ x {\displaystyle x} 与 y {\displaystyle y} 是 f {\displaystyle f} 相关的）。即，对每一个输入值， y {\displaystyle y} 中都有与之对应的输出值。

f {\displaystyle f} 是多对一的：若 f ( x ) = y {\displaystyle f(x)=y} 且 f ( x ) = z {\displaystyle f(x)=z} ，则 y = z {\displaystyle y=z} 。即，多个输入可以映射到一个输出，但一个输入不能映射到多个输出。

定义域中任一 x {\displaystyle x} 在到达域中唯一对应的 y {\displaystyle y} 记为 f ( x ) {\displaystyle f(x)} 。

比上面定义更简明的表述如下：从 X {\displaystyle X} 映射到 Y {\displaystyle Y} 的函数 f {\displaystyle f} 是 X {\displaystyle X} 与 Y {\displaystyle Y} 的直积 X × × --> Y {\displaystyle X\times Y子集的子集。 X {\displaystyle X} 中任一 x {\displaystyle x} 都与 Y {\displaystyle Y} 中的 y {\displaystyle y} 唯一对有序对有序对 ( x , y ) {\displaystyle (x,y)} 属于 f {\displaystyle f} 。

X {\displaystyle X} 与 Y {\displaystyle Y} 的关系若满足条件（1），则为多值函数。函数都是多值函数，但多值函数不都是函数。 X {\displaystyle X} 与 Y {\displaystyle Y} 的关系若满足条件（2），则为偏函数。函数都是偏函数，但偏函数不都是函数。除非特别指明，本条目中的“函数”总是指同时满足以上两个条件的关系。 考虑如下例子：

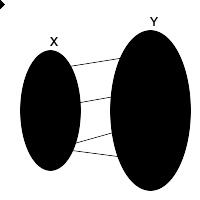
（1）一对多。X中的元素3与Y中的两个元素b和c相关。因此这是多值函数，而不是函数。（2）多对一或一对一。X的元素1未与Y的任一元素相关。因此这是偏函数，而不是函数。（3）完全对应且多对一，因此这是从X到Y的函数。此函数可以表示为f ={(1, d), (2, d), (3, c)}，或 f ( x ) = { d , if  x = 1 d , if  x = 2 c , if  x = 3 {\displaystyle f(x)=\left\{{\begin{matrix}d,&{\mbox{if }}x=1\\d,&{\mbox{if }}x=2\\c,&{\mbox{if }}x=3\end{matrix}}\right.}  

历史

函数这个数学名词是莱布尼兹在1694年开始使用的，用来描述跟曲线相关的一个量，如曲线的斜率或者曲线上的某一点。莱布尼兹所指的函数现在被称作可导函数，数学家之外的普通人一般接触到的函数即属此类。对于可导函数可以讨论它的极限和导数，此两者描述了函数输出值的变化同输入值变化的关系，是微积分学的基础。中文的“函数”一词由清朝数学家李善兰译出。其《代数学》书中解释：“凡此变数中函（包含）彼变数者，则此为彼之函数”。

1718年，约翰·伯努利（Johann Bernoulli）把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”

1748年，伯努利的学生欧拉（Leonhard Euler）在《无穷分析引论》一书中说：“一个变量的函数是由该变量和一些数或常量以任何一种方式构成的解析表达式”，例如 f ( x ) = sin ⁡ ⁡ --> ( x ) + x 3 {\displaystyle f(x)=\sin(x)+x^{3}} 。

1775年，欧拉在《微分学原理》一书中又提出了函数的一个定义：“如果某些量以如下方式依赖于另一些量，即当后者变化时，前者本身也发生变化，则称前一些量是后一些量的函数。”

19世纪的数学家开始对数学的各个分支进行形式化。维尔斯特拉斯（Karl Weierstrass）倡议将微积分学建立在算术，而不是几何的基础上，这种主张较趋向于欧拉的定义。

函数的定义得以扩展之后，数学家便能对一些“奇怪”的数学对象进行研究，例如处处不可导的连续函数。这些函数曾经被认为只具有理论价值，迟至20世纪初时它们仍被视作“怪物”。稍后，人们发现这些函数在对如布朗运动之类的物理现象进行建模时有重要的作用。

到19世纪末，数学家开始尝试利用集合论来进行数学的形式化。他们试图将每一个数学对象都定义为集合。狄利克雷（Johann Peter Gustav Lejeune Dirichlet）给出了现代正式的函数定义（参见下文#正式定义）。在他的定义作，函数被视作数学关系的特例。然而对于实际应用的情况，现代定义和欧拉定义的区别可以忽略不计。

单射、满射与双射函数

单射函数，将不同的输入值映射到不同的函数值。即：若x和y属于定义域，则仅当x = y时有f(x)= f(y)。

满射函数，其值域即为其到达域。即：对于映射f的到达域中之任意y，都存在至少一个x满足f(x)= y。

双射函数，既是单射的又是满射的函数。也叫一一对应、对射。双射函数经常被用于表明集合X和Y是等势的，即有一样的基数。如果在两个集合之间可以建立一个一一对应，则说这两个集合等势。

像和原像

元素x∈X在f之下的像就是ƒ(x)。

子集A⊂X在f之下的像，是以A的元素的像所组成的集合，为Y的一个子集，即

注意f的值域就是定义域X的像ƒ(X)。在#正式定义一节的最后例子中，{2,3}在f的像是ƒ({2, 3}) = {c, d}，而f的值域是{c, d}。

根据此定义，f可引申成为由X的幂集（由X的子集组成的集）到Y的幂集之函数，亦记作f。

子集B ⊂ Y在f的原像（或逆像）是如下定义的X的子集：

沿用同一例子，我们可以看到 {a, b} 的原像是ƒ({a, b}) = {}，即空集。

根据此定义，ƒ(x)是由Y的幂集到X的幂集之函数。

以下是f及f的一些特性：

ƒ(A1 ∪ A2) = ƒ(A1) ∪ ƒ(A2).

ƒ(A1 ∩ A2) ⊆ ƒ(A1) ∩ ƒ(A2).

ƒ(B1 ∪ B2) = ƒ(B1) ∪ ƒ(B2).

ƒ(B1 ∩ B2) = ƒ(B1) ∩ ƒ(B2).

ƒ(ƒ(B)) ⊆ B.

ƒ(ƒ(A)) ⊇ A.

这些特性适合定义域的任意子集A, A1及A2和到达域的任意子集B, B1及B2，甚至可推广到任意子集群的交集和并集。

函数图像

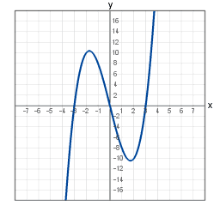
  立方函数的图像

函数f在平面上的图像是点对(x,f(x))的集合，其中x取遍定义域上的所有成员。函数图像可以帮助理解证明一些定理。 注意函数图像可以有两个定义：一是三元组（X,Y,G），其中X是函数的定义域，Y是函数的到达域，G是关系的图；二是索性以关系的图定义。用第二个定义则函数f等于其图象。

函数范例

首都之于国家（若不把多首都国[1]计算在内)。

每个自然数n的平方n²是n的函数。

对数函数。ln x是正实数x的函数。注意，虽然可以把对数函数推广到复数情况，但结果就不是函数了，而是多值函数。

对每个在 R 2 {\displaystyle \mathbb {R} ^{2}} 平面上的点，其和原点(0, 0)的距离是确定的。

常用的数学函数包括多项式函数、根式函数、幂函数、对数函数、有理函数、三角函数、反三角函数等。它们都是初等函数。非初等函数（或特殊函数）包括伽马函数和Bessel函数等。

函数的特性

函数可分为

奇函数或偶函数

连续函数或不连续函数

实函数或虚函数

标量函数或向量函数

单调增函数或单调减函数

分段函数

分段函数（Deutsch：Abschnittsweise definierte Funktion），在定义域内不同部分上，有不同的解析表达式，这样的函数通常叫分段函数。

复合函数

函数f: X → Y及g: Y → Z的复合函数是

举例，飞机在t时刻的高度是h(t)，而高度x处的氧气浓度是c(x)，则在t时刻飞机周围的氧气浓度是 (c o h)(t)

若Y⊂X则 f可自我复合；此时复合函数可记作f （不要与三角学的符号混淆）。函数的幂的定义是对自然数n有

反函数

对一个函数f: X→Y，若值域Y中任何一个元素y的原象是唯一的，那么这个函数就被称为是双射的。对任意的y∈Y到它的原象ƒ(y)的映射，我们称之为f的反函数，记为f。

举一个反函数的例子，比如ƒ(x) = x，它的反函数是ƒ(x) = √x。同样，2x的反函数是x/2。反函数是一个函数，它能够“抵消”它的原函数，并具有和原函数相同的单调性。参见逆映射。

函数的限制及扩张

给出 Y {\displaystyle Y} 的子集 X {\displaystyle X} 以及函数

则

称为 f {\displaystyle f} 在 X {\displaystyle X} 的限制。

反之，若给出函数

当一个定义在 Y {\displaystyle Y} 的函数 f : Y → → --> Z {\displaystyle f:Y\to Z} 有 f | X = g {\displaystyle f|_{X}=g} ， f {\displaystyle f} 就是 g {\displaystyle g} 的扩张。

点态运算

设函数f: X → R及g: X → R有X为共同的定义域及环R为共同的到达域。我们可以定义“函数和”f + g: X → R及“函数积”f×g：X → R如下：

对于所有X中的x。

这样子我们得出一个函数组成的环。这是一个抽象性扩张的例子，由此我们从较简单的结构得出更复杂的。

若然用别的代数结构A代替R，得出的由X到A的函数集会类似地拥有和A相同的代数结构。

歧义函数

歧义函数，也称多值函数，指有输出值多于一个的情况。例如，4的平方根可以是2或者-2，而两者的平方皆是4。

严格来说，歧义函数不完全算是函数，因为数学函数的定义对于一个输入值只能有唯一一个输出值。实际上，这样的“函数”通常被称为关系式。复变函数理论采用黎曼面处理函数多值的困境。

多元函数

多元函数（n-元函数）是指输入值为n-元组的函数。或者说，若一函数的输入值域为n个集合的笛卡尔积的子集，这函数就是n-元函数。例如，距离函数dist((x,y))是一个二元函数，输入值是由两个点组成的序对。另外，多复变函数（即输入值为复数的多元组）是一个重要的数学课题。

在抽象代数中，算子其实都是函数，如乘法"*"是个二元函数：当我们写x*y时，其实是用上了*(x,y)的中缀表示法。

函数式程序设计是一个以函数概念为中心的重要理论范式，其中的运算对象为多元函数，基本语法基于λ演算，而函数的复合则采用代换来完成。特别地，通过一种称为柯里化的变换，可将多元函数变换为一元函数。

可计算和不可计算函数

所有从整数到整数的可计算函数的个数是可数的，这是因为所有可能的算法个数是可数的。从整数到整数的函数个数要更多些－和实数个数一样多，也就是说是等势的。这说明有些从整数到整数的函数是不可计算的。关于不可计算函数，请参看停机问题和莱斯定理（英语：Rice"s theorem），OEIS中有一个经典的例子：A102288。

范畴论观点下的函数

在范畴论中，函数的槪念被推广为态射的槪念。

一个范畴包括一组物件与一组态射，每一个态射是个三元组(X, Y, f)，X称为源物件（定义域的类比），Y称为目标物件（到达域的类比），而源物件与目标物件是范畴内的物件。基于这种解释，可以把函数看作集合范畴里面的态射。

参考文献

Visual Calculusby Lawrence S. Husch,田纳西大学（2001年）

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。