发现

在哈勃做出他的观测之前10年，许多物理学家和数学家利用爱因斯坦广义相对论的场方程建立了时间和空间协调一致的理论。将最一般的原则应用到自然的宇宙，产生了一个动态的解决方案，与当时的静态宇宙的概念产生了冲突。

说明

因发现远离速度与距离呈线性关系，而产生哈勃定律，其线性数学式如后：

其中 v {\displaystyle v} 是由红移现象测得的远离速率，一般表示为km/s。 H 0 是哈勃常数，在弗里德曼方程中对应着数值 H {\displaystyle H} （通常称为哈勃参数，是一个取决于时间的值，由时间的观测得来，以下标 0 来区别。）此常数在宇宙中对任意保角时间（conformal time）而言皆是相同的。 D {\displaystyle D} 是光相对于观测者的惯性坐标系穿越星系的适当距离，以百万秒差距（Mpc）作为测量单位。

对于相对邻近的星系，速度 v 可从星系的红移 z 利用红移公式 v = z c {\displaystyle v=zc} 估计，其中 c 是光速。对遥远的星系，速度 v 可以从红移 z 利用相对移动的多普勒效应决定。然而，最好的方法来计算远离速度及其相关时空膨胀率是考虑来自远星系光子的相关保角时间。对于非常遥远的星体，退离速度可能大于光速。但是这并不违反狭义相对论，因为度量空间的扩张并不与任何有形物体的速度相关。

当使用哈勃定律来决定距离时，只能用因宇宙膨胀而造成的速度。引力相互作用星系的运行与彼此相关，而独立于宇宙膨胀之外。因其相对运行所造成的这类相对速度，被称作本动速度（ peculiar velocities ）。当使用哈勃定律时， 本动速度 需要加入考虑。1938年，Benjamin Kenneally所发现的“上帝的手指”效应（Fingers of God）是本动速度所造成的现象之一。受引力约束的系统，例如星系或我们的行星系统，都不会受到哈勃定律的影响，也不会膨胀。

针对均匀膨胀的宇宙的理想哈勃定律，其数学推导是一个在三维笛卡尔/牛顿协调空间相当初等的几何定理。此协调空间被视为一种度量空间，具有完全均匀和各向同性（性质不随地点或方向改变）。简单说明该定理如下：

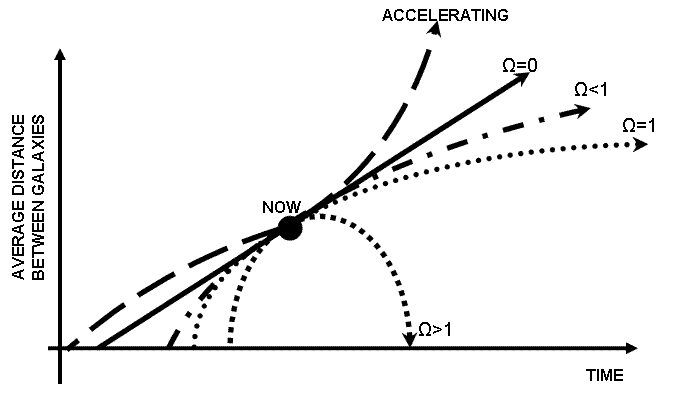
 宇宙的最终命运和宇宙的年龄，可以取决于测量现今的哈勃常数和推断减速参数的观测值，此参数特具密度参数值（Ω）的特征。所谓的“封闭宇宙”（Ω＞1）即将在一次“大紧缩”（Big Crunch）后结束，比哈勃年龄年轻。“开放宇宙”（Ω≦1）永远都在扩张且具有较接近哈勃年龄的年龄。我们所居住的宇宙为“加速宇宙”（accelerating universe），其年龄正巧非常接近哈勃年龄。

哈勃常数的值随着时间变化，其增加或减少取决于减速参数 q {\displaystyle q} 的正负， q {\displaystyle q} 定义为：

在减速参数为零的宇宙，有 H = 1/ t ，其中 t 是自大爆炸以来的时间。然而，非零且与时间相关的 q {\displaystyle q} 值，则需要积分弗里德曼方程，将时间倒退到粒子视野（particle horizon）为0时（即大爆炸之初）。

我们可以定义宇宙的“哈勃年龄”（又称为“哈勃时间”或“哈勃期”）为1/ H ，或9777.93（亿年/[ H /(km/s/Mpc)]）。哈勃年龄以 H =70 km/s/Mpc来计算为139.68亿年，或以 H =71 km/s/Mpc计算得137.72亿年。当星系的红移 z 很小时，与我们的距离大约是 zc / H ，其中 c 是1（光年／年），又此距离可以被简单地以 z （红移）时间表示为137.72亿光年。

长久以来 q 被认为是正值，这表示由于引力的作用，宇宙膨胀正在减慢。这意味着宇宙的年龄小于1/ H （约140亿年）。例如，若 q 为1/2时（其中一个理论上的可能值），宇宙的年龄为2/(3 H ) 。在1998年，一项发现指出 q 显然是负值，代表着宇宙其实比1/ H 还要老。事实上，估计的宇宙年龄相当接近1/ H 。

奥伯斯佯谬

哈勃定律对大爆炸的解释总结了空间的扩展与著名的古老难题奥伯斯佯谬之间的矛盾：如果宇宙是无限的、稳定的，充满了均匀分布的恒星，那么在天空中视线所及之处都将存在着恒星，而天空也将会像恒星的表面一样明亮。从1600年代开始，天文学家和其他的思想家提出了许多可能解决这个佯缪的想法，但当前能被接受的这一部分是来自大爆炸的理论。宇宙只存在了有限的时间，只有有限多的星光有机会到达我们这儿，所以矛盾就解决了。换言之，在膨胀的宇宙中，远方天体的远离速度使来自她们的星光产生红移并且降低了亮度，但这样也只是解决了部分的矛盾。依照大爆炸的理论，两者都有贡献（宇宙的历史是有限的在两者中较为重要）。 天空之所以黑暗，也为大爆炸提供了一种证据。

哈勃常数的测量

哈勃常数的值通常经由遥远星系的红移来测量，这就是用与哈勃定律不同的方法测量同一星系的距离。但是在用来测量这些距离的物理假设上的不确定，造成哈勃常数的值有不同结果的。在20世纪的后半期，多数的哈勃常数值 H 0 {\displaystyle H_{0}} 都被估计在50和 90 (km/s)/Mpc 之间。

对哈勃常数的争论

哈勃常数的值曾是个长久而激烈的争议主题，热拉尔·佛科留斯主张其值应为100而艾伦·桑德奇则认为其应为50附近 。

1996年，由约翰·诺利斯·巴寇主持，包含古斯塔夫·安德列斯·塔曼及薛尼·范德胡斯特以类似早期沙普利-柯蒂斯之争的模式举行，针对上述两个竞争数值进行辩论。

1990年代晚期，引进宇宙的λ-CDM模型，数值差异的问题获得部分的解决。

Λ-CDM 模型

在此模型下，利用苏尼亚耶夫-泽尔多维奇效应进行的X光高红移群及微波波长的观察、宇宙微波背景辐射各向异性的量度和光学调查皆测定哈勃常数的值为67左右。

使用哈勃太空望远镜的值

哈勃关键计划（由在卡内基天文台的Wendy L. Freedman博士主导）使用哈勃太空望远镜进行最精确的光学测量，在2001年五月 ，发表其最终估计值为72±8 (km/s)/Mpc，此结果与基于苏尼亚耶夫-泽尔多维奇效应进行的银河系星群观测所测出的 H 0 {\displaystyle H_{0}} 相当一致，具有相似的精确值。

使用WMAP的资料

在2003年，利用WMAP所得出最高精度的宇宙微波背景辐射测定值为71±4 (km/s)/Mpc，而在2006年，精确度提升至 70.4 +1.5 −1.6 (km/s)/Mpc ，2008年T，WMAP在线上提供的数值是 71.9 +2.6 −2.7 (km/s)/Mpc .[1]。 这些来自WMAP和其他宇宙论的数值都与简单版本的λ-CDM模型日趋接近。如果这些数值能与更普遍的版本吻合， H 0 {\displaystyle H_{0}} 倾向于更小和更不确定：通常数值在 67 ± 4 (km/s)/Mpc 的附近，但有些模型的数值接近63 (km/s)/Mpc 。

使用钱卓X射线天文台的资料

在2006年8月，来自马歇尔太空飞行中心（MSFC）的研究小组使用美国国家航空航天局的钱卓X射线天文台发现的哈勃常数是 77 (km/s)/Mpc ，误差大约是15% 。 所有这些测量方法结果的一致性，都支持 H 0 {\displaystyle H_{0}} 的值和ΛCDM模型。

膨胀的加速

在1998年，来自Ia超新星标准烛光测量的 q {\displaystyle q} 值却是负数，令许多天文学惊讶的是宇宙加速膨胀，虽然哈勃因子会随着时间而衰减。请参见暗物质和ΛCDM模型。

2009年5月7日，美国宇航局发布最新的哈勃常数测定值，根据对遥远星系Ia超新星的最新测量结果，常数被确定为74.2± 3.6 km/(s*Mpc)，不确定度进一步缩小到5%以内。

2012年10月3日，天文学家使用美国宇航局的斯皮策红外空间望远镜精确计算了哈勃常数，数值结果为74.3±2.1(km/s)/Mpc。

哈勃常数的推导

从弗里德曼方程开始：

此处 H {\displaystyle H} 是哈勃参数， a {\displaystyle a} 是宇宙标度因子， G {\displaystyle G} 是万有引力常数， k {\displaystyle k} 是标准化的宇宙空间曲率，其值为 −1、0、或 +1，和 Λ Λ --> {\displaystyle \Lambda } 是宇宙常数。

物质主导的宇宙(和宇宙常数)

如果宇宙是物质主导，则宇宙的质量密度 ρ ρ --> {\displaystyle \rho } 刚好可以包括的物质是

此处 ρ ρ --> m 0 {\displaystyle \rho _{m_{0}}} 是现在的物质密度，我们知道的非相对论粒子质量密度会随着宇宙的体积增加而成比例的降低，所以上述方程必须为真。我们也可以定义(参见 Ω Ω --> m {\displaystyle \Omega _{m}} 的密度参数)：

所以 ρ ρ --> = ρ ρ --> c Ω Ω --> m / a 3 . {\displaystyle \rho =\rho _{c}\Omega _{m}/a^{3}.} 也可以，依据定义：

和

此处的下标0代表现在的数值，并且 a 0 = 1 {\displaystyle a_{0}=1} 。到此为止的所有一切都是章节刚开始的弗里德曼方程和转换 a {\displaystyle a} 成为 a = 1 / ( 1 + z ) {\displaystyle a=1/(1+z)} 得到

物质和暗能量主导的宇宙

如果宇宙是物质主导和暗能量主导，然后前述方程中的哈勃参数也将是暗能量的状态方程。所以现在：

此处 ρ ρ --> d e {\displaystyle \rho _{de}} 是暗能量的质量密度。依据定义，在宇宙论的状态方程是 P = w ρ ρ --> c 2 {\displaystyle P=w\rho c^{2}} ，并且我们将这带入流体的方程，它描述了宇宙的质量密度随着时间的变化，

如果w 是常数，

那么暗能量就是w状态的恒等式， ρ ρ --> d e ( a ) = ρ ρ --> d e 0 a − − --> 3 ( 1 + w ) {\displaystyle \rho _{de}(a)=\rho _{de0}a^{-3\left(1+w\right)}} 。如果我们以与之前相似的方式转换弗里德曼方程，但是这次设定 k = 0 {\displaystyle k=0} ，这是假设我们生活在一个平坦宇宙的形状 (参见宇宙的形状)，

如果暗能量不是w状态的恒等式，则

要解此方程，我们需要参数化 w ( a ) {\displaystyle w(a)} ，例如如果 w ( a ) = w 0 + w a ( 1 − − --> a ) {\displaystyle w(a)=w_{0}+w_{a}(1-a)} ，得到

由哈勃常数导出的单位

哈勃时间

哈勃常数 H 0 {\displaystyle H_{0}} 的单位是时间的倒数，也就是说 H 0 {\displaystyle H_{0}} ~ 2.29×10 s 。“哈勃时间”定义为 1 / H 0 {\displaystyle 1/H_{0}} 。在标准宇宙论模型的哈勃时间是4.35×10 s 或138亿年（Liddle 2003，p.57），"扩张时间尺度"一词的意思是"哈勃时间"[2]。如果 H 0 {\displaystyle H_{0}} 的值保持恒定，哈勃时间自然的解释是电子大小的宇宙增加一个数量级所需要的时间 (因为解dx/dt = x H 0 {\displaystyle H_{0}} is x = s 0 {\displaystyle s_{0}} exp( H 0 {\displaystyle H_{0}} t)，此处 s 0 {\displaystyle s_{0}} 是在t = 0的任意初始条件下的形状)。但是，在如上文所述的广义相对论、暗能量、暴胀等，长时间下的动力学是复杂的。

哈勃长度

哈勃长度是宇宙论的距离单位，定义为 c / H 0 {\displaystyle c/H_{0}} —光速与哈勃时间的乘积。它相当于42亿2800万秒差距或138亿光年(哈勃长度以光年表示的数值，依据定义，等同于哈勃时间以年表示的值)。

哈勃体积

哈勃体积有时被定义为共动大小 c / H 0 {\displaystyle c/H_{0}} 的体积。精确的定义是：有时将其定义为球体半径为 c / H 0 {\displaystyle c/H_{0}} 时的体积。有些宇宙论甚至使用哈勃体积一词引用为可观测宇宙的体积，然而这个半径可能还要大3倍。

相关条目

宇宙的年龄

宇宙形状

参考资料

Kutner, Marc. Astronomy: A Physical Perspective. Cambridge University Press. 2003. ISBN 978-0-521-52927-3.

Hubble, E.P.., The Observational Approach to Cosmology (Oxford, 1937)

ticle/436836/

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。