ℝ³ 上的斯托克斯公式

设S是分片光滑的有向曲面，S的边界为有向闭曲线Γ，即Γ Γ -->=∂ ∂ -->S{\displaystyle \Gamma =\partial S}，且Γ的正向与S的侧符合右手规则： 函数P(x,y,z)、Q(x,y,z)、R(x,y,z)都是定义在“曲面S连同其边界Γ”上且都偏导数阶连续偏导数的函数，则有

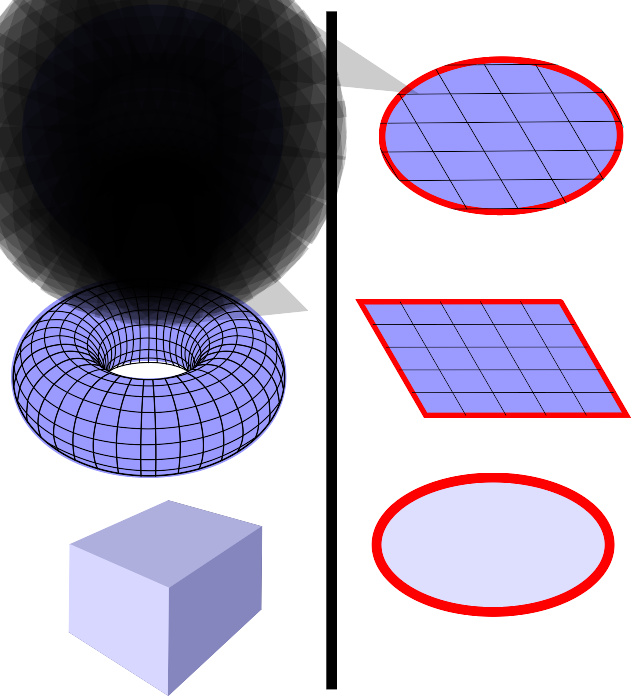
旋度定理可以用来计算穿过具有边界的曲面，例如，任何右边的曲面；旋度定理不可以用来计算穿过闭曲面的通量，例如，任何左边的曲面。在这图内，曲面以蓝色显示，边界以红色显示。

这个公式叫做 ℝ³ 上的斯托克斯公式或开尔文－斯托克斯定理、旋度定理。这和函数的旋度有关，用梯度算符可写成：

它将ℝ³ 空间上“向量场的旋度的曲面积分”跟“向量场在曲面边界上的线积分”之间建立联系，这是一般的斯托克斯公式（在 n=2 时）的特例，我们只需用ℝ³ 空间上的内积把向量场看作等价的1-形式。该定理的第一个已知的书面形式由威廉·汤姆森（开尔文勋爵）给出，出现在他给斯托克斯的信中。

类似的，高斯散度定理

也是一般的斯托克斯公式的一个特例，如果我们把右边的 F⋅ ⋅ -->dS{\displaystyle \mathbf {F} \cdot d\mathbf {S} } 看成是等价的(n-1)-形式，可以通过和体积形式的内积实现。微积分基本定理和格林定理也是一般性斯托克斯定理的特例。使用微分形式的一般化斯托克斯定理当然比其特例更强，虽然后者更直观而且经常被使用它的科学工作者或工程师认为更方便。

另一种形式

通过以下公式可以在对坐标的“曲线积分”和对面积的“面积积分”之间相互转换：

流形上的斯托克斯公式

令 M 为一个可定向分段光滑 n 维流形，令 ω 为 M 上的 n−1 阶 C 类紧支撑微分形式。如果 ∂M 表示 M 的边界，并以 M 的方向诱导的方向为边界的方向，则

这里 dω 是 ω 的外微分, 只用流形的结构定义。这个公式被称为一般的斯托克斯公式（generalized Stokes" formula），它被认为是微积分基本定理、格林公式、高－奥公式、ℝ³ 上的斯托克斯公式的推广；后者实际上是前者的简单推论。

该定理经常用于 M 是嵌入到某个定义了 ω 的更大的流形中的子流形的情形。

定理可以简单的推广到分段光滑的子流形的线性组合上。斯托克斯定理表明相差一个恰当形式的闭形式在相差一个边界的链上的积分相同。这就是同调群和德拉姆上同调可以配对的基础。

应用

斯托克斯公式是格林公式的推广。

利用斯托克斯公式可计算曲线积分。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。