圆面积公式

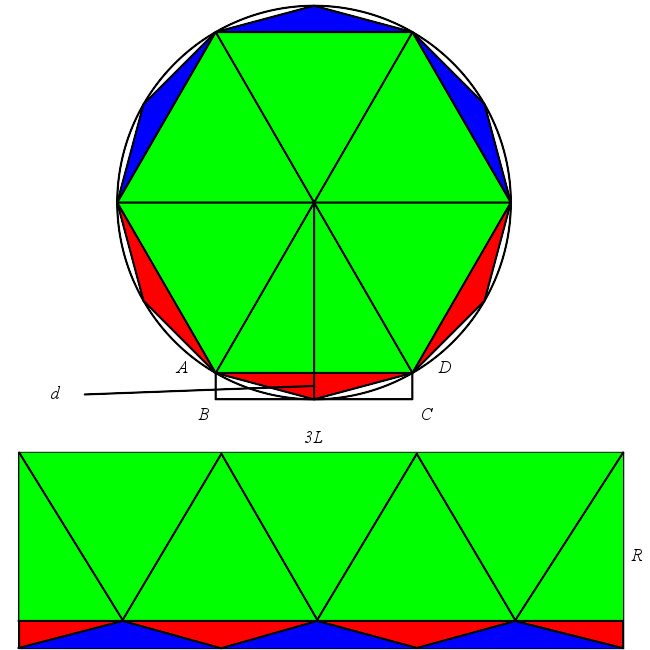
圆面积=圆的半周长X半径

刘徽割圆术是建立在圆面积论的基础之上的。他首先论证，将圆分割成多边形，分割来越细，多边形的边数越多，多边形的面积就和圆面积没有差别了。他说，将6边形一边的长度乘以圆半径，再乘3，得12边形的面积。将12边形的一边长乘半径，再乘6，得24边形面积。越割越细，多边形和圆面积的差越小。如此割了再割，最后终于和圆合为一体，毫无差别了 。

刘徽明显已经掌握了无穷小分割和极限的概念：

显然，刘徽之所以研究余径，目的是从上限和下限两个方面逐步逼近圆面积：

刘徽进一步证明圆面积=圆周/2 × 半径。

割圆术程序

刘徽从半径1尺圆的内接正6边形开始，逐次分割为12边形，24边形，48边形，96边形。反复使用勾股定理求得各多边形的边长，又用刘氏多边形面积公式求多边形面积。

分割6边形为12边形

刘徽割圆术原理

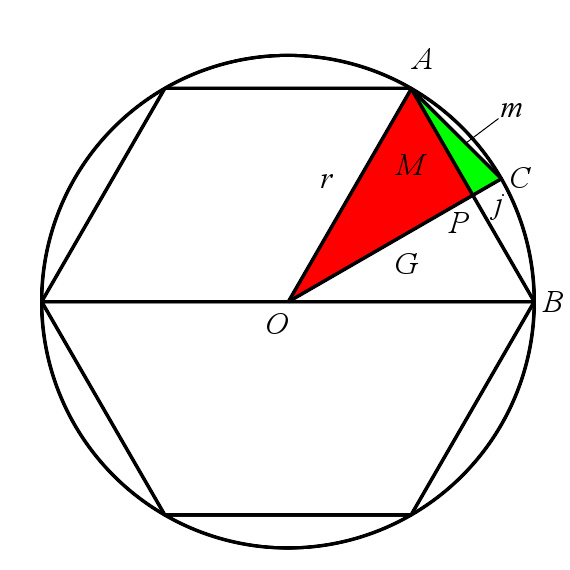
令圆直径为2尺，折半得半径1尺。圆内接正6边形的边长也是1尺。 如图：

OAP是一个直角三角形

APC是一个小直角三角形

令小弦AC长度为m，令小句PC长度为j

分割12边形为24边形

将上一轮的多边形边长m作为新一轮割圆的开始， 作替换M=m=12边形的一边长度 = 517638.09 {\displaystyle =517638.09} 忽 继续将此多边形的一边平分，周而复始，重复使用 ：

分割24边形为48边形

将第二轮的多边形边长m作为第三轮割圆的起点 ， 作替换 M = m = 261052 2 5 {\displaystyle M=m=261052{2 \over 5}}

根据刘徽多边形面积公式：

所以96边形的面积 A 96 = 130806 × × --> 48 2 × × --> 1000000 {\displaystyle A_{96}=130806\times {\frac {48}{2}}\times 1000000}

分割48边形为96边形

将第三轮的多边形边长m作为第四轮割圆的起点

作替换 M = m = 130806 {\displaystyle M=m=130806} 忽

根据刘徽多边形面积公式：

所以192边形的面积 A 192 = 65438 × × --> 96 2 × × --> 1000000 {\displaystyle A_{192}=65438\times {\frac {96}{2}}\times 1000000} 平方忽

刘徽圆周率不等式

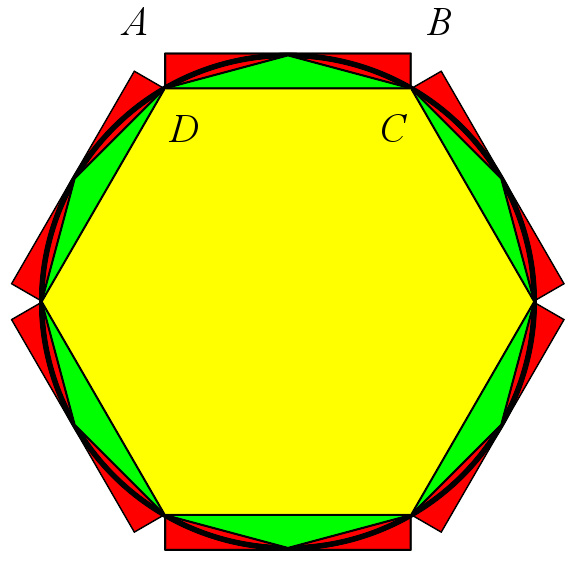
刘徽圆周率不等式示意图

刘徽利用多边形面积差的几何学，得出圆周率的双边不等式。

或

当N=96，2N=192：

刘徽认为这个面积已经超过圆面积，所以将192边形的面积的整数部分定为圆面积：

这就是徽率。

实际上只要计算精确度够高，刘徽割圆术可以计算到任何精确度，不仅限于二位小数点。

圆周率捷法

刘徽在得圆周率=3.14之后，将这个数值和晋武库中汉王莽时代制造的铜制体积度量衡标准嘉量斛的直径和容积检验，发现3.14这个数值还是偏小。于是继续割圆到1536边形，求出3072边形的面积，得到令自己满意的圆周率 = 3927 1250 = 3.1416 {\displaystyle ={3927 \over 1250}=3.1416} 。但是刘徽却不叙述“分割96边形为192边形”，“分割192边形为384边形”，“分割384边形为768边形”，“分割768边形为1536边形”：因为他发现了一个快捷的算法 ，只要利用96边形的数据经过一次除法和一次加法，就可以获得和计算到1536边形同等的精确度 π π --> = 3.1416 {\displaystyle \pi =3.1416} ，省去了4次开方计算；三国在三国筹算用筹算进行开方相当的繁难。

刘徽圆周率捷法乃是以他素有研究的多边形面积差为基础的。

D 2 N = A 2 N − − --> A N {\displaystyle D_{2N}=A_{2N}-A_{N}}

其中

刘徽圆周率捷法，可以解释如下几个问题：

刘徽的 π π --> {\displaystyle \pi } = 3927 1250 {\displaystyle 3927 \over 1250} 后印度于印度数学中，足证古印度数学采用刘徽注《九章算术》

割圆术迭代公式

如令半径=1， 从

可简化为：

π的连平方根表示式

根据刘徽割圆术迭代公式：

从半径=1的内接6边形开始：

半径=1圆形正内接多边形面积：

祖率

南北朝数学家祖冲之，并没有发明新的方法计算圆周率 ，而是将刘徽割圆术的计算，继续分割到12288边形，又用刘徽多边形面积公式，求得24576边形的面积：

再用刘徽圆周率不等式：

取八位有效数字即得祖冲之著名的圆周率不等式：

祖冲之算得的圆周率准确到小数点后7位，保持了世界最准确圆周率达900年之久。祖冲之熟悉何承天调日法，以3为弱率， 以4为强率，通过调日法计算7次得圆周率约率 22 7 > π π --> {\displaystyle {22 \over 7}>\pi } ，计算23次得密率 355 113 > π π --> {\displaystyle {355 \over 113}>\pi } 。

根据调日法计算出来的约率和密率都是强率；所谓约率只意味这个数值和圆周率的误差较大，并无约率“小于”圆周率的意思。

和阿基米德割圆术比较

希腊数学家阿基米德用阿基米德割圆术计算圆周率，他的论证以计算线长为依据，在推导过程中不考虑多边形面积面积，和刘徽的以面积计算为中心的割圆术成对照。他用两套不同的方法方法，先多次分割圆的切线，证明π> 223 71 {\displaystyle {223 \over 71}} ；另用内接多边形，计算到96边形，证明π< 22 7 {\displaystyle {22 \over 7}} ，从而得到不等式

刘徽得到的圆周率弱值3.141024和强值3.142704都比阿基米德准确 。

参见

赵友钦割圆术

注释

^吴文俊《中国数学史大系》第三卷 367页

^ “增周太多，过其实矣”

^ “此术微小”

^ 以六觚之一面乘半径，因而三之，得十二觚之幂(中国古代数学文献中 幂 指几何图形的面积)。若又割之，次以十二觚之一面乘半径，因而六之，则得二十四觚之幂。割之弥细，所失弥少。割之又割，则与园合体，而无所失矣。”《九章算术》第一卷 方田 刘徽注

^ 最先指出这一点的日本数学史家三上义夫

^ 觚面之外，犹有余径，以面乘余径，则幂出觚表，若夫觚之细者，与圆合体，则表无余径。表无余径则幂不出外矣。以一面乘半径，觚而裁之，每辄自倍。”

^ 刘徽注：“故以半周乘半径而为圆幂”。

^ 刘徽原文： 术曰：“置圆径二尺，半之为一尺，即圆里觚之面也。令半径一尺为弦，半面五寸为句，为之求股。以句幂二十五寸减弦幂，余七十五寸，开方除之下至秒忽，又一退法，求其微数。微数无名，知以为分子，以下为分母，约作五分忽之二，故得股八寸六分六厘二秒五忽五分忽之二。以减半径，余一寸三分三厘九毫七秒四忽五分忽之三，谓之小句。觚之半面，又谓之小股，为之求弦。其幂二千六百七十九亿四千九百一十九万三千四百四十五忽，余分弃之。开方除之，即十二觚之一面也。”

^ 三国时代还没有发明小数点，而用分数表示个位以下的数

^ 刘徽原文： 术曰：“亦令半径为弦，半面为句，为之求股。置上小弦幂，四而一，得六百六十九亿八千七百二十九万八千三百六十一忽，余分弃之，即句幂也。以减弦幂，其余开方除之，得股九寸六分五厘九毫二秒五忽五分忽之四。以减半径，余三分四厘七秒四忽五分忽之一，谓之小句。觚之半面又谓之小股。为之求小弦。其幂六百八十一亿四千八百三十四万九千四百六十六忽，余分弃之。开方除之，即二十四觚之一面也。”

^ 刘徽原文： 术曰：“亦令半径为弦，半面为句，为之求股。置上小弦幂，四而一，得一百七十亿三千七百八万七千三百六十六忽，余分弃之，即句幂也。以减弦幂，其余，开方除之，得股九寸九分一厘四毫四秒四忽五分忽之四。以减半径，余八厘五毫五秒五忽五分忽之一，谓之小句。觚之半面又谓之小股。为之求小弦。其幂一百七十一亿一千二十七万八千八百一十三忽，余分弃之。开方除之，得小弦一寸三分八毫六忽，余分弃之，即四十八觚之一面”。

^ 刘徽原文： 术日：“亦令半径为弦，半面为句，为之求股。置次上弦幂，四而一，得四十二亿七千七百五十六万九千七百三忽，余分弃之，则句幂也。以减弦幂，其余，开方除之，得股九寸九分七厘八毫五秒八忽十分忽之九。以减半径，余二厘一毫四秒一忽十分忽之一，谓之小句。觚之半面又谓之小股。为之求小弦。其幂四十二亿八千二百一十五万四千一十二忽，余分弃之。开方除之，得小弦六分五厘四毫三秒八忽，余分弃之，即九十六觚之一面。”

^ 最早由日本数学史家三上义夫提出

^ 《李俨.钱宝琮科学史全集》卷9 396页

^ 清阮元撰《畴人传》：“后祖冲之更创密法，仍是割之又割耳，未能于徽注之外，别立新术也”

^吴文俊主编《中国数学史大系》第二卷 219页

^ 阿基米德原著 《量圆》 《中国数学史大系》 副卷第一 第二章 第三编 希腊 197-203页

^ 阿基米德原著 《量圆》 《中国数学史大系》 副卷第一 第二章 第三编 希腊 203页

^ 阿基米德原著 《量圆》 《中国数学史大系》 副卷第一 第二章 第三编 希腊 203页

延伸阅读

《九章算术》

吴文俊主编 《中国数学史大系》第三卷 第一章第三节 刘徽的割圆术 152-164页 ISBN 7-303-04557-0

傅海伦编著 《中外数学史概论》 第四章 第三节 刘徽的割圆术 49-52页 ISBN 987-7-03-018477-1

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。