历史

李冶《益古演段》中的天元术

朱世杰《算学启蒙》中的天元术

伟烈亚力《中国数学科学札记》论天元术

在中国数学史上最早创立天元概念的是北宋平阳蒋周所著的《益古集》，随后有博陆李文一撰《照胆》，鹿泉石信道撰《钤经》，平水刘汝谐撰《如积释锁》，处州李思聪《洞渊九容》后人才知道有天元。

李冶在东平获得刘汝谐撰《如积释锁》，书中用十九个单字表示未知数的各个 x 9 {\displaystyle x^{9}} 至 x − − --> 9 {\displaystyle x^{-9}} 的幂：

后来有太原彭泽彦出，反其道而行，以天元在下 。

《益古集》，《照胆》，《钤经》，《如积释锁》，《洞渊九容》等早期天元术著作今已失传。李冶在《测圆海镜》中使用天元在上的天元术。后来李冶又著《益古演段》，采用天元在下的次序。朱世杰《四元玉鉴》和《算学启蒙》卷下也采用天元在下的次序。

例子

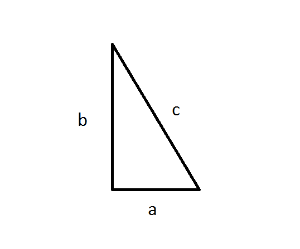
a 勾 b 股 c 弦

在天元术中，一次项系数旁记一“元”字（或在常数项旁记一“太”字）。

“元”以上的系数表示各正次幂，“元”以下的系数表示常数项和各负次幂）。

例：李冶《测圆海镜》第二卷第十四问方程： − − --> x 2 − − --> 680 x + 96000 = 0 {\displaystyle -x^{2}-680x+96000=0}

“元”以下的系数表示各正次幂，“元”以上的系数表示常数和各负次幂

例一：

李冶《益古演段》卷中第三十六问中的方程= 3 x 2 + 210 x − − --> 20325 {\displaystyle 3x^{2}+210x-20325} 用天元术表示为:

其中“太”是常数项，算筹 打斜线表示该项常数为负数。 “元”相当于未知数x

例二：

朱世杰《算学启蒙》下卷第四问

将代数方程

( 92 − − --> X ) X − − --> 2052 = 0 {\displaystyle (92-X)X-2052=0}

表示为天元方程：

例三：

朱世杰《四元玉鉴》《一气混元》

根据条件 黄方乘直积得二十四步

b + c = 9 {\displaystyle b+c=9} x = a {\displaystyle x=a} (立天元一为勾) 由此得方程

x 5 − − --> 9 x 4 − − --> 81 x 3 + 729 x 2 = 3888 {\displaystyle x^{5}-9x^{4}-81x^{3}+729x^{2}=3888}

解之，得勾=3

天元术与阿拉伯代数之差异

天元术与阿拉伯代数虽功用相同，但方法迥异。天元术可解高次方程，阿拉伯代数只能解一次，二次方程。天元术解根只求正根，但阿拉伯代数解二次方程得二根。

参见

《益古演段》 《算学启蒙》 《四元玉鉴》

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。