近似值

《周髀算经》：“径一周三”，即π=3。

由刘徽给出的 徽率 ：3.14 ( 157 50 {\displaystyle {\tfrac {157}{50}}} )。

张衡： 10 {\displaystyle {\sqrt {10}}} 。

由祖冲之给出的 约率 ：22 7 {\displaystyle {\tfrac {22}{7}}}及 密率 ：355 113 {\displaystyle {\tfrac {355}{113}}} 。

六十进制的圆周率数值约为：

2143 22 4 {\displaystyle {\sqrt[{4}]{\tfrac {2143}{22}}}} ，求得3.141592653...。

π的首一千个小数位如下 (数列A000796)：

发展历史

一块产于公元前1900年的古巴比伦石匾清楚地记载了圆周率 = 25 8 = 3.125 {\displaystyle ={\tfrac {25}{8}}=3.125} 。同一时期的古埃及文物也表明圆周率等于分数 ( 16 9 ) 2 {\displaystyle \left({\tfrac {16}{9}}\right)^{2}} ，约等于3.16。埃及人似乎在更早的时候就知道圆周率了。英国作家 John Taylor (1781–1864) 在其名著《金字塔》中指出，造于公元前2500年左右的金字塔和圆周率有关。例如，金字塔的周长和高度之比等于圆周率的两倍，正好等于圆周和半径之比。公元前800至600年成文的古印度宗教巨著《百道梵书》（Satapatha Brahmana）显示了圆周率等于分数 339 108 {\displaystyle {\tfrac {339}{108}}} , 约等于3.139。

古希腊作为古代几何王国对圆周率的贡献尤为突出。古希腊大数学家阿基米德(公元前287–212 年) 开创了人类历史上通过数学算法计算圆周率近似值的先河。

计算及发展

由于π的无理性，所以只能以近似值的方法计算π。对于一般应用3.14或 22 7 {\displaystyle {\tfrac {22}{7}}} 已足够，但工程学常利用3.1416（5位有效数字）或3.14159（6位有效数字）。至于密率 355 113 {\displaystyle {\tfrac {355}{113}}} （3.1415929...）则是一个易于记忆（三个连续奇数：113355），且精确至7位有效数字的分数近似值。

而在2009年末，有科学家已经用超级计算机计算出圆周率小数点后2兆7千亿个小数位。

而在2010年8月，日本男子近藤茂利用自己组装硬盘容量达32TB的计算机，计算出圆周率小数点后5兆个小数位。

而在2011年10月19日，日本程序员JA0HXV宣布他已经将圆周率Pi计算到小数点后10兆位。

实验时期

公元前17世纪的埃及古籍《阿美斯纸草书》（ Ahmes ，又称“阿梅斯草片文书”；为英国人Alexander Henry Rhind（莱因德）于1858年发现，因此还称“莱因德数学纸草书”（Rhind Mathematical Papyrus））是世界上最早给出圆周率的超过十分位的近似值，为256/81 ( = 3 + 1/9 + 1/27 + 1/81)或3.160。这部纸草书声称是抄自300年前的另一部文献，也就是说，这个Pi值是公元前1850年（1850 BC）就存在了。

在阿基米德以前，π值的测定依靠实物测量。

几何法时期——反复割圆

阿基米德用正96边形割圆术得出圆周率介于 3 1 7 {\displaystyle 3{\tfrac {1}{7}}} 与 3 10 71 {\displaystyle 3{\tfrac {10}{71}}} 之间。

中国古籍云：“径一周三” ，意即取π=3。

公元263年，中国数学家刘徽用“割圆术”计算圆周率，他先从圆内接正六边形，逐次分割为12、24、48、96、192边形。他说“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”（分割愈精细，误差愈少。分割之后再分割，直到不能再分割为止，它就会与圆周完全重叠，就不会有误差了），其中有求极限的思想。刘徽给出π=3.141024的圆周率近似值，并以 157 50 = 3.14 {\displaystyle {\tfrac {157}{50}}=3.14} （徽率）为其分数近似值。刘徽求得该近似值之后，将这个数值和晋武库中汉王莽时代制造的铜制体积度量衡标准嘉量斛的直径和容积检验，发现3.14这个数值还是偏小 。于是继续割圆到1536边形，求出3072边形的面积，得到令自己满意的圆周率 = 3927 1250 = 3.1416 {\displaystyle ={\tfrac {3927}{1250}}=3.1416} 。其后印度数学家阿耶波多于公元499年得到圆周率 = 62832 20000 = 3.1416 {\displaystyle ={\tfrac {62832}{20000}}=3.1416} ，与刘徽给出的近似值一样，不过分子和分母是刘徽的十六倍。

公元466年，中国数学家祖冲之将圆周率算到小数点后7位的精确度及计算至正24576边形，这一纪录在世界上保持了一千年之久。同时，祖冲之给出了 355 113 {\displaystyle {\tfrac {355}{113}}} （密率）这个很好的分数近似值，它是分母小于16604的分数中最接近π的 。（参见有理逼近）。为纪念祖冲之对圆周率发展的贡献，日本数学家三上义夫将这一推算值命名为“祖冲之圆周率”，简称“祖率”。可惜祖冲之的著作《缀术》已经亡佚，后人无从得知祖冲之如何估算圆周率的值。

钱大昕的《十驾斋养新录》卷第十七首条〈圆径周率〉引《隋书律历志》：“古之九数，圆周率三圆径率一，其术疏舛，自刘歆、张衡、刘徽、王蕃、皮延宗之徒，各设新率，未臻折衷。宋末南徐州从事史祖冲之更开密率，以圆径一亿为一丈，圆周盈数三（刻本作二，误）丈一尺四寸一分五釐九毫二秒七忽，朒数三丈一尺四寸一分五釐九毫二秒六忽，正数在盈朒二限之间，密率圆径一百一十三，圆周三百五十五，约率圆径七，周二十二。又设开差幂、开差立，兼以正圆参之，指要精密，算氏之最者也。”

清末大臣曾国藩之子曾纪鸿与左潜于1874年曾计算出圆周率值到100位，合著《圜率考真图解》记载计算方法。

分析法时期

这一时期人们开始摆脱利用割圆术的繁复计算，开始利用无穷级数、无穷乘积或极限求π。

鲁道夫·范·科伊伦（约1600年）计算出π的小数点后首35位。他对此感到自豪，因而命人把它刻在自己的墓碑上。

斯洛文尼亚数学家Jurij Vega于1789年得出π的小数点后首140位，其中只有137位是正确的。这个世界纪录维持了五十年。他利用了John Machin于1706年提出的数式。

所有以上的方法都不能快速算出π。第一个快速算法由数学家梅钦在1706年提出：

其中arctan( x )可由泰勒级数算出。类似方法称为“梅钦类公式”。

另一个快速算法如下：

上述方法利用分析学的定义： π π --> {\displaystyle \pi \,} 为满足 sin ⁡ ⁡ --> ( x ) = 0 {\displaystyle \sin(x)=0\,}实数的最小正实数 x {\displaystyle x\,} 求 π π --> {\displaystyle \pi \,} 。

计算机时代

上万位以上的小数位值通常利用高斯-勒让德算法或波温算法；另外以往亦曾使用于1976年发现的萨拉明-布伦特算法。

第一个π和1/π的小数点后首一百万位利用了古腾堡计划。最新纪录是2002年9月得出的1,241,100,000,000个小数位，由拥有1TB主内存的64-node日立超级计算机，以每秒200亿运算速度得出，比旧纪录多算出一倍（206亿小数位）。此纪录由以下梅钦类公式得出：

实际上生活中我们也用不到这么多位数，但这有助于超级计算机的测试。(参见高精度π的应用)

1996年，David H. Bailey、Peter Borwein及西蒙·普劳夫发现了π的其中一个无穷级数：

以上述公式可以计算π的第 n 个二进制或十六进制小数，而不需先计算首 n -1个小数位。此类π算法称为贝利－波尔温－普劳夫公式。请参考Bailey"s website 上相关程序。

法布里斯·贝拉于1997年给出了计算机效率上高出上式47%的BBP算法：

请参考Fabrice Bellard"s PI page。

其他计算圆周率的公式包括：

编写计算机程序时，也可以利用反三角函数直接定义 π π --> {\displaystyle \pi } 值，但是编译器必三角函数角函数的函式库：

利用正弦函数

利用余弦函数

计算机代数系统

多种计算机代数系统软件都可以计算高精度圆周率。

例如Maple

evalf(Pi,100000)

现在的 AMD Althon x8 处理器电脑上20秒内算出一百万位圆周率数值。

年表

用梅钦公式编程计算圆周率(C++

#include#includeusingnamespacestd;intmain(void){//本程序为每四位数输出，如果请求计算的位数不是4的整数倍，最后输出可能会少1~3位数longa[2]={956,80},b[2]={57121,25},i=0,j,k,p,q,r,s=2,t,u,v,N,M=10000;printf("%9cMachin%6cpi=16arctan(1/5)-4arctan(1/239)\nPlease input a number.\n",32,32);cin>>N,N=N/4+3;long*pi=newlong[N],*e=newlong[N];while(i<N)pi[i++]=0;while(--s+1){for(*e=a[k=s],i=N;--i;)e[i]=0;for(q=1;j=i-1,i<N;e[i]?0:++i,q+=2,k=!k)for(r=v=0;++j<N;pi[j]+=k?u:-u)u=(t=v*M+(e[j]=(p=r*M+e[j])/b[s]))/q,r=p%b[s],v=t%q;}while(--i)(pi[i]=(t=pi[i]+s)%M)<0?pi[i]+=M,s=t/M-1:s=t/M;for(cout<<"3.";++i<N-2;)printf("%04ld",pi[i]);delete[]pi,delete[]e,cin.ignore(),cin.ignore();return0;}

用级数编程计算圆周率(C++)

#include#includeusingnamespacestd;intmain(void){longb=1000,c=200,d=0,e,f,i=0,N;cout<>N,N=N*10/3+20;long*a=newlong[N+1];while(i0;printf("%03ld",d+=(c+=e/b)/b),d=c%b,c=e%b)for(e=0,i=N;--i;a[i]=(e+=a[i]*b)%(f=i*2+1),e=e/f*i);delete[]a,cin.ignore(),cin.ignore();return0;}

特性和相关公式

几何

环面的体积和表面积公式

R是管子的中心到环面的中心的距离， r是圆管的半径。

代数

π是个无理数，即不可表达成两个整数之比，是由朗伯于1761年证明的。 1882年，林德曼更证明了π是超越数，即不可能是任何有理数多项式的根。

圆周率的超越性否定了化圆为方这古老尺规作图问题的可能性，因所有尺规作图只能得出代数数，而超越数不是代数数。

数学分析

π有个特别的连分数表示式：

π本身的连分数表示式(简写)为[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,...]，其近似部分给出的首三个渐近分数

第一个和第三个渐近分数即为约率和密率的值。数学上可以证明，这样得到的渐近分数，在分子或分母小于下一个渐进分数的分数中，其值是最接近精确值的近似值。

(另有12个表达式见于[2])

欧拉恒等式

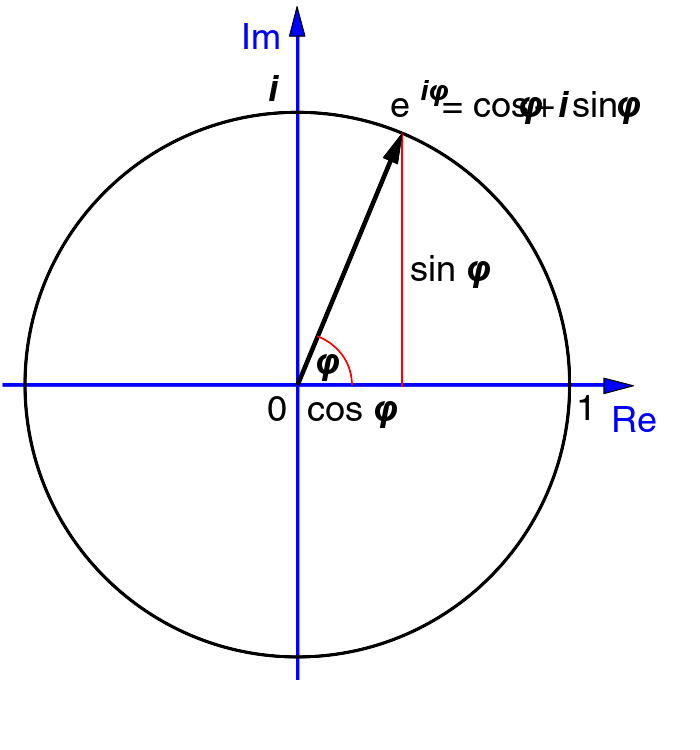
欧拉公式（Euler"s Formula）给出了 e 的复指数与复平面（Complex Plane）上以原点（Origin）为圆心的单位圆（Unit Circle）上的点之间的关系。

任何复数（Complex Number）（以 z 为例）都可以表示为一组实数（Real Number）对：在极坐标系（Polar Coordinate System）中，一个实数 r ——半径（Radius）代表复平面（Complex Plane）上复数 z 离原点（Origin）的距离，另一个实数 φ ——夹角表示这条半径（复平面上复数 z 与原点的连线）与正实轴经顺时针转动的夹角，这样就可以写成

在复分析（Complex Analysis）中，欧拉公式（Euler"s Formula）联系着三角函数（Trigonometric Function）与复指数函数（Exponential Function） ：

欧拉公式确立了 e 的复指数与复平面上以原点为圆心的单位圆（Unit Circle）上的点之间的关系，而且当我们令 φ = π 时，欧拉公式就能改写为欧拉恒等式（Euler"s Identity）的形式：

方程 z = 1 共有 n 不同的复数根，这些根被称为“ n 次单位根（Root of Unity）” ，可以根据以下公式求得：

数论

蒙特卡洛方法

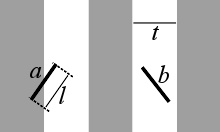
布丰投针问题（Buffon"s needle），多枚长度为 ℓ 的针随机地抛掷向平面。 随机地往内切四分之一圆的正方形内抛掷大量的点。 蒙特卡罗方法（Monte Carlo methods）基于随机试验结果计算 π 的近似值

蒙特卡罗方法（Monte Carlo Methods）是以概率统计理论为指导的一类非常重要的数值计算方法，通过进行大量重复试验计算事件发生的频率，利用当试验次数充分大时频率充分地接近于概率可以求得 π 的近似值 。布丰投针问题（Buffon"s Needle）就是其中一个应用的例子：当一枚长度为 ℓ 的针随机地往一个画满间距为 t ( ℓ ≤ t ) 的平行线的平面上抛掷 n 次， 如果针与平行直线相交了 m 次，那么当 n 充分大时就可根据以下公式算出 π 的近似值 ：

另一个利用蒙特卡罗方法计算 π 值的例子是随机地往内切四分之一圆的正方形内抛掷大量的点，落在四分之一圆内的点的数量与抛掷点的总量的比值会近似等于 π/4 .

File:Five random walks.png 五次200步的随机游走试验， | W 200 | 的样本均值为 μ = 56/5 ，因此可以算得 π 的近似值为 2×200μ ≈ 3.19 ，偏差为 0.05 以内

另一个利用蒙特卡罗方法计算 π 值的例子是进行随机游走（Random Walk）试验，如多次抛掷一枚均匀的硬币并记录抛掷所得向上面的结果，对特定的 N 次试验，结果正面向上的次数 n N 服从标准二项分布（Binomial Distribution）且

N 次试验中每次试验结果相互独立，可定义一系列独立的随机变量（Random Variable） X k (k = 1,2,…) ，并且当抛掷结果为正面时 X k = 1 否则为 -1 ，因此 X k = ±1 且取何值具有相同的概率。对随机变量 X k (k = 1,2,…,N) 求和可得

且由 m−(N−m) = k 变换得 m = N+k / 2 ，因此

可以证明 ，

并且 E (| W N |) 渐近于 √ 2N/ π ，因此当 N 充分大时可根据以下公式算出 π 的近似值

这些蒙特卡罗方法对 π 的估计值相较于其他方法均以较慢的速度渐近于 π ，而且不能提供关于已经估算到 π 的小数点后多少位的相关信息，因此当追求速度或精度时，这些方法难以用于估计 π 。

动态系统／遍历理论

物理学

Δ Δ --> x Δ Δ --> p ≥ ≥ --> h 4 π π --> {\displaystyle \Delta x\Delta p\geq {\frac {h}{4\pi }}} (海森堡不确定性原理)

R i k − − --> g i k R 2 + Λ Λ --> g i k = 8 π π --> G c 4 T i k {\displaystyle R_{ik}-{g_{ik}R \over 2}+\Lambda g_{ik}={8\pi G \over c^{4}}T_{ik}} (相对论的场方程)

统计学

高精度π的应用

一般工程或天文运算不需要成千上万位精确度的π，因为四十位精确度的π在计算银河系大小的圆周时，其误差已经小于一个质子。现今精度高π应用于计算机软硬件的测试，以不同的算法计算π而结果误差大代表计算机系统可能出问题。

尚待解决的问题

关于π未解决的问题包括：

它是否是一个正规数，即π的十进制运算式是否包含所有的有限数列。对于二进制运算式，在2000年Bailey及Crandall借助贝利-波尔温-普劳夫公式，证明了π的2-正规性可以由一个有关混沌理论的合理但尚未证明的猜想导出。

0, ..., 9 是否以完全随机的形态出现在π的十进制运算式中。若然，则对于非十进制运算式，亦应有类似特质。

究竟是否所有 0, ..., 9 都会无穷地在π的小数运算式现。

π π --> 2 {\displaystyle \pi ^{\sqrt {2}}} 、 ln ⁡ ⁡ --> π π --> {\displaystyle \ln \pi } 、 π π --> + e {\displaystyle \pi +e} 等（e {\display数学常数e e}为另一个数学常数和无理数）是否为无理数。

采用π为符号

欧拉普及使用希腊字母π作为圆周率。

现时所知，最早使用希腊字母π代表圆周率，是威尔士数学家威廉·琼斯的1706年著作《Synopsis Palmariorum Matheseos; or, a New Introduction to the Mathematics》。 书中首次出现希腊字母π，是讨论半径为1的圆时，在短语“1/2 Periphery (π)”之中。 他选用π，或许由于π是periphery（周边）的希腊语对应单词 περιφέρεια 的首字母。

然而，其他数学家未立刻跟从，有时数学家会用 c , p 等字母代表圆周率。 将π的这个用法推广出去的，是数学家欧拉。他在1736年的著作《Mechanica》开始使用π。因为欧拉与欧洲其他数学家通信频繁，这样就把π的用法迅速传播。 1748年，欧拉在广受阅读的名著《无穷小分析引论》（Introductio in analysin infinitorum）使用π。他写道：“为简便故，我们将这数记为π，因此π=半径为1的圆的半周长，换言之π是180度弧的长度。”于是π就在西方世界得到普遍接受。

评论

近年来，有部分学者认为约等于3.14的π“不合自然”，应该用双倍于π、约等于6.28的一个常数代替。支持这一说法的学者认为在很多数学公式2π很常见，很少单独使用一个π。美国哈佛大学物理学教授的迈克尔·哈特尔称“圆形与直径无关，而与半径相关，圆形由离中心一定距离即半径的一系列点构成”，并建议使用希腊字母τ来代替π 。

美国数学家鲍勃·帕莱（Bob Palais）于2001年在《数学情报》（The Mathematical Intelligencer）上发表了一篇题为《π 是错误的！》（π Is Wrong!）的论文。在论文的第一段，鲍勃·帕莱说道：

美国数学家麦克·哈特尔（Michael Hartl） 建立了网站 tauday.com ，呼吁人们用希腊字母 τ（发音：tau）来表示“正确的”圆周率 C/r。并建议大家以后在写论文时，用一句“为方便起见，定义 τ = 2π ”开头。

著名的 Geek 漫画网站 spikedmath.com 建立了 thepimanifesto.com，里面有一篇数千字的 π 宣言，反驳支持τ的言论，宣称圆周率定义为圆周与直径之比有优越性，并认为在衡量圆柱形物体的截面大小时，直径比半径更方便测量。

文化

背诵

圆周率背诵世界记录的趋势

世界记录是100,000位，由日本人原口证于2006年10月3日背诵。

普通话用谐音记忆的有“山巅一寺一壶酒，尔乐苦煞吾，把酒吃，酒杀尔，杀不死，乐而乐”，就是3.1415926535897932384626。 另一谐音为：“山巅一石一壶酒，二妞舞扇舞，把酒沏酒搧又搧，饱死啰”，就是3.14159265358979323846。

在英文，会使用英文字母的长度作为数字，例如“How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of the geometry, Herr Planck, is fairly hard, and if the lectures were boring or tiring, then any odd thinking was on quartic equations again.”就是3.1415926535897932384626433832795。

数学外的用途

在Google公司2005年的一次公开募股中，集资额不是通常的整头数，而是$14,159,265，这当然是由π小数点后的位数得来。（顺便一提，谷歌公司2004年的首次公开募股，集资额为$2,718,281,828，与数学常数 e 有关）

排版软件TeX从第三版之后的版本号为逐次增加一位小数，使之越来越接近π的值：3.1，3.14，……当前的最新版本号是3.14159265

3月14日为美国所订的圆周率日。

注释

Arndt, Jörg; Haenel, Christoph.Pi Unleashed. Springer-Verlag. 2006 [ 2013-06-05 ] . ISBN 978-3-540-66572-4. English translation by Catriona and David Lischka.

相关条目

含π的公式列表

刘徽割圆术

密率

证明22/7大于π

无理数

欧拉数

e

314

圆周率日

费曼点

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。