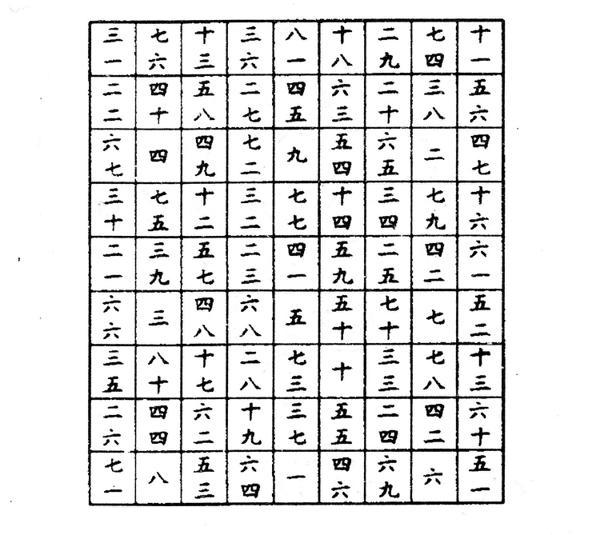
杨辉算法
田亩比类乘除捷法
《田亩比类乘除捷法》二卷。卷上叙述长田形、圭田、斜田、圆田、环田、苑田和丘田的面积计算以及圭垛、梯形垛、方箭、圆箭等数列求和。
乘除通变算宝
《乘除通变算宝》三卷。
卷上《算法通变本末》
《习算纲目》,杨辉为学员制定的学习纲目和时间表,例如 “学相乘起例定位 功课一日”,“温习九归题目 一日”;“开方乃算法中大节目”,用两月演习题目等。
商用乘除算题;此卷详细叙述六种乘法和五种速算加法 。
六种速算乘法
五种速算加法
加一位法,用于乘法 11 至 19 例:274 * 16 = 274 * 10 + 274 *6, 即 将274 *6 + 274 左移一位 ( = * 10)
加二位法,用于乘数 111 至 119,例:274 * 116 = 274 左翼二位 + 274 左移一位 + 275 *6 = 27400 +2740 +274*6
加隔位法,用于乘数101 至 109
重加
连身加,用于乘数 21-29
五种速算减法
减一位
减二位
重减
隔为减
卷中《乘除通变算宝》
叙述乘除通变算宝,和筹算速算法,包括加法乘、九归新括。
卷下《法算取用本末》
是前两卷所述各种方法的应用题例,1-300筹算速算法。用代数方法建立二至四次方程从已知面积求线段,
续古摘奇算法
《续古摘奇算法》二卷。
卷上叙述纵横图、幻方、幻圆;求年内日甲,地支逢宿、甲子逢宿;数列求和,量仓法,面积速算等。
纵横图:洛书,河图,四四图,五五图,六六图,六十四图,九九图,百子图,聚五图,聚六图,聚八图,攒九图,八阵图,连环图。

杨辉九九图

杨辉百子图

杨辉八阵图
杨辉攒九图

杨辉连环图
三五七数二问,七八九数,十一十二十三,三五七九,六十甲子纳音,求年内日甲子积数,地支逢宿,甲子逢宿,量仓法,共卖纱绢等。
卷下叙述二次方程求解,鸡兔同笼,百鸡问题;乘除速算,盈不足,方圆论和海岛问题等19问。
三鸡折直,三果共价,方金求重,开河问积,河上荡杯,引绳量木,贼人盗绢盈不足,方圆总论,隔水望木(海岛)等。
版本
宋刊杨辉算法(失)
明代洪武古杭勤德堂木刻本。
明《永乐大典》
1433年朝鲜刊《杨辉算法》。北京图书馆藏。
清乾隆丙申年(1776年)知不足斋丛书第二十七集《续古摘奇算法》卷下。
清道光郁松年刻《杨辉算法》六卷。
1661年日本关孝和传写《杨辉算法》足本三册。
1917年日本三上义夫将关孝和抄足本《杨辉算法》抄寄李俨,现藏中国科学院自然科学史研究所。
《算法通变本末》《乘除通变算宝》《法算取用本末》商务印书馆 丛书集成 #1192一九三六年
《田亩比类乘除捷法》 《续古摘奇算法》 中华书局 1985(不全,缺幻方幻圆内容)
《杨辉算法》 孙宏安 译注 辽宁教育出版社 1997
《杨辉算法导读》 郭熙汉 湖北教育出版社 1996
参考文献
来源
吴文俊主编:《中国数学史大系》第五卷 556-569
蓝丽蓉:The Yang Hui Suan Fa, a Thirteen Century Chinese Mathematical Treatise, 香港《崇基学报》 1968.
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

相关资料

- 有价值
- 一般般
- 没价值








推荐阅读


关于我们

APP下载