典型盈亏问题

证明

刘徽在为《九章算术》作注时，利用齐同原理对盈不足术进行了证明：“盈朒维乘两设者，欲为同齐之意。……齐其假令，同其盈朒……通计齐则不盈不朒之正数，故可并之为实，并盈、不足为法。”

刘徽指出，交叉相乘的意义是使其“同齐”。每人所出为 a 1 {\displaystyle a_{1}} 时，盈 b 1 {\displaystyle b_{1}} ，那么总价变为 b 2 {\displaystyle b_{2}} 倍、每人所出变为 a 1 b 2 {\displaystyle a_{1}b_{2}} 时，盈 b 1 b 2 {\displaystyle b_{1}b_{2}} 。每人所出为 a 2 {\displaystyle a_{2}} 时，不足 b 2 {\displaystyle b_{2}} ，那么总价变为 b 1 {\displaystyle b_{1}} 倍、每人所出变为 a 2 b 1 {\displaystyle a_{2}b_{1}} 时，不足 b 1 b 2 {\displaystyle b_{1}b_{2}} 。这样就“同其盈朒”，两者相加则盈亏相抵，就“不盈不朒”，此时总价为 b 1 + b 2 {\displaystyle b_{1}+b_{2}} 倍，每人所出为 a 1 b 2 + a 2 b 1 {\displaystyle a_{1}b_{2}+a_{2}b_{1}} ，相除即得到总价不变时每人所出的钱。

双假设法

除盈亏类问题，《九章算术》还通过双假设法，将其他算术问题转化、套入盈亏类问题的算法模型，进行求解。如：

该问题本属于鸡兔同笼，而通过两次假设可以将其转化为盈亏类问题，再用盈不足术求解。

非线性问题

盈不足术实际上是一种线性插值法；对于非线性的问题，所求出的只是其近似值。《九章算术》和刘徽都没有意识到这一点。 如：

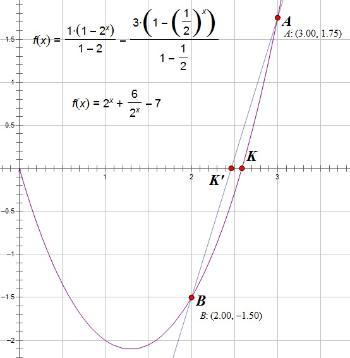
  点K为函数f(x)的根。点A、B为通过假设得出的盈、不足的情况，过两点作直线，直线的根即近似值K"。

实际上该问题是非线性的。根据等比数列求和公式，可以将莞草与蒲草的长度差表示为：

f ( x ) = 1 ∗ ∗ --> ( 1 − − --> 2 x ) 1 − − --> 2 − − --> 3 ∗ ∗ --> ( 1 − − --> 0.5 x ) 1 − − --> 0.5 = 2 x + 6 2 x − − --> 7 {\displaystyle f(x)={\frac {1*(1-2^{x})}{1-2}}-{\frac {3*(1-0.5^{x})}{1-0.5}}=2^{x}+{\frac {6}{2^{x}}}-7}

所求即为 f ( x ) {\displaystyle f(x)} 的正数根。解得 x = log 2 ⁡ ⁡ --> 6 = 1 + lg ⁡ ⁡ --> 3 lg ⁡ ⁡ --> 2 {\displaystyle x=\log _{2}6=1+{\frac {\lg 3}{\lg 2}}} 。

而使用盈不足术所求出的答案实为近似值。两者关系见右图。

这种利用双假设法加盈不足术来求解一些复杂方程的根的近似值的方法，在现在的高等数学中被应用于线性插值近似法和弦截法。

历史

在中国最早的数学书《算数书》中，就有通过盈不足术计算面积为一亩的正方形田地的边长的记载。 《九章算术》第七章“盈不足”，则是对双假设法最早的详细说明。

黄金时代的阿拉伯数学家也大量研究了双假设法。 阿布·卡米勒 （ 英语 ： Abū_Kāmil_Shujāʿ_ibn_Aslam ） 著有《双假设法之书》（ Kitāb al-khaṭaʾayn ）。 古斯塔·伊本·卢卡 （ 英语 ： Qusta ibn Luqa ） 采用欧式几何的方法，第一次对双假设法给出了几何证明。

中世纪欧洲数学家斐波那契在《 计算之书 （ 英语 ： Liber Abaci ） 》的第十三章中讨论了双假设法。他明确承认该方法来自阿拉伯数学，并称之为 elchataym ，即来自阿拉伯语的 al-khaṭāʾayn 。 在代数符号尚未普及的时代，这种万能算法在欧洲流传甚广，兴盛一时。

明朝时，中国传统数学已经衰落，《九章算术》近乎失传，盈不足术不为人所知。利玛窦和李之藻将克里斯托弗·克拉维乌斯的《实用算术概论》（ Epitome arithmeticae practicae ）编译为《同文算指》，将其中的双假设法称为“叠借互征法”。

钱宝琮最早提出，阿拉伯数学中的双假设法来自中国的盈不足术， al-khaṭāʾayn 即与“契丹”有关。 李约瑟也认为有此种可能性。 这种说法已被中国数学史界广泛接受；但也有学者认为，中国盈不足术是欧洲双假设法的源头的说法仍然缺乏令人信服的证据支持。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。