定义

假设G{\displaystyle G}，是群而S{\displaystyle S}，是生成集。凯莱图Γ Γ -->=Γ Γ -->(G,S){\displaystyle \Gamma =\Gamma (G,S)}，是如下构造的着色的有向图。

G{\displaystyle G}，每个元素g{\displaystyle g}，指派一个顶点：Γ Γ -->{\displaystyle \Gamma }，的顶点集合V(Γ Γ -->){\displaystyle V(\Gamma )}，同一于G{\displaystyle G}，。

S{\displaystyle S}，的每个生成元s{\displaystyle s}，指派一种颜色cs{\displaystyle c_{s}}，。

对于任何g∈ ∈ -->G,s∈ ∈ -->S{\displaystyle g\in G,s\in S}，对应于元素g{\displaystyle g}，和gs{\displaystyle gs}，的顶点用颜色cs{\displaystyle c_{s}}，的有向边连接。因此边集合E(Γ Γ -->){\displaystyle E(\Gamma )}，由形如(g,gs){\displaystyle (g,gs)}，的有序对构成，带着s∈ ∈ -->S{\displaystyle s\in S}提供的颜色。

在几何群论中，集合S{\displaystyle S}，通常被假定为有限的、“对称的”也就是S=S− − -->1{\displaystyle S=S^{-1}}，并且不包含这个群的单位元。在这种情况下，凯莱图是正常的图：它的边没有方向并且不包含环路。

例子

假设G = Z是无限循环群而集合S有标准生成元1和它的逆元（用加法符号为−1）构成，则它的凯莱图是无穷链。

类似的，如果G = Zn是n阶循环群而S由两个元素构成，G的标准生成元和它的逆元，则凯莱图是环图Cn。

群的直积的凯莱图是对应的凯莱图的笛卡尔积。因此带有四个元素（±1, ±1）组成的生成集的阿贝尔群Z的凯莱图是在平面R上无穷网格，而带有类似的生成集的直积Zn×Zm的凯莱图是在环面上n乘m有限网格。

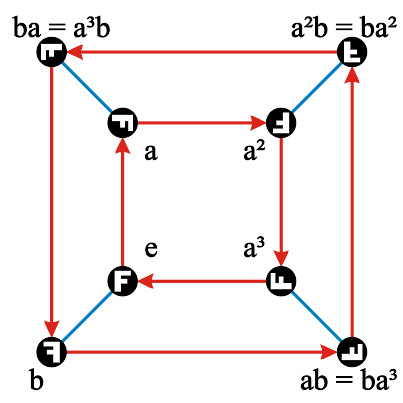
二面体群D4在两个生成元a和b上的凯莱图。

二面体群D4在两个生成元a和b上的凯莱图列于右侧。红色箭头表示左乘元素a。因此元素b是自我逆转的，表示左乘元素b蓝色线是无方向的。因此这个图是混合的：它有8个顶点，8个有向边，4个边。群D4的凯莱表可以从群展示得出：

在对应于集合S = {a, b, a, b}的两个生成元a, b上的自由群的凯莱图列出在文章开头，这里的e表示单位元。沿着边向右走表示右乘a，而沿着变向上走表示乘以b。因为自由群没有关系，它的凯莱图中没有环。这个凯莱图是证明巴拿赫-塔斯基悖论的关键因素。

特征

群G{\displaystyle G}通过左乘作用在自身上（参见凯莱定理）。这个作用可以看作G{\displaystyle G}作用在它的凯莱图上。明显的，一个元素h∈ ∈ -->G{\displaystyle h\in G}映射一个顶点g∈ ∈ -->V(Γ Γ -->){\displaystyle g\in V(\Gamma )}到顶点hg∈ ∈ -->V(Γ Γ -->){\displaystyle hg\in V(\Gamma )}。凯莱图的边集合被这个作用所保存：边(g,gs){\displaystyle (g,gs)}变换成边(hg,hgs){\displaystyle (hg,hgs)}。任何群在自身上的左乘作用是简单传递的，特别是凯莱图是顶点传递的。这导致了凯莱图的下列特征：

要从一个凯莱图Γ Γ -->=Γ Γ -->(G,S){\displaystyle \Gamma =\Gamma (G,S)}恢复群G{\displaystyle G}和生成集S{\displaystyle S}，选择一个顶点v1∈ ∈ -->V(Γ Γ -->){\displaystyle v_{1}\in V(\Gamma )}并标记上这个群的单位元。接着对每个Γ Γ -->{\displaystyle \Gamma }的顶点v{\displaystyle v}标记上变换v1{\displaystyle v_{1}}到v{\displaystyle v}的G{\displaystyle G}的唯一元素。产生Γ Γ -->{\displaystyle \Gamma }为凯莱图的G{\displaystyle G}的生成元的集合S{\displaystyle S}是毗连到选择的顶点的顶点的标记的集合。生成集合是有限（这是凯莱图的共同假定）当且仅当这个图是局部有限的（就是说每个顶点毗连与有限多个边）。

基本性质

如果生成集合的成员s{\displaystyle s}是自身的逆元，即s=s− − -->1{\displaystyle s=s^{-1}}，则它一般被表示为无向边。

凯莱图Γ Γ -->(G,S){\displaystyle \Gamma (G,S)}本质上依赖于生成元的集合S{\displaystyle S}的选择方式。例如，如果生成集合S{\displaystyle S}有k{\displaystyle k}个元素，则凯莱图的每个顶点都有k{\displaystyle k}个进入和k{\displaystyle k}个外出的有向边。在有r{\displaystyle r}个元素的对称生成集合S{\displaystyle S}的情况下，凯莱图是r{\displaystyle r}度的正则图。

在凯莱图中的环（“闭合路径”）指示在S{\displaystyle S}的两个元素之间的关系。在群的凯莱复形的更精细构造中，对应于关系的闭合路径被用多边形“填充”。

如果f:G′→ → -->G{\displaystyle f:G"\to G}是满射群同态并且G′{\displaystyle G"}的生成集合S′{\displaystyle S"}的元素的像是不同的，则它引发一个图的覆盖

图Γ Γ -->(G,S){\displaystyle \Gamma (G,S)}可以被构造即使集合S{\displaystyle S}不生成群G{\displaystyle G}。但是，它是连通的并不被认为是凯莱图。在这种情况下，这个图的每个连通部件表示一个S{\displaystyle S}生成子群的陪集。

对于被认为是无向的凯莱图，顶点连通性等于这个图的度。

Schreier陪集图

如果转而把顶点作为固定子群H{\displaystyle H}的右陪集，就得到了一个有关的构造Schreier陪集图，它是陪集枚举或Todd-Coxeter算法的基础。

与群论的关系

研究图的邻接矩阵特别是应用谱图理论的定理能洞察群的结构。

参见

群的生成集合

群的展示

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。