



CAP定理
历史这个定理起源于柏克莱加州大学(UniversityofCalifornia,Berkeley)的计算机科学家埃里克·布鲁尔在2000年的分布式计算原则研讨会(SymposiumonPrinciplesofDistributedComputing(英语:SymposiumonPrinciplesofDistributedComputing)(PODC))上提出的一个猜想。在2002年,麻省理工学院(MIT)的赛斯·吉尔伯特(英语:SethGilbert)和南希·林奇(英语:NancyLynch)发表了布鲁尔猜想的证明,使之成为一个定理。吉尔伯特和林奇证明的CAP定理比布鲁尔设想的某种程度上更加狭义。定理讨论了在两个互相矛盾的请求到达彼此连接不通的两个不同的分布式节点的时候的处理方案。参见分布式计算的谬论(FallaciesofDistributedComputing(英语:Fallaci...
历史
这个定理起源于柏克莱加州大学(University of California, Berkeley)的计算机科学家埃里克·布鲁尔在2000年的分布式计算原则研讨会( Symposium on Principles of Distributed Computing ( 英语 : Symposium on Principles of Distributed Computing ) (PODC))上提出的一个猜想。 在2002年,麻省理工学院(MIT)的 赛斯·吉尔伯特 ( 英语 : Seth Gilbert ) 和 南希·林奇 ( 英语 : Nancy Lynch ) 发表了布鲁尔猜想的证明,使之成为一个定理。
吉尔伯特和林奇证明的CAP定理比布鲁尔设想的某种程度上更加狭义。定理讨论了在两个互相矛盾的请求到达彼此连接不通的两个不同的分布式节点的时候的处理方案。
参见
分布式计算的谬论( Fallacies of Distributed Computing ( 英语 : Fallacies of Distributed Computing ) )
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 定理
各种数学叙述(按重要性来排列)引理(又称辅助定理,补理)-某个定理的证明的一部分的叙述。它并非主要的结果。引理的证明有时还比定理长,例如舒尔引理。推论-一个从定理随之而即时出现的叙述。若命题B可以很快、简单地推导出命题A,命题A为命题B的推论。命题定理数学原理结构定理一般都有许多条件。然后有结论——一个在条件下成立的数学叙述。通常写作“若条件,则结论”。用符号逻辑来写就是条件→结论。而当中的证明不视为定理的成分。逆定理若存在某叙述为A→B,其逆叙述就是B→A。逆叙述成立的情况是A←→B,否则通常都是倒果为因,不合常理。若果叙述是定理,其成立的逆叙述就是逆定理。若某叙述和其逆叙述都为真,条件必要且充足。若某叙述为真,其逆叙述为假,条件充足。若某叙述为假,其逆叙述为真,条件必要。逻辑中的定理命题集合的可计算性问题(Calculabilite)我们可以通过可计算性(Calculabilite)这...
· 采样定理
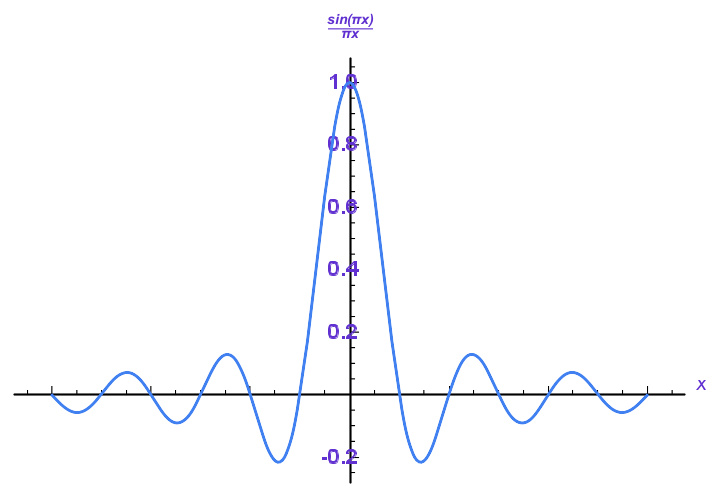
简介采样是将一个信号(例如时间或空间上连续的函数)转换为数字序列(时间或空间上离散的函数)的过程。这个定理的香农版本陈述为:如果函数x(t)不包含高于Bcps(次/秒)的频率,它完全取决于一系列相隔1/(2B)秒的点的纵坐标。因此2B样本/秒或更高的采样频率就足够了。相反,对于一个给定的采样频率fs,完全重构的频带限制为B≤fs/2。在频带限制过高(或根本没有频带限制)的情形下,重构表现出的缺陷称为混叠。现在对于此定义的陈述有时会很小心的指出x(t)必须不包括频率恰好为B的正弦曲线,或是B必须小于½的采样频率。这二个门槛,2B及fs/2会称为奈奎斯特速率(英语:Nyquistrate)及奈奎斯特频率。这些是x(t)及采样设备的属性。上述的不等式会称为奈奎斯特准则,有时会称为拉贝准则(Raabecondition)。此定理也可以用在其他定义域(例如离散系统)的函数下,唯一的不同是量测t,fs...
· 罗尔定理
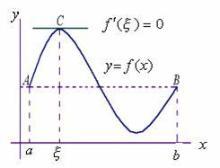
证明罗尔定理的几何意义首先,因为f{\displaystylef}在闭区间[a,b]{\displaystyle[a,b]}上连续,根据极值定理,f{\displaystylef}在[a,b]{\displaystyle[a,b]}上有最大值和最小值。如果最大值和最小值都在端点a{\displaystylea}或b{\displaystyleb}处取得,由于f(a)=f(b){\displaystylef(a)=f(b)},f{\displaystylef}显然是一个常数函数。那么对于任一点ξξ-->∈∈-->(a,b){\displaystyle\xi\in(a,b)},我们都有f′′-->(ξξ-->)=0{\displaystylef^{\prime}(\xi)=0}。现在假设f{\displaystylef}在ξξ-->∈∈-->(a,b){\d...
· 卢津定理
定理叙述一维形式设f:[a,b]→→-->C{\displaystylef:[a,b]\to\mathbb{C}}是可测函数,对任何ϵϵ-->>0{\displaystyle\epsilon>0},都存在紧致集E⊂⊂-->[a,b]{\displaystyleE\subset[a,b]},使得λλ-->([a,b]∖∖-->E){\displaystyle\lambda([a,b]\setminusE),而且f限制到E上是连续函数。此处λλ-勒贝格测度{\displaystyle\lambda}是勒贝格测度。证明因为f可测,所以在一个测度任意小的开集以外,f是有界函数。在开集上重定义f为0,那么f在[a,b]上有界,因而是可积函数。因为连续函数在可积函数的空间L1([a,b]){\displaystyle\mathrm{L}^{1}([a,b])}...
· 介值定理
定理假设I=[a,b]{\displaystyleI=[a,b]}是一个实数里的闭区间,而f::-->I→→-->R{\displaystylef\colonI\rightarrow\mathbb{R连续函数是连续函数,那么其像集f(I){\displaystylef(I)}也是区间。它或者包含[f(a),f(b)]{\displaystyle[f(a),f(b)]}(如果f(a)≤≤-->f(b){\displaystylef(a)\leqf(b)}),或者包含[f(b),f(a)]{\displaystyle[f(b),f(a)]}(如果f(b)≤≤-->f(a){\displaystylef(b)\leqf(a)})。换言之:f(I)⊇⊇-->[f(a),f(b)]{\displaystyle\displaystylef(I)\supseteq[f(a)...
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信
















