定义

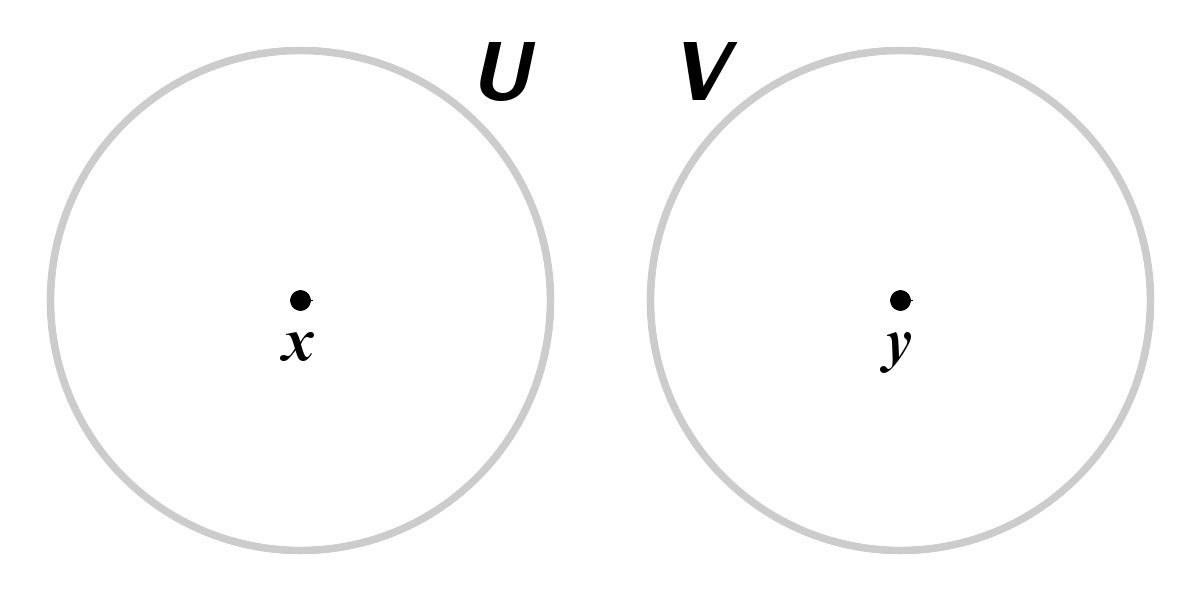
两个点x和y，由它们各自的邻域U和V来分离。

假设 X 是拓扑空间。设 x 和 y 是 X 中的点。我们称 x 和 y 可以“由邻域分离”，如果存在 x 的邻域 U 和 y 的邻域 V 使得 U 和 V 是不相交的（ U ∩ V = ∅），且 X 中的任意两个不同的点都可以由这样的邻域分离，那么称 X 是 豪斯多夫空间 。这也是豪斯多夫空间叫做 T 2 空间 或 分离空间 的原因。

X 是 预正则空间 ，如果任何两个拓扑可区分的点可以由邻域分离。预正则空间也叫做 R 1 空间 。

在这些条件之间的联系如下。拓扑空间是豪斯多夫空间，当且仅当它是预正则空间和柯尔莫果洛夫空间的二者（就是说独特的点是拓扑可区分的）。拓扑空间是预正则空间，当且仅当它的柯尔莫果洛夫商空间是豪斯多夫空间。

等价

对于拓扑空间 X ，以下论述等价：

X {\displaystyle X} 是豪斯多夫空间。

{ ( x , x ) | x ∈ ∈ --> X } {\displaystyle \{(x,x)|x\in X\}} 是积空间 X × × --> X {\displaystyle X\times X} 的闭集。

X 中极限是唯一的(就是序列、网和滤子收敛于最多一个点)。

所有包含在 X 中的单元素集合都等于包含它的所有闭邻域的交集。

例子和反例

在数学分析所遇到的几乎所有空间都是豪斯多夫空间；最重要的实数是豪斯多夫空间。更一般的说，所有度量空间都是豪斯多夫空间。事实上，在分析中用到的很多空间，比如拓扑群和拓扑流形在其定义中明确的声明了豪斯多夫条件。

最简单的是T 1 空间而非T 2 空间的拓扑的例子是余有限空间。

伪度量空间典型的不是豪斯多夫空间，但是它们是预正则的，并且它们在分析中通常只用于构造豪斯多夫gauge空间。实际上，在分析家处理非豪斯多夫空间的时候，它至少要是预正则的，他们简单的把它替代为是豪斯多夫空间的它的柯尔莫果洛夫商空间。

相反的，在抽象代数和代数几何更经常见到非预正则空间，特别是作为在代数簇或交换环谱上的扎里斯基拓扑。他们还出现在直觉逻辑的模型论中：所有完全Heyting代数都是某个拓扑空间的开集的代数，但是这个空间不需要是预正则的，更少见豪斯多夫空间。

性质

豪斯多夫空间的子空间和乘积是豪斯多夫空间， 但是豪斯多夫空间的商空间不必须是豪斯多夫空间。事实上，所有拓扑空间都可以实现为某个豪斯多夫空间的商。

豪斯多夫空间是T 1 空间，这意味着所有单元素集合是闭集。类似的，预正则空间是R 0 空间。

豪斯多夫空间另一个美好的性质是紧致集合总是闭集。 这对于非豪斯多夫空间就可能失效（例如有其失效的T 1 空间的例子）。

豪斯多夫空间的定义声称点可以由邻域分离。它蕴涵了表象上更强的东西：在豪斯多夫空间中所有成对的不相交的紧致集合都可以由邻域分离。 这是紧致集合经常表现得如同点的一般规则的一个例子。

紧致性条件与预正则一起经常蕴涵了更强的分离公理。例如，任何局部紧致预正则空间都是完全正则空间。紧致预正则空间是正规空间，意味着它们满足乌雷松引理和蒂茨扩张定理，并且有服从局部有限开覆盖的单位划分。这些陈述的豪斯多夫版本是：所有局部紧致豪斯多夫空间是吉洪诺夫空间，而所有紧致豪斯多夫空间是正规豪斯多夫空间。

下列结果是关于来或到豪斯多夫空间的映射(连续函数和其他)的技术上的性质。

设 f : X → Y 是连续函数并假定 Y 是豪斯多夫空间。则 f 的图象 { ( x , f ( x ) ) : x ∈ ∈ --> X } {\displaystyle \{(x,f(x)):x\in X\}} 是 X × Y 的闭子集。

设 f : X → Y 是函数并设 ker ( f ) = { ( x , x ′ ) : f ( x ) = f ( x ′ ) } {\displaystyle {\mbox{ker}}(f)=\{(x,x"):f(x)=f(x")\}} 是作为 X × X 的子空间的它的核。

如果 f 是连续函数并且 Y 是豪斯多夫空间则ker( f )闭集。

如果 f 是开满射而ker( f )是闭集则 Y 豪斯多夫空间。

如果 f 是连续开满射（就是开商映射），则 Y 是豪斯多夫空间，当且仅当ker(f)是闭集。

如果 f,g : X → Y 是连续映射而 Y 是豪斯多夫空间，则均衡子 eq ( f , g ) = { x : f ( x ) = g ( x ) } {\displaystyle {\mbox{eq}}(f,g)=\{x:f(x)=g(x)\}} 在 X 是闭集。可得出如果 Y 是豪斯多夫空间而 f 和 g 一致于 X 的稠密子集，则 f = g 。换句话说，到豪斯多夫空间的连续函数确定自它们在稠密子集上的值。

设 f : X → Y 是闭满射使得 f ( y )对于所有 y ∈ Y 是紧致的。则如果 X 是豪斯多夫空间则 Y 也是。

设 f : X → Y 是商映射带有 X 是紧致豪斯多夫空间。则下列是等价的

Y 是豪斯多夫空间

f 是闭映射

ker( f )是闭集

预正则性和正则性

所有正则空间都是预正则空间，也都是豪斯多夫空间。有很多拓扑空间的结果对正则空间和豪斯多夫空间二者都成立。多数时候这些结果对于所有预正则空间也成立；它们对正则空间和豪斯多夫空间要分开列出，因为预正则空间的概念要更晚。在另一方面，这些对于正则性为真的结果一般不适用于非正则豪斯多夫空间。

有很多情况拓扑空间的其他条件（比如仿紧致性或局部紧致性）也蕴涵正则性，如果它满足预正则性的话。这种条件经常有两个版本：正则版本和豪斯多夫版本。尽管豪斯多夫空间一般不是正则性的，局部紧致的豪斯多夫空间是正则性的，因为任何豪斯多夫空间都是预正则性的。因此从特定角度来看，在有关这些情况的时候它实际是预正则性的，而非正则性的。但是，定义仍依据正则性来措辞，因为这些条件比预正则性更周知。

更详细细节请参见分离公理的历史。

变体

术语“豪斯多夫”、“分离”和“预正则”还可以用于在拓扑空间上的变体如一致空间、柯西空间和收敛空间。在所有这些例子中统一的概念特征是网或滤子（在它们存在的时候）的极限是唯一的（对于分离空间）或在拓扑同构意义下唯一的（对于预正则空间）。

这显现出一致空间和更一般的柯西空间总是预正则的，所有在这些情况下豪斯多夫条件简约为T 0 条件。还有完备性在其中有意义的空间，豪斯多夫性在这些情况下是完备性的自然伙伴。特别是，一个空间是完备的，当且仅当所有柯西网有至少一个极限，而一个空间是豪斯多夫的，当且仅当所有柯西网都有最多一个极限（因为只有柯西网可以首先有极限）。

引用

Munkres, J. R., 2000, Topology , 2nd edition, Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-181629-9

赵文敏，《拓扑学导论》，九章出版社，ISBN 978-957-603-018-5

Arkhangelskii, A.V., L.S.Pontryagin, General Topology I ,（1990）Springer-Verlag, Berlin. ISBN 978-3-540-18178-1

Bourbaki; Elements of Mathematics: General Topology , Addison-Wesley (1966).

Willard, Stephen. General Topology. Dover Publications. 2004. ISBN 978-0-486-43479-7.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。