历史

在1882年，Walther Dyck 在发表于 Mathematische Annalen 的论文 Gruppentheoretische Studien 中研究了自由群的概念，但未加以命名。“自由群”一词由 Jakob Nielsen 于1924年引入。

例子

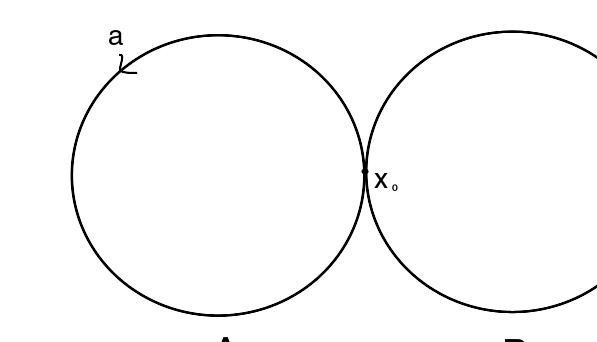
2个圆环的集丛

整数的加法群 ( Z , + ) {\displaystyle (\mathbb {Z} ,+)} 是自由群；事实上我们可取 S := { 1 } {\displaystyle S:=\{1\}} 。

在巴拿赫-塔斯基悖论的论证中用到两个生成元的自由群，以下将予说明。

在代数拓扑学中， k {\displaystyle k} 个圆环的集丛（即： k {\displaystyle k} 个只交于一点的圆环，见右图）的基本群是 k {\displaystyle k} 个生成元的自由群。

建构方式

今将构造集合 S {\displaystyle S} 上之自由群 F ( S ) {\displaystyle F(S)} ，分解动作如下。

对任何 s ∈ ∈ --> S {\displaystyle s\in S} ，引入符号 s − − --> 1 {\displaystyle s^{-1}} ，称作 s {\displaystyle s} 的逆元。

考虑所有由符号 s , s − − --> 1 ( s ∈ ∈ --> S ) {\displaystyle s,s^{-1}\;(s\in S)} 构成的有限字串。

如果一个字串能透过将 s s − − --> 1 {\displaystyle ss^{-1}} 或 s − − --> 1 s {\displaystyle s^{-1}s} 替换为空字串而变为另一个字串，则称这两个字串等价；此关系在所有上述字串构成的等价关系成一等价关系，其商集（等价类构成的集合）记作 F ( S ) {\displaystyle F(S)} 。

我们可以借着对字串长度作数学归纳法，证明此等价关系相容于字串的接合，即： x ∼ ∼ --> y , x ′ ∼ ∼ --> y ′ ⇒ ⇒ --> x x ′ ∼ ∼ --> y y ′ {\displaystyle x\sim y,x"\sim y"\Rightarrow xx"\sim yy"} 。故字串接合在 F ( S ) {\displaystyle F(S)} 导出二元运算，并满换律。

取 F ( S ) {\displaystyle F(S)} 及字串接合运算构成一个群，字串 s 1 ± ± --> 1 ⋯ ⋯ --> s n ± ± --> 1 {\displaystyle s_{1}^{\pm 1}\cdots s_{n}^{\pm 1}} 之逆为 s n ∓ ∓ --> 1 ⋯ ⋯ --> s 1 ∓ ∓ --> 1 {\displaystyle s_{n}^{\mp 1}\cdots s_{1}^{\mp 1}} 。此即所求。

若 S {\displaystyle S} 为空集，则 F ( S ) {\displaystyle F(S)} 为平凡群。

泛性质

上述构造 F ( S ) {\displaystyle F(S)} 带有一个自然的集合映射 ϕ ϕ --> : S → → --> F ( S ) {\displaystyle \phi :S\rightarrow F(S)} 。这对资料 ( F ( S ) , ϕ ϕ --> ) {\displaystyle (F(S),\phi )} 满足以下泛性质：

事实上我们仅须，也必须设 f ( s 1 ± ± --> 1 ⋯ ⋯ --> s n ± ± --> 1 ) := ψ ψ --> ( s 1 ) ± ± --> 1 ⋯ ⋯ --> ψ ψ --> ( p n ) ± ± --> 1 {\displaystyle f(s_{1}^{\pm 1}\cdots s_{n}^{\pm 1}):=\psi (s_{1})^{\pm 1}\cdots \psi (p_{n})^{\pm 1}} ；前述构造确保此式给出一个明确定义的群同态。

任两个满足上述泛性质的资料 ( F 1 , ϕ ϕ --> 1 ) {\displaystyle (F_{1},\phi _{1})} 、 ( F 2 , ϕ ϕ --> 2 ) {\displaystyle (F_{2},\phi _{2})} 同构多差一个同构，因而刻划了自由群的群论性质。这种泛性质是泛代数中考虑的自由对象的特例，用范畴论的语言来说，函子 F ( − − --> ) : S ↦ ↦ --> F ( S ) {\displaystyle F(-):S\mapsto F(S)} 是遗忘函子的左伴随函子。

性质与定理

任何群 G {\displaystyle G} 皆可表为某个自由群的同态像；在上述泛性质中取 S {\displaystyle S} 为 G {\displaystyle G} 的一组生成集，ψ 为包含映射即可。此时 F ( S ) → → --> G {\displaystyle F(S)\rightarrow G} 的核 R {\displaystyle R} 称作 关系 ， F ( S ) , K {\displaystyle F(S),K} 称作 G {\displaystyle G} 的一个 展示 ；若 S {\displaystyle S} 有限，则称之为 有限展示 。一个群可以有多种展示，而且不存在判断两个展示给出的群是否同构的算法。

如果 S {\displaystyle S} 有超过一个元素，则 F ( S ) {\displaystyle F(S)} 非交换；事实上 F ( S ) {\displaystyle F(S)} 的中心只有单位元。

任两个自由群 F ( S ) , F ( T ) {\displaystyle F(S),F(T)} 同构的充要条件是 S , T {\displaystyle S,T} 基数相同，此基数称作自由群的 阶 。

以下是一些相关定理：

Jakob Nielsen 与 Otto Schreirer 的定理：自由群的子群也是自由群。若 G {\displaystyle G} 为 n {\displaystyle n} 阶， ( G : H ) = k {\displaystyle (G:H)=k} ，则 H {\displaystyle H} 为 1 − − --> n + n k {\displaystyle 1-n+nk} 阶（在此设 n , k {\displaystyle n,k} 有限）。

设 F {\displaystyle F} 为超过一阶的自由群；则对任意可数基数 n {\displaystyle n} ， F {\displaystyle F} 中都存在 n {\displaystyle n} 阶的自由子群。

自由群虽然看似是离散的对象，却可藉微分几何或拓扑学工具研究，上述 Nielsen-Schreirer 定理就是一例（可运用同伦上纤维的构造证明）；这套技术属于几何群论的一支。

自由阿贝尔群

更多资料：自由阿贝尔群

将上述泛性质中的“群”替换成“阿贝尔群”，遂得到 自由阿贝尔群 的泛性质。集合 S {\displaystyle S} 上的自由阿贝尔群可视为自由 Z {\displaystyle \mathbb {Z} } -模来构造，或取作 F ( S ) {\displaystyle F(S)} 的“交换化”： F ( S ) / [ F ( S ) , F ( S ) ] {\displaystyle F(S)/[F(S),F(S)]} （换言之，在考虑字串时不计符号顺序）。

塔斯基的问题

塔斯基在1945年左右提出下述问题：

目前已有两个团队独立给出肯定的答案，但双方的证明都尚未被认可。请参见网址[1]的“O8”。

文献

Kharlampovich, Olga; Myasnikov, Alexei, Elementary theory of free non-abelian groups, J. Algebra, 2006, 302 (2): 451–552, doi:10.1016/j.jalgebra.2006.03.033 ,数学评论2293770

W. Magnus, A. Karrass and D. Solitar, "Combinatorial Group Theory", Dover (1976).

Sela, Z., Diophantine geometry over groups. VI. The elementary theory of a free group., Geom. Funct. Anal. 16, 2006, (3): 707–730,数学评论2238945

J.-P. Serre, Trees , Springer (2003) (English translation of "arbres, amalgames, SL 2 ", 3rd edition, astérisque 46 (1983))

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。