截半二十面体
性质截半二十面体每个顶点都是2个三角形和2个五边形的公共顶点,其顶点图可以用3.5.3.5{displaystyle3{.}5{.}3{.}5}表示,也可以简写为(3.5)2{displaysty
性质
截半二十面体每个顶点都是2个三角形和2个五边形的公共顶点,其顶点图可以用 3 . 5 . 3 . 5 {\displaystyle 3{.}5{.}3{.}5} 表示,也可以简写为 ( 3 . 5 ) 2 {\displaystyle \left(3\,{.}\,5\right)^{2}} 。
截半二十面体每十条棱可以成为一个正十边形,共有六个独立的十边形。而这六个独立的十边形也可以独立地与立体中的三角形或五边形单独构成星形多面体。
体积与表面积
边长为a的截半二十面体的表面积约为 29.3059828 a 2 {\displaystyle 29.3059828a^{2}} 、体积约为 13.8355259 a 3 {\displaystyle 13.8355259a^{3}} ,可由下列算式计算 :
二面角
截半二十面体是一种棱可递的多面体,因此其具有所有二面角相等的性质。截半二十面体的二面角为 :
顶点座标
边长为单位长且几何中心位于原点的截半二十面体,其顶点座标为 :
其中φ是黄金比例,值为 1 + 5 2 {\displaystyle {\frac {1+{\sqrt {5}}}{2}}} 。
作法
将一个正十二面体或正二十面体进行截半变换即可得到一个截半二十面体,因此截半二十面体又称截半十二面体,即截半与对偶截半等价。
正交投影
相关多面体及镶嵌
相关多面体
截半二十面体是正二十面体经过截半变换后的结果,其他也是由正二十面体透过康威变换得到的多面体有:
参见
正十二面体
正二十面体
参考文献
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
文章来源:内容词条
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~



打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 小斜方截半二十面体
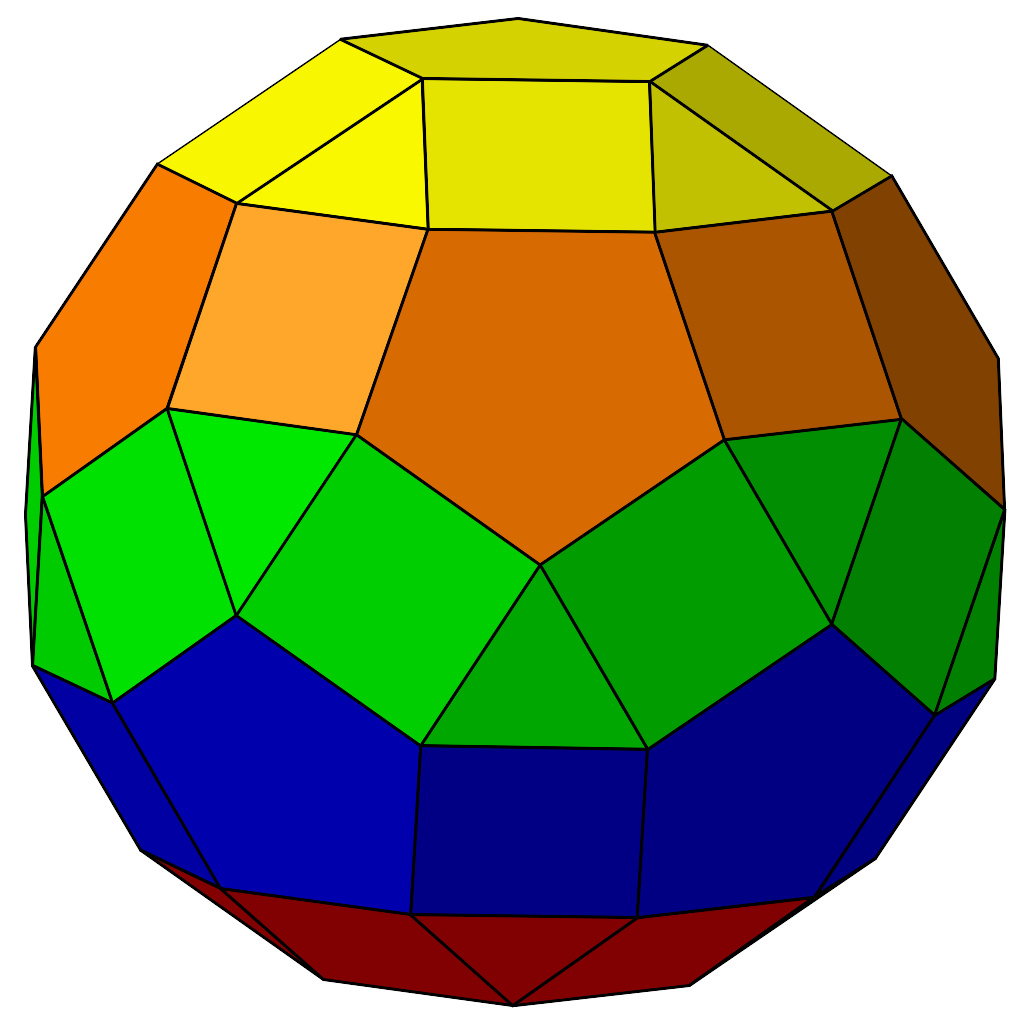
作法将一个正十二面体(正二十面体)三十条棱都切一刀,在二十(十二)个顶点处也切一刀,就可以得到一个小斜方截半二十面体。小斜方截半二十面体的上下分层着色参见正二十面体正十二面体
· 截半立方体
性质截半立方体具有十二个结构相等的顶点,皆为两个三角形与两个正方形的公共顶点、24个结构相等的棱,相邻面皆为三角形与正方形,两面角为反正割负根号三,约125.26度,因此同时具有点可递和边可递的性质,因此是一种均匀多面体、半正多面体和拟正多面体,并且为阿基米德发现的13种半正多面体之一,因此也属于阿基米德立体。此外,由于截半立方体可以视为立方体和其对偶多面体正八面体中三角形与正方形的组合,因此又是一种立方体和其对偶多面体正八面体的立体混合物。截半立方体形成的四个正六边形,以颜色分隔截半立方体是立方体透过截半变换构造而成的多面体,简而言之是用立方体由一条棱斩到另一条棱的中点(即斩去立方体的顶点)而成。因此其正方形面的数目和立方体的面都为6,其三角形面数目和立方体的顶点数目都为8,共有面14个。因为同样种类的正多边形面棱不相交,故可以计算其边数乘以面的数目来得其棱的数目:3×8=4×6=24。...
· 小斜方截半立方体

性质小斜方截半立方体每八条棱可以成为一个正八边形,共可以形成六个独立的正八边形。体积与表面积边长为a{\displaystylea}的小斜方截半立方体,其表面积A{\displaystyleA}和体积V{\displaystyleV}如下:表面积A=(18+23)a2≈≈-->21.4641016a2{\displaystyleA=(18+2{\sqrt{3}})a^{2}\approx21.4641016a^{2}},体积V=13(12+102)a3≈≈-->8.71404521a3{\displaystyleV={\frac{1}{3}}(12+10{\sqrt{2}})a^{3}\approx8.71404521a^{3}}。座标边长为2且几何中心位于原点的小斜方截半立方体,其顶点座标为:的全排列。边长为1的小斜方截半立方体,其对偶多面体鸢形二十四面体的边长为:与其他几何...
· 小斜方截半六边形镶嵌
相关半正镶嵌参考文献Grünbaum,Branko;andShephard,G.C.TilingsandPatterns.NewYork:W.H.Freeman.1987.ISBN0-7167-1193-1.(Chapter2.1:Regularanduniformtilings,p.58-65)Williams,Robert.TheGeometricalFoundationofNaturalStructure:ASourceBookofDesign.DoverPublications,Inc.1979.ISBN0-486-23729-X.p40[1](Chapter21,NamingArchimedeanandCatalanpolyhedraandtilings.MathWorld上Uniformtessellation的资料,作者:埃里克·韦斯坦因。MathWo...
· 截面二次轴矩
定义截面的面积为A,则分别表示截面对坐标轴x与y的惯性矩,第一式中的y和第二式中的x分别表示面积微元dA到x和到y轴的垂直距离。在国际单位制(SI)中,截面二次轴矩的单位是m,常用mm表示。坐标变换计算截面惯性矩时常根据截面形状采用方便计算的坐标系,然后可以通过坐标变换应用到其他坐标系中。平行轴定理在已知对过截面形心轴的惯性矩和轴间距离的情况下,平行轴定理可以确定对变换后新轴的惯性矩。Ix:对x轴的惯性矩IxCG:对与x轴平行并且过截面形心的轴(与中性轴重合)的惯性矩A:截面面积d:两轴之间的距离转轴公式下列公式可以计算坐标轴旋转一个角度后截面对新坐标轴的惯性矩ϕϕ-->{\displaystyle\phi}:旋转的角度(逆时针)Ix和Iy:原坐标系下的惯性矩Ix和Iy:坐标系转动后新坐标系下的惯性矩简单截面的惯性矩以下是几种简单截面对"截面形心"所在轴的惯性矩矩形截面b:宽度(x方向)h...
知识互答
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信
























{{item.time}} {{item.replyListShow ? '收起' : '展开'}}评论 {{curReplyId == item.id ? '取消回复' : '回复'}}