基本相互作用

强、弱、电磁和引力四种基本相互作用中的耦合常数的大小大致如下 ：

弱耦合与微扰论

如果一个问题中的耦合常数 g {\displaystyle g} 远小于单位一，则其称为“弱耦合”的，此时问题的解 A {\displaystyle A} 可以按照 g {\displaystyle g} 的幂次（又叫做阶数）展开表示为，

其中， A 0 {\displaystyle A_{0}} 为没有相互作用时问题的解。这种方法称为微扰论。在上述微扰展开中，越高阶项的贡献越小。因而可以在适当阶做截断，以满足给定的精度要求。微扰论只有在弱耦合时才有用，因为若耦合常数 g {\displaystyle g} 大于一，则越高阶项的贡献越大，任何有限阶数的截断都会带来严重的误差。

微扰论在量子场论中具有核心地位。量子场论中的微扰论计算一般是通过费曼图和费曼规则来系统地组织实现的，因为费曼图就是按照耦合常数的幂次画出来的。电磁相互作用、弱相互作用在寻常尺度下都是弱耦合的相互作用。而强相互作用在短距离上（尺度远小于飞米时）也是弱耦合的。

跑动的耦合常数

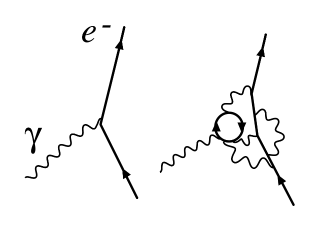
在量子力学尤其是量子场论中，由于量子涨落效应的存在，相互作用顶点被虚粒子所修正，成为非定域性的相互作用顶点。因此，测得的耦合常数的大小与原拉格朗日量或哈密顿量中的裸耦合常数不同，且与测量的能量标度有关。后一点可以通过不确定关系， Δ Δ --> p Δ Δ --> x ≥ ≥ --> 1 2 ℏ ℏ --> {\displaystyle \Delta p\Delta x\geq {\frac {1}{2}}\hbar } 来理解。测量使用的能量越高，测量仪器能够分辨的尺度就越小。在小尺度下，将能看到更多的虚粒子的涨落。这种效应与电荷在介质中的极化效应是相似的。因而也被称为真空极化。这种随着能标的改变而改变的“耦合常数”被称为 跑动的耦合常数 。

β函数β( g ) 描述了耦合常数随能量标度 μ 变化的的情形，其定义如下

其中μ为特定物理过程的能量标度。

若量子场论中的β函数为零，则此理论为共形场论。若在高能量下β函数为正，代表耦合常数随着能标的增加而增加；若在高能量下β函数为负，则代表耦合常数随着能标的增加减小，这种现象叫做 渐近自由 。

量子电动力学和朗道奇点

根据微扰论，描写电磁相互作用的量子电动力学的β函数为正，耦合效应会随着能量增加而增强。量子电动力学在高能量时会变得高度耦合，甚至在某些有限时能量下，耦合系数似乎会变成无限大，此现象最早是由列夫·达维多维奇·郎道所发现，因此称为 郎道奇点 （ 英语 ： Landau pole ） 。不过微扰论在强耦合情况下已经失效。而且达到朗道奇点所需的能标远远超过普朗克能标，而一般认为量子场论在普朗克能标左右已经不再适用。

量子色动力学和渐近自由

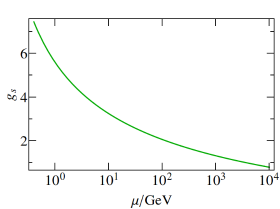
精确到 g s 2 {\displaystyle g_{s}^{2}} 阶的强相互作用的耦合常数随着能标的变化

弗朗克·韦尔切克、休·波利策及戴维·格娄斯发现，描写强相互作用的量子色动力学的β函数为负。因此量子色动力学的耦合在高能量时会降低。其发现者因此获得2004年的诺贝尔物理奖 。在一阶近似下耦合系数大致可以表示为下式：

其中 β β --> 0 = 1 12 π π --> ( 33 − − --> 2 N f ) {\displaystyle \beta _{0}={\frac {1}{12\pi }}(33-2N_{f})} 为一常数， N f = 6 {\displaystyle N_{f}=6} 是夸克味的数目。这是最先由韦尔切克、波利策和格娄斯计算的。

相反的，耦合程度会随着能量降低而增强，因此在低能量时耦合效应会变强。尤其是在能标 Λ 上由微扰论定义耦合常数开始出现发散，因此不能用微扰效应来求解。 Λ 称为QCD尺度，其数值为

大致对应于一飞米。

弦理论

弦理论下的耦合常数有明显的不同点，弦耦合常数一方面意味着决定一根弦分裂的能力，另一方面则意味着弦理论的每一个微扰叙述和一个弦耦合常数有关，可是这些耦合常数不是事先定义、可调整及共适性的常数，而是动态的标量场，会依位置和时间改善，而其数值需动态决定。

相关条目

耦合 (物理学)

量子场论、量子电动力学及量子色动力学

规范量子化 （ 英语 ： Canonical quantization ） 、重整化及 维度正则化 （ 英语 ： Dimensional regularization ）

精细结构常数

重力耦合常数 （ 英语 ： Gravitational coupling constant ）

费米耦合常数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。