定义

菲涅耳积分可由下面两个级数求得，对所有x均收敛。

羊角螺线

估计值

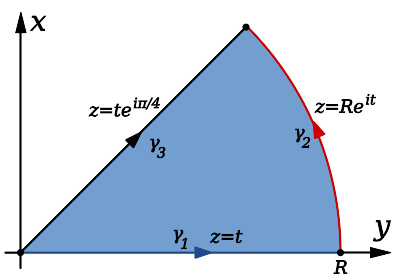
用来计算Fresnel integrals的扇形路径

C和S的值当变数趋近于无穷大时，可用复变分析的方法求得。用以下这个函数的路径积分：

在复数平面上的一个扇型的边界，其中下边绕着正x轴，上半边是沿着y = x, x ≥ 0的路径，外圈则是一个半径为R，中心在原点的弧形。

当R趋近于无穷大时，路径积分沿弧形的部分将趋近于零，而实数轴部分的积分将可由高斯积分

并且经过简单的计算后，第一象限平分线的那条积分便可以变成菲涅耳积分。

相关公式

下列一些包含菲涅耳积分的关系式

∫ ∫ -->0∞ ∞ -->e− − -->atsin(t2){\displaystyle \int _{0}^{\infty }e^{-at}sin(t^{2})}=(1/4)∗ ∗ -->(2)∗ ∗ -->(π π -->)∗ ∗ -->(cos((1/4)∗ ∗ -->a2)∗ ∗ -->(1− − -->2∗ ∗ -->FresnelC((1/2)∗ ∗ -->a∗ ∗ -->(2)/(π π -->)))+sin((1/4)∗ ∗ -->a2)∗ ∗ -->(1− − -->2∗ ∗ -->FresnelS((1/2)∗ ∗ -->a∗ ∗ -->(2)/(Pi)))){\displaystyle =(1/4)*{\sqrt {(}}2)*{\sqrt {(}}\pi )*(cos((1/4)*a^{2})*(1-2*FresnelC((1/2)*a*{\sqrt {(}}2)/{\sqrt {(}}\pi )))+sin((1/4)*a^{2})*(1-2*FresnelS((1/2)*a*{\sqrt {(}}2)/{\sqrt {(}}Pi))))}

∫ ∫ -->(sin(ax2+2bx+c)dx={\displaystyle \int (sin(ax^{2}+2bx+c)dx=}(2)∗ ∗ -->(π π -->)∗ ∗ -->(cos((b2− − -->a∗ ∗ -->c)/a)∗ ∗ -->FresnelS((2)∗ ∗ -->(a∗ ∗ -->x+b)/((π π -->)∗ ∗ -->(a)))− − -->sin((b2− − -->a∗ ∗ -->c)/a)∗ ∗ -->FresnelC((2)∗ ∗ -->(a∗ ∗ -->x+b)/((π π -->)∗ ∗ -->(a))))2(a){\displaystyle {\frac {{\sqrt {(}}2)*{\sqrt {(}}\pi )*(cos((b^{2}-a*c)/a)*FresnelS({\sqrt {(}}2)*(a*x+b)/({\sqrt {(}}\pi )*{\sqrt {(}}a)))-sin((b^{2}-a*c)/a)*FresnelC({\sqrt {(}}2)*(a*x+b)/({\sqrt {(}}\pi )*{\sqrt {(}}a))))}{2{\sqrt {(}}a)}}}

∫ ∫ -->(FresnelC(t)dt=FresnelC(t)∗ ∗ -->t− − -->sin((1/2)∗ ∗ -->π π -->∗ ∗ -->t2)π π -->{\displaystyle \int (FresnelC(t)dt=FresnelC(t)*t-{\frac {sin((1/2)*\pi *t^{2})}{\pi }}}

∫ ∫ -->(FesnelS(t)dt=FresnelS(t)∗ ∗ -->t+cos((1/2)∗ ∗ -->π π -->∗ ∗ -->t2)π π -->{\displaystyle \int (FesnelS(t)dt=FresnelS(t)*t+{\frac {cos((1/2)*\pi *t^{2})}{\pi }}}

dFresnelC(t)dt=cos((1/2)∗ ∗ -->π π -->∗ ∗ -->t2){\displaystyle {\frac {dFresnelC(t)}{dt}}=cos((1/2)*\pi *t^{2})}

dFresnelS(t)dt=sin((1/2)∗ ∗ -->π π -->∗ ∗ -->t2){\displaystyle {\frac {dFresnelS(t)}{dt}}=sin((1/2)*\pi *t^{2})}

关联条目

奥古斯丁·菲涅耳

羊角螺线

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。