凸集实例

区间是实数的凸集。

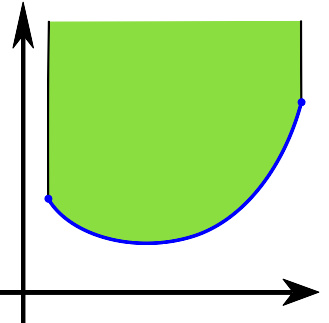
依据定义，中空的圆形称为圆（circle），它不是凸集；实心的圆形称为圆盘（disk），它是凸集。

凸多边形是欧几理得平面上的凸集，它们的每只角都小于180度。

单纯形是凸集，对于单纯形的顶点集合来说，单纯形是它们的最小凸集，所以单纯形也是一个凸包。

定宽曲线是凸集。

凸集的延森不等式定义

在度量几何中，琴生不等式（Jensen"s inequality）为凸集给出一个最健全的解释，而不必牵涉到二阶导数：

简单而言，就是 S {\displaystyle S} 中的任何两点之间的直线段都属于 S {\displaystyle S} 。因此，凸集是一个连通空间。

特殊凸集

特殊凸集是特别给了名称的凸集，它们可能是具有额外性质的凸集，或是在某种定义下的凸集（非一般定义中的凸集）。

具有额外性质的凸集

绝对凸集：若 S {\displaystyle S} 既是凸集又是平衡集，则称 S {\displaystyle S} 为 绝对凸 的。

在某种定义下的凸集

星形凸集：若集 S {\displaystyle S} 中存在一点 x 0 {\displaystyle x_{0}} ，使得由 x 0 {\displaystyle x_{0}} 到 S {\displaystyle S} 中任何一点的直线段都属于 S {\displaystyle S} ，则称 S {\displaystyle S} 为 星形域 或 星形凸集 。星形域是简单连通的。

性质

若 S {\displaystyle S} 是凸集，对于任意 u 1 , u 2 , … … --> , u r ∈ ∈ --> S {\displaystyle u_{1},u_{2},\ldots ,u_{r}\in S} ，及所有非负数 λ λ --> 1 , λ λ --> 2 , … … --> , λ λ --> r {\displaystyle \lambda _{1},\lambda _{2},\ldots ,\lambda _{r}} 满足 λ λ --> 1 + λ λ --> 2 + ⋯ ⋯ --> + λ λ --> r = 1 {\displaystyle \lambda _{1}+\lambda _{2}+\cdots +\lambda _{r}=1} ，都有 ∑ ∑ --> k = 1 r λ λ --> k u k ∈ ∈ --> S {\displaystyle \sum _{k=1}^{r}\lambda _{k}u_{k}\in S} 。这个向量称为 u 1 , u 2 , … … --> , u r {\displaystyle u_{1},u_{2},\ldots ,u_{r}} 的 凸组合 。

非欧几何的凸集

对于非欧平面，可用测地线来取代在欧几理德凸集的定义内直线段。

参见

凸函数

凸包

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。