



广义黎曼猜想
广义黎曼猜想狄利克雷L函数下的广义黎曼猜想最初可能是由皮尔茨(Piltz)于1884年提出的。与原始的黎曼猜想类似,该猜想对研究素数分布十分重要。如查一个已知的狄利克雷特征χ,可以定义如下狄利克雷L函数其中,s为实部大于1的所有复数。这一函数可以解析延宕为整个复平面上的亚纯函数。广义黎曼猜想即是指,狄利克雷L函数L(χ,s)的所有非平凡零点的实部都为1/2。当对所有n都有χ(n)=1时,广义黎曼猜想退化为普通的黎曼猜想。扩展黎曼猜想假设K为数域(有理数域的有限次代数扩张域),OK为K的整数环,a为OK的理想,Na则为非零理想的绝对范数。于是可以定义K上的戴德金ζ函数其中,s为实部大于1的所有复数。求和运算对OK的所有非零理想a进行。这一函数也可以解析延宕到整个复平面上。扩展黎曼猜想是指,戴德金ζ函数ζK(s)的所有非平凡零点的实部都为1/2。当数域K取有理数域Q,其整数环则为Z时,扩展黎曼...
广义黎曼猜想
狄利克雷L函数下的广义黎曼猜想最初可能是由皮尔茨(Piltz)于1884年提出的。与原始的黎曼猜想类似,该猜想对研究素数分布十分重要。
如查一个已知的狄利克雷特征χ,可以定义如下狄利克雷L函数
其中,s为实部大于1的所有复数。这一函数可以解析延宕为整个复平面上的亚纯函数。广义黎曼猜想即是指,狄利克雷L函数L(χ,s)的所有非平凡零点的实部都为1/2。
当对所有n都有χ(n) = 1时,广义黎曼猜想退化为普通的黎曼猜想。
扩展黎曼猜想
假设K为数域(有理数域的有限次代数扩张域),OK为K的整数环,a为OK的理想,Na则为非零理想的绝对范数。于是可以定义K上的戴德金ζ函数
其中,s为实部大于1的所有复数。求和运算对OK的所有非零理想a进行。
这一函数也可以解析延宕到整个复平面上。扩展黎曼猜想是指,戴德金ζ函数ζK(s)的所有非平凡零点的实部都为1/2。
当数域K取有理数域Q,其整数环则为Z时,扩展黎曼猜想退化为普通的黎曼猜想。
参考文献
Hazewinkel, Michiel (编),Riemann hypothesis, generalized,数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
推荐阅读
· 黎曼猜想

历史黎曼ζ函数在临界线Re(s)=1/2上的实部(红色)和虚部(蓝色)。我们可以看到最起初的几个非平凡零点就位于Im(s)=±14.135,±21.022和±25.011上。黎曼ζ函数实部与虚部的数值比较图,也就是Re(ζ(s))vs.Im(ζ(s)),沿着临界线s=it+1/2,t由0到34黎曼1859年在他的论文《ÜberdieAnzahlderPrimzahlenuntereinergegebenenGröße》中提及了这个著名的猜想,但它并非该论文的中心目的,他也没有试图给出证明。黎曼知道ζ函数的不平凡零点对称地分布在直线s=½+it上,以及他知道它所有的不平凡零点一定位于区域0≤Re(s)≤1中。1896年,雅克·阿达马和CharlesJeandelaVallée-Poussin分别独立地证明了在直线Re(s)=1上没有零点。连同了黎曼对于不非凡零点已经证明了的其他特性,这显示了...
· 黎曼猜想为什么危险猜想危险在什么地方
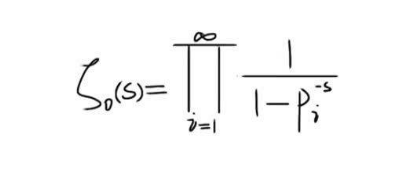
都在等待“黎曼猜想”证明却不知道它后面隐藏的危险一、大神黎曼过直线外一点,可作其几条平行线?欧氏几何说,只能作一条;罗氏几何说,至少可以作两条(包括一组和无数)。黎曼慢悠悠地反问:谁知道平行线相交还是不相交呢?“平行线公理”的世纪之争,最终终结于黎曼。黎曼提出:过直线外一点,一条平行线也作不出来。(这是人话吗?)可基于黎曼几何得出的“无平行线”结论,最终成了广义相对论的数学帮手。广义相对论最初源于爱因斯坦意识到引力并不是一种力,而是时空几何弯曲的体现。物理直觉超于常人的爱因斯坦一直找不到数学工具来表达他的想法,如果没有数学支撑,直接说引力是时空弯曲效应,肯定会被吐槽成“物理是体育老师教的”。所以,直到他从数学界朋友了解到黎曼的“非欧几何”,才让广义相对论提早问世。当爱因斯坦得意地跟全世界说:如果没有我,50年内也不会出现广义相对论。这时候,能和爱因斯坦站在一起吹牛的,也只有数学大神黎曼了。...
· 黎曼在创造绝世猜想之前都做过哪些事情

高斯:黎曼的论文提供了令人信服的证据,作者对该文所论述的这一问题作了全面深入的研究。作者具有创造性的、活跃的、真正数学家的头脑,具有灿烂丰富的创造力。昨天,全世界最杰出的数学家之一:迈克尔·阿提亚就证明黎曼猜想发表论述。在此之前,黎曼算不上广为人知,但数学天才高斯的大名却如雷贯耳。高斯对学术要求极其严格,并且一向吝于对别人发出赞美,黎曼是怎么做到的?黎曼出生在德国北部的一个小镇。从小家庭贫困,加之体弱多病、性格孤僻,黎曼的童年远远谈不上幸福。逆境也无法遮挡天赋的光芒。小学时,黎曼就时常用惊人的心算能力让老师叹服。中学时,黎曼得到了老师的赏识,老师特许黎曼在自己的私人图书馆里自由借阅书籍。一次,黎曼借取了法国数学家勒让德的著作《数论》。这本800多页的著作极其晦涩难懂,但黎曼仅用了一周便研习透彻。那时他才14岁。由于父亲是牧师,黎曼对宗教也怀有极大热忱。高中毕业后,他开始学习语言学和神学,打...
· 黎曼流形
参看黎曼几何芬斯勒流形黎曼子流形假黎曼流形参考JurgenJost,RiemannianGeometryandGeometricAnalysis,(2002)Springer-Verlag,BerlinISBN3-540-4267-2
· 广义省
行政区划广义省下辖1市13县。广义市(ThànhphốQuảngNgãi)波澌县(HuyệnBaTơ)平山县(HuyệnBìnhSơn)德普县(HuyệnĐứcPhổ)明隆县(HuyệnMinhLong)慕德县(HuyệnMộĐức)义行县(HuyệnNghĩaHành)山河县(HuyệnSơnHà)山西县(HuyệnSơnTây)山静县(HuyệnSơnTịnh)西茶县(HuyệnTâyTrà)茶芃县(HuyệnTràBồng)思义县(HuyệnTưNghĩa)理山县(HuyệnLýSơn)
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















