概念

假设有一束射出的粒子，另有一个由某种材料制成的平面状箔，粒子以垂直于这个平面的方向射来。平面箔上被击中的微粒在平面上代表的面积，即为所说的“截面”，用希腊字母σ σ -->{\displaystyle \sigma }表示。这些粒子在接近目标粒子所组成的薄面时，会发生一些相互作用。

这个术语起源于点粒子被射向固体目标的经典物理图景。假设发射粒子与目标粒子一旦靠近就一定会发生相互作用，如果错失了就完全不发生相互作用，则总的相互作用可能性就等于截面与整个靶面积的比值。

上述的基本概念可以引申到其他的情况，例如靶区域呈现介于0至100%反应几率的情况——因为目标中的物质不完全相同，或者因为不均匀的场使之减弱。一个特殊的例子就是散射。

散射截面

散射截面σ σ -->scat{\displaystyle {\sigma }_{scat}}是用于描述光（或者其他形式的辐射）被粒子散射的可能性。一般地说，散射截面里所指的“截面”与几何上的“截面”不同，它与入射波长的波长和靶粒子的电容率、形状、大小有关。稀疏介质的散射总数决定于散射截面和粒子个数的乘积。考虑到吸收、散射和发光，总散射截面（σ σ -->{\displaystyle {\sigma }}）可以用面积表示为下面的式子：

根据比尔－朗伯定律，吸光度与浓度成比例，即Aλ λ -->=Cℓ ℓ -->σ σ -->{\displaystyle A_{\lambda }=C\,\ell \,\sigma }，其中C{\displaystyle C}是浓度，Aλ λ -->{\displaystyle A_{\lambda }}为给定波长λ λ -->{\displaystyle \lambda }的吸光度，ℓ ℓ -->{\displaystyle \ell }为路径长度，由此总散射面积还与光的吸光度有关。入射辐射的吸光度是透光率倒数的对数：

在考虑粒子的散射时，通常引入另一个物理量微分散射截面，而将σ σ -->{\displaystyle \sigma }称作总散射截面。微分散射截面表达为：

其中Ω Ω -->{\displaystyle \Omega }为出射粒子的空间角。这个微分表示每单位空间角的出射粒子对应的入射区域，因此对这个量在一个完整的空间角中积分即可获得总截面。微分散射截面在量子力学中可方便地由∣ ∣ -->f(θ θ -->)∣ ∣ -->2{\displaystyle \mid f(\theta )\mid ^{2}}求得；而f(θ θ -->){\displaystyle f(\theta )}由量子力学中散射结果，进行渐近分析分解为入射波与散射波后（如用分波方法分解为球谐函数，或玻恩近似），设定入射项的系数为1，出射项系数即为f(θ θ -->)/r{\displaystyle f(\theta )/r}。

原子核物理图

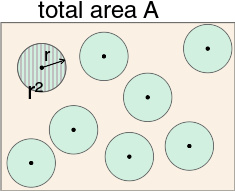
原子核物理学中截面的示意图

在原子核物理学中，截面的概念可以很方便地表达特定事件发生的可能性。在统计上，薄膜上原子的中心可以被看做均匀分布在一个平面上的点的集合。参与撞击原子的中心与其他原子以r{\displaystyle r}为距离通过的概率是确定的。事实上，如果在平面上A{\displaystyle A}区域有n{\displaystyle n}个原子中心，那么这个概率为(nπ π -->r2)/A{\displaystyle (n\pi r^{2})/A}，这仅仅是所有原子中心以r{\displaystyle r}为半径的圆的总面积与整个平面的比值。如果我们将原子考虑成不可穿透的钢制盘，将与之相互作用的粒子看做直径可以忽略的子弹，这个比值就是“子弹”被“钢质盘”截止的可能性，也就是说入射粒子被被射原子平面阻挡的的可能性。如果计算通过的原子，那么结果则可以被表达为原子的等效截止截面。这一概念可以延伸到任何有关入射粒子与靶粒子间的相互作用。例如入射粒子阿尔法粒子轰击靶粒子铍会产生中子的可能性可以表示原子种原子核反应的反应截面。

参考文献

J.D.Bjorken, S.D.Drell, Relativistic Quantum Mechanics, 1964

P.Roman, Introduction to Quantum Theory, 1969

W.Greiner, J.Reinhardt, Quantum Electrodinamics, 1994

R.G. Newton. Scattering Theory of Waves and Particles. McGraw Hill, 1966.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。