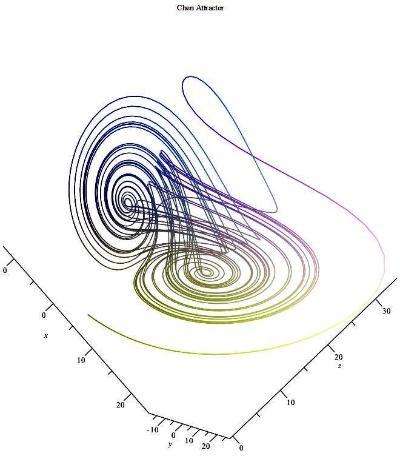
数值解Chen吸引子利用龙格－库塔法可以求得陈氏系统的混沌吸引子图形和波形：右图陈氏吸引子的参数：初始条件：a=35,c=27,b=2.8,x(0)=-.1,y(0)=.3,z(0)=-.6参看吸引子混沌理论广义陈氏吸引子

参看

简述洛伦茨方程的一条轨迹被描绘成金属线，以展现方向以及三维结构洛伦茨吸引子及其导出的方程组是由爱德华·诺顿·洛伦茨于1963年发表，最初是发表在《大气科学杂志》（JournaloftheAtmosphericSciences）杂志的论文《DeterministicNonperiodicFlow》中提出的，是由大气方程中出现的对流卷方程简化得到的。这一洛伦茨模型不只对非线性数学有重要性，对于气候和天气预报来说也有着重要的含义。行星和恒星大气可能会表现出多种不同的准周期状态，这些准周期状态虽然是完全确定的，但却容易发生突变，看起来似乎是随机变化的，而模型对此现象有明确的表述。从技术角度看来，洛伦茨振子具有非线性、三维性和确定性。2001年，沃里克·塔克尔（WarwickTucker）证明出在一组确定的参数下，系统会表现出混沌行为，显示出人们今天所知的奇异吸引子。这样的奇异吸引子是豪斯多夫维数在

参考资料《史记·高祖功臣侯者年表》《汉书·高惠高后文功臣表》

吸(xī)姓【摘要】吸姓的记载最早见于第三次全国人口普查资料。〔姓源〕其姓源各姓氏书未知其源,广西壮族自治区人口普查资料有吸姓。〔供橱〕吸姓祖宗神位供奉在大槐树祭祖堂七号供橱。吸姓的记载最早见于第三次全国人口普查资料。〔姓源〕其姓源各姓氏书未知其源,广西壮族自治区人口普查资料有吸姓。〔供橱〕吸姓祖宗神位供奉在大槐树祭祖堂七号供橱。