定义及运算律

外代数有很多种等价的定义，下面的定义是最简洁的一个。

定义: 设 V{\displaystyle V} 是域 K{\displaystyle K} 上的一个向量空间，让 Tk(V):=V⊗ ⊗ -->⋯ ⋯ -->⊗ ⊗ -->V⏟ ⏟ -->k{\displaystyle T^{k}(V):={\underset {k}{\underbrace {V\otimes \cdots \otimes V} }}} 则定义

令 I{\displaystyle I} 为 V{\displaystyle V} 的张量代数的理想（即双边理想），该理想是由所有形如 v⊗ ⊗ -->v{\displaystyle v\otimes v} 的张量生成的（其中 v∈ ∈ -->V{\displaystyle v\in V} 任意），则将 V{\displaystyle V} 上的外代数 Λ Λ -->(V){\displaystyle \Lambda (V)} 定义为商代数 T(V)/I{\displaystyle T(V)/I}，即

并且把 v1⊗ ⊗ -->… … -->⊗ ⊗ -->vk∈ ∈ -->TkV{\displaystyle v_{1}\otimes \ldots \otimes v_{k}\in T^{k}V} 的等价类[v1⊗ ⊗ -->… … -->⊗ ⊗ -->vk]∈ ∈ -->T(V)/I{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in T(V)/I} 记为 v1∧ ∧ -->… … -->∧ ∧ -->vk{\displaystyle v_{1}\wedge \ldots \wedge v_{k}}，其中 v1,… … -->,vk∈ ∈ -->V{\displaystyle v_{1},\ldots ,v_{k}\in V}. 设 k=0,1,2,… … -->,{\displaystyle k=0,1,2,\ldots \,,} 称

为 V{\displaystyle V} 的 k{\displaystyle k}-阶外幂（k{\displaystyle k}th exterior power of V{\displaystyle V}），称 Λ Λ -->k(V){\displaystyle \Lambda ^{k}(V)} 中的元素为 k{\displaystyle k}-向量（k{\displaystyle k}-multivector）。

注：

∀ ∀ -->λ λ -->∈ ∈ -->K{\displaystyle \forall \lambda \in K}，当且仅当 λ λ -->=0{\displaystyle \lambda =0} 时才有 λ λ -->∈ ∈ -->I{\displaystyle \lambda \in I}，因此，可以把 Λ Λ -->0(V)=K/I{\displaystyle \Lambda ^{0}(V)=K/I} 等同于 K{\displaystyle K}，并且把 [λ λ -->]∈ ∈ -->Λ Λ -->0(V){\displaystyle [\lambda ]\in \Lambda ^{0}(V)} 记为 λ λ -->{\displaystyle \lambda }；基于类似的原因，可以把 Λ Λ -->1(V)=V/I{\displaystyle \Lambda ^{1}(V)=V/I} 等同于 V{\displaystyle V}，而且把 [v]∈ ∈ -->Λ Λ -->0(V){\displaystyle [v]\in \Lambda ^{0}(V)} 记为 v{\displaystyle v}。这一点是前面所讲的能够把 [v1⊗ ⊗ -->… … -->⊗ ⊗ -->vk]∈ ∈ -->Λ Λ -->k(V){\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in \Lambda ^{k}(V)} 记为 v1∧ ∧ -->… … -->∧ ∧ -->vk{\displaystyle v_{1}\wedge \ldots \wedge v_{k}} 的特例和前提。

当 k>1{\displaystyle k>1} 时，k{\displaystyle k}-向量并不仅限于形如 v1∧ ∧ -->… … -->∧ ∧ -->vk{\displaystyle v_{1}\wedge \ldots \wedge v_{k}} 的元素，例如，v1∧ ∧ -->v2+w1∧ ∧ -->w2{\displaystyle v_{1}\wedge v_{2}+w_{1}\wedge w_{2}} 也是 2-向量，其中 v1,v2,w1,w2∈ ∈ -->V{\displaystyle v_{1},v_{2},w_{1},w_{2}\in V}.

理想 I{\displaystyle I} 中的元素并不仅限于形如 v⊗ ⊗ -->v{\displaystyle v\otimes v} 的张量，例如，

设 k=2,3,… … -->{\displaystyle k=2,3,\ldots }，则 ∀ ∀ -->α α -->∈ ∈ -->Λ Λ -->k(V){\displaystyle \forall \alpha \in \Lambda ^{k}(V)}，α α -->{\displaystyle \alpha对称 作为等价类含有唯一的一个完全反对称的代表元 t∈ ∈ -->Tk(V){\displaystyle t\in T^{k}(V)}，可以把这个 k{\displaystyle k}-阶的完全反对称张量等同于 α α -->{\displaystyle \alpha }, 详见后面的“反对称算子和外幂”一节。在有些文献中，k{\displaystyle k}-向量就是以这种方式定义的。

运算律 将上面的注中的内容用 ∧ ∧ -->{\displaystyle \wedge } 写出，则分别给出

(1) ∀ ∀ -->λ λ -->∈ ∈ -->K,α α -->∈ ∈ -->Λ Λ -->(V){\displaystyle \forall \lambda \in K,\alpha \in \Lambda (V)}, λ λ -->∧ ∧ -->α α -->=α α -->∧ ∧ -->λ λ -->=λ λ -->α α -->.{\displaystyle \lambda \wedge \alpha =\alpha \wedge \lambda =\lambda \alpha .}

证明如下： 作为等价类，我们从 α α -->∈ ∈ -->Λ Λ -->(V)=T(V)/I{\displaystyle \alpha \in \Lambda (V)=T(V)/I} 中任意挑选一个代表元 t{\displaystyle t}，则 t∈ ∈ -->T(V){\displaystyle t\in T(V)} 而且 α α -->=[t].{\displaystyle \alpha =[t].} 根据商代数的定义，

类似地，可以证明 α α -->∧ ∧ -->λ λ -->=λ λ -->α α -->.{\displaystyle \alpha \wedge \lambda =\lambda \alpha \,.}

(2) 根据注 3.1 中的内容，显然有 v∧ ∧ -->v=0,∀ ∀ -->v∈ ∈ -->V{\displaystyle v\wedge v=0,\,\forall v\in V}.

(3) 根据注 3.2 中的内容，对任意 v,w∈ ∈ -->V{\displaystyle v,w\in V} 成立着

注：即使 K{\displaystyle K} 的特征为 2，这个公式也是对的，只不过此时有 − − -->1=1{\displaystyle -1=1} 而已。

(4) 根据商代数的定义以及张量代数的性质，运算 ∧ ∧ -->:Λ Λ -->(V)× × -->Λ Λ -->(V)→ → -->Λ Λ -->(V){\displaystyle \wedge :\Lambda (V)\times \Lambda (V)\rightarrow \Lambda (V)} 满足结合律和分配律：

其中 α α -->,β β -->,θ θ -->∈ ∈ -->Λ Λ -->(V){\displaystyle \alpha ,\beta ,\theta \in \Lambda (V)} 都是任意的。

以前两条性质为例，其证明如下：设张量 a,b,t∈ ∈ -->T(V){\displaystyle a,b,t\in T(V)} 分别是 α α -->,β β -->,θ θ -->{\displaystyle \alpha ,\beta ,\theta } 中的代表元，即 α α -->=[a]{\displaystyle \alpha =[a]}, β β -->=[b]{\displaystyle \beta =[b]}, θ θ -->=[t]{\displaystyle \theta =[t]}, 则

(5) 根据上面的 (3) 和 (4)，用数学归纳法可以证明：∀ ∀ -->α α -->∈ ∈ -->Λ Λ -->k(V),β β -->∈ ∈ -->Λ Λ -->l(V),{\displaystyle \forall \alpha \in \Lambda ^{k}(V)\,,\,\beta \in \Lambda ^{l}(V)\,,}

证明从略。

基底和维数

若V的维数是n而{e1,...,en}是V的基，则集合

是k阶外幂Λ(V)的一个基。理由如下：给定任何如下形式的楔积

则每个向量vj可以记为基向量ei的一个线性组合;利用楔积的双线性性质，这可以扩张为那些基向量的楔积的线性组合。任何出现同样基向量两次的楔积为0；任何基向量出现的次序不正确的可以重新排序，在交换任何两个基向量的时候变换符号。一般来讲，最后基k-向量前的系数可以用通过积ei来描述vj的矩阵的子式来计算。

数一下基元素，我们可以看到Λ(V) 的维数是n 取 k。特别的有， Λ(V) = {0} 对于 k > n.

外代数是一个分级代数，是如下直和

其维数等于二项式系数之和，也就是2.

例子: 欧氏三维空间的外代数

考虑空间R，其基为{i, j, k}。一对向量

的楔积为

其中{i ∧ j, i ∧ k, j ∧ k}是三维空间Λ(R)的基底。

再加一个向量

这三个向量的楔积是

其中i ∧ j ∧ k是一维空间Λ(R)的基底。

空间Λ(R) 是R, 而空间Λ(R) 是R。取所有四个子空间的直和得到一个向量空间Λ(R)，这是八维向量空间

那么，给定一对8维向量a和b, 其中a如上给出，而

a和b的楔积如下(用列向量表达),

容易验证8维楔积以向量(1,0,0,0,0,0,0,0)为乘法幺元。也可以验证该Λ(R)代数的楔积是结合的(也是双线性的):

所以该代数是有单位且结合的。

叉乘的实质，赝向量与赝标量

对三维欧几里得空间 E3{\displaystyle E^{3}} 可以建立一个线性同构 ϕ ϕ -->:Λ Λ -->2(E3)→ → -->E3{\displaystyle \phi :\Lambda ^{2}(E^{3})\rightarrow E^{3}} 如下：任取 E3{\displaystyle E^{3}} 的右手的标准正交基 i{\displaystyle {\boldsymbol {i}}}，j{\displaystyle {\boldsymbol {j}}}，k{\displaystyle {\boldsymbol {k}}}，规定 ϕ ϕ -->{\displaystyle \phi } 把 i∧ ∧ -->j{\displaystyle {\boldsymbol {i}}\wedge \mathbf {j} }，j∧ ∧ -->k{\displaystyle {\boldsymbol {j}}\wedge {\boldsymbol {k}}}，k∧ ∧ -->i{\displaystyle {\boldsymbol {k}}\wedge {\boldsymbol {i}}} 分别映射为 k{\displaystyle {\boldsymbol {k}}}，i{\displaystyle {\boldsymbol {i}}}，j{\displaystyle {\boldsymbol {j}}}，则 ϕ ϕ -->{\displaystyle \phi } 的定义与右手的标准正交基如何选取无关。

不难看出，对任意向量 u{\displaystyle {\boldsymbol {u}}} 和 v{\displaystyle {\boldsymbol {v}}}，这个线性同构把 u∧ ∧ -->v{\displaystyle {\boldsymbol {u}}\wedge {\boldsymbol {v}}} 映射为 u× × -->v{\displaystyle {\boldsymbol {u}}\times {\boldsymbol {v}}}。这就是叉乘（向量积）的实质。例如，E3{\displaystyle E^{3}} 中平行四边形ABCD{\displaystyle ABCD} 的面积向量可以表示为 AB→ → -->× × -->AD→ → -->{\displaystyle {\overrightarrow {AB}}\times {\overrightarrow {AD}}}，推广之后，高维黎曼流形(M,g){\displaystyle (M,\mathbf {g} )} 中的紧的二维曲面 Σ Σ -->{\displaystyle \Sigma } 的面积用

来计算（其中 hab{\displaystyle h_{ab}} 是度规张量场 g{\displaystyle \mathbf {g} } 在 Σ Σ -->{\displaystyle \Sigma } 上的诱导度规 h=habdua⊗ ⊗ -->dub{\displaystyle \mathbf {h} =h_{ab}\,du^{a}\otimes du^{b}} 的坐标分量），由此可以看到外积和叉乘的渊源关系。

物理学中经常要区分的向量（极向量）与赝向量（轴向量）这两个概念，现在就容易理解了：从根本上说，向量是 E3{\displaystyle E^{3}} 中的元素，所以在空间反演变换下会改变方向；而赝向量其实是 Λ Λ -->2(E3){\displaystyle \Lambda ^{2}(E^{3})} 中的元素，在空间反演变换下不会改变方向。

类似地，借助于右手的标准正交基，可以把 Λ Λ -->3(E3){\displaystyle \Lambda ^{3}(E^{3})} 中的元素 ai∧ ∧ -->j∧ ∧ -->k{\displaystyle a\,{\boldsymbol {i}}\wedge {\boldsymbol {j}}\wedge {\boldsymbol {k}}} 映射为“标量" a∈ ∈ -->R=Λ Λ -->0(E3){\displaystyle a\in \mathbb {R} =\Lambda ^{0}(E^{3})}。但是，在空间反演变换下它就会原形毕露，所以称它为赝标量。真正的标量在空间反演下是不变的，而赝标量在空间反演下会改变符号。

把 2-向量 u∧ ∧ -->v{\displaystyle {\boldsymbol {u}}\wedge {\boldsymbol {v}}} 映射为向量 u× × -->v{\displaystyle {\boldsymbol {u}}\times {\boldsymbol {v}}} 以及把 3-向量 ai∧ ∧ -->j∧ ∧ -->k{\displaystyle a\,{\boldsymbol {i}}\wedge {\boldsymbol {j}}\wedge {\boldsymbol {k}}} 映射为一个实数 a{\displaystyle a} 的映射实际上是一个叫做霍奇对偶的线性映射。

泛性质及构造

令V为一个域K（在多数应用中，也就是实数域）上的向量空间。Λ(V)是“最一般”的包含 V 的并有一个交替乘法在V上由单位的结合K-代数这个事实可以用如下的泛性质形式化的表达：

任给一个有单位的结合 K-代数 A 和一个 K-线性映射j : V → A 使得 j(v)j(v) = 0 对于每个 v 属于 V 成立，则存在恰好一个由单位的代数同态f : Λ(V) → A 使得 f(v) = j(v) 所有 v 属于 V 成立。

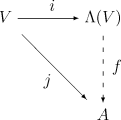
要构造最一般的包含 V 的代数，而且其乘法是在 V 上交替的，很自然可以从包含 V 的最一般的代数开始，也就是张量代数T(V)，然后通过合适的商来强制交替的性质。这样我们取 T(V) 中由所有形为 v⊗v的元素生成的双边理想I，其中 v 属于 V，并定义 Λ(V)为商

（并且使用 ∧ 为 Λ(V)中的乘法的代号）。然后可以直接证明 Λ(V) 包含 V 并且满足上述泛性质。

如果不是先定义 Λ(V) 然后把外幂 Λ(V) 等同为特定的子空间，我们也可以先定义空间 Λ(V) 然后把它们合并成为一个代数 Λ(V)。这个方法在微分集合中常常用到，并在下节中有描述。

反对称算子和外幂

给定两个向量空间V和X，一个从V到X的反对称算子是一个多线性映射

使得只要v1,...,vk 是V中线性相关的向量，则

最著名的例子是行列式值，从(K)到K的反对称线形算子。

映射

它关联V中的k个向量到他们的楔积，也就是它们相应的k-向量，这也是反对称的。事实上，这个映射是定义在V上的“最一般”的反对称算子：给定任何其它反对称算子f : V → X，存在一个唯一的线性映射φ: Λ(V) → X with f = φ o w。这个泛性质表述了空间Λ(V)并且可以作为它的定义。

所有从V到基域K的反对称映射组成一个向量空间，因为两个这样的映射的和、或者这样一个映射和一个标量的乘积也是反对称的。若V是有限维的，维数n，则该空间可以认同为Λ(V)，其中V表示V的对偶空间。特别的有，从V到K的反对称映射的空间是n取k维的。

在这个等同关系下，若基域是R或者C，楔积有一个具体的形式：它从两个给定的反对称映射得到一个新的反对称映射。设ω : V → K和η : V → K为两个反对称映射。和在多线性映射的张量积的情况一样，楔积的变量数是每个映射的变量数之和。它定义如下：

其中多线性映射的交替Alt定义为其变量的所有排列的带符号平均：

注意： 有一些书中楔积定义为

指标记法

在主要由物理学家使用的指标记法中

微分形式

令 M 为一个微分流形。一个微分k-形式ω 是 ΛTM（M 的余切丛的 k 阶外幂）的一个截面。等价的有：ω 是 M 的光滑函数，对于 M 的每个点 x 给定一个 Λ(TxM)的元素。大致来讲，微分形式是余切向量的全局版本。微分形式是微分几何的重要工具，其中，它们被用于定义德拉姆上同调和亚历山大-斯潘尼尔上同调。

推广

给定一个交换环R和一个R-模M，我们可以定义和上文一样的外代数Λ(M)，它是张量代数T(M)适当的商。它会满足类似的泛性质。

物理应用

格拉斯曼代数在物理中有重要应用，它们被用于建模和费米子和超对称性相关的各种概念。

参看：超空间，超代数，超群

注释

^R. Penrose. The Road to Reality. Vintage books. 2007. ISBN 0-679-77631-1. 

^J.A. Wheeler, C. Misner, K.S. Thorne. Gravitation. W.H. Freeman & Co. 1973: 83. ISBN 0-7167-0344-0. 

^由下述等价关系∼ ∼ -->{\displaystyle \sim } 所形成的等价类：∀ ∀ -->u,v∈ ∈ -->T(V),u∼ ∼ -->v⇔ ⇔ -->u− − -->v∈ ∈ -->I.{\displaystyle \forall u,v\in T(V)\,,u\sim v\Leftrightarrow u-v\in I\,.}

相关课题

多线性代数

张量代数

对称代数

克利福德代数

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。