怎样区分粒子

有两种方法可以用来区分粒子。第一种方法倚靠粒子所具有的不同的物理性质，像质量、电荷、自旋等等，假若粒子的性质有任何的不同，则可以借着测量这不同的性质来区分粒子。根据做实验获得的结果，同一种类的粒子都具有完全相同的物理性质，例如，宇宙里所有的电子都拥有同样的电荷。这就是为什么在论述时经常会提到电子的电荷，而不是哪一个电子的电荷。

第二种区分法跟踪每一个粒子的轨道。只要能够无限精确地测量出每一个粒子的位置，就不会搞不清楚哪一个粒子在哪里。这个方法有一个问题，那就是它与量子力学的基本原理相矛盾。根据量子理论，在位置测量期间，粒子并不会保持明确的位置。粒子的位置是由波函数来决定。而波函数只能给予粒子在每一个位置的概率。随着时间演变，几个粒子的波函数会扩散蔓延，互相重叠。一但重叠事件发生，就无法区分在重叠区域的两个粒子。这样，粒子就越来越不可区分了。

量子力学的描述

对称与反对称量子态

应用量子力学的数学表述条目里的形式论，来做更具体的讲述，为了简易起见，设想一个量子系统，内中有两个全同粒子。因为这两个粒子具有完全相同的物理性质，它们的态矢量的希尔伯特空间完全相同。假若标记一个粒子的希尔伯特空间为 H{\displaystyle H\,\!} ，则这两个粒子结合的希尔伯特空间是张量乘积H⊗ ⊗ -->H{\displaystyle H\otimes H\,\!} 。

设定 n{\displaystyle n\,\!} 来标记单独粒子量子态的（离散的）量子数（例如，在盒中粒子问题里，设定 n{\displaystyle n\,\!} 为波函数的量子化的波数）。假设一个粒子处于量子态 |n1⟩ ⟩ -->{\displaystyle |n_{1}\rangle \,\!} ，另一个粒子处于量子态 |n2⟩ ⟩ -->{\displaystyle |n_{2}\rangle \,\!} 。那么，什么是结合系统的量子态？或许猜想答案是

这只是一个正则方法，从单独空间之结合，建构出一个张量乘积空间的基底。设定这表达式的第一个量子态为粒子 1 的量子态，第二个量子态为粒子 2 的量子态。那么，这个表达式意味着可以区分粒子 1 是量子数为 n1{\displaystyle n_{1}\,\!} 的粒子，粒子 2 是量子数为 n2{\displaystyle n_{2}\,\!} 的粒子的粒子。可是，量子数不是粒子的内在物理性质。不能做这样的区分。

事实上，实验的结果显示出，全同粒子的量子态是特别种类的多粒子量子态，称为对称态或反对称态。对称态的形式为

反对称态的形式为

其中，等价方程左手边的两个参数是允许的量子数。S{\displaystyle S\,\!} 代表对称态 (symmetric state) ，A{\displaystyle A\,\!} 代表反对称态 (antisymmetric state) ；右手边的括弧内每一个项目的第一个量子态是粒子 1 的量子态，第二个量子态是粒子 2 的量子态。两个量子态的前后顺序很重要：

注意到假若 n1{\displaystyle n_{1}\,\!} 等于 n2{\displaystyle n_{2}\,\!} ，则反对称态会给出 0 。这概率幅是实际物理所不允许的。所以，反对称态的两个全同粒子不能处于同样的量子态。这规则就是著名的泡利不相容原理，是造成原子千变万化的化学性质的主要因素。

交换对称性

对称态与反对称态的概念的正确性，最终是建立于实验获得的证据。大自然似乎并不允许全同粒子的量子态具有混合的对称性，像下述公式：

事实上，这个规则有一个例外，稍后，会对这例外有所说明。从另外一方面来看，可以表明对称态与反对称态，就某种意义来说，是很特别的。检视多粒子量子态的一种特别的对称性，称为交换对称性。

定义一个线性算符P{\displaystyle P\,\!} ，称为交换算符。当交换算符作用于量子系统的两个粒子时，这两个粒子会互相交换：

原来粒子 1 的量子态是 |ψ ψ -->⟩ ⟩ -->{\displaystyle |\psi \rangle \,\!} ，粒子 2 的量子态是 |ϕ ϕ -->⟩ ⟩ -->{\displaystyle |\phi \rangle \,\!} 。经过 P{\displaystyle P\,\!} 作用后，粒子 1 与粒子 2 交换。所以粒子 1 的量子态变为 |ϕ ϕ -->⟩ ⟩ -->{\displaystyle |\phi \rangle \,\!} ，而粒子 2 的量子态变为 |ψ ψ -->⟩ ⟩ -->{\displaystyle |\psi \rangle \,\!} 。

算符 P{\displaystyle P\,\!} 是个厄米算符和幺正算符。因为它是幺正的，可以将它视为一个对称性算符，可以描述这个对称性为粒子量子态的交换对称性：经过 P{\displaystyle P\,\!} 作用后，粒子 1 的量子态与粒子 2 的量子态交换。

明确地，P2=1{\displaystyle P^{2}={\boldsymbol {1}}\,\!} （ 1{\displaystyle {\boldsymbol {1}}\,\!} 是单位算符）。所以，P{\displaystyle P\,\!} 的本征值为 +1{\displaystyle +1\,\!} 或 − − -->1{\displaystyle -1\,\!} 。对应的本征态是对称态与反对称态：

注意到，经过粒子的交换，对称态与反对称态基本上并无改变，它们只被乘以一个因子 +1{\displaystyle +1\,\!} 或 − − -->1{\displaystyle -1\,\!} ，而不是被希伯于希伯尔特空间。这证明了粒子的标签并无任何物理意义，这与前面关于不可区分的讲述相符合。

由于 P{\displaystyle P\,\!} 是个厄米算符，它是一个可观察量。理论上，可以做一个实验测量来查明它到底是对称态，还是反对称态。此外，粒子的全同意味着哈密顿量可以写为对称形式，像

很明显地，交换算符与哈密顿量满足正则对易关系

根据海森堡绘景，这方程表明 P{\displaystyle P\,\!} 是个运动常数。假若一个量子态本来是对称态（反对称态），随着时间的演变，它仍旧会是对称态（反对称态）。在数学里，态矢量被限制为 P{\displaystyle P\,\!} 的两个本征态之中的一个；它无法以整个希伯尔特空间为值域范围。因此，可以干脆将本征空间当为这系统的真正的希伯尔特空间。这就是佛克空间 (Fock space) 的定义背后的点子。

费米子与玻色子

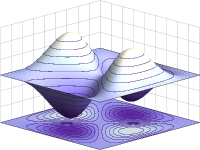
在无限深方形阱里，两个全同费米子的反对称性波函数绘图。

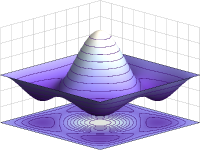
在无限深方形阱里，两个全同玻色子的对称波函数绘图。

粒子的种类决定了它们的量子态是对称态或反对称态。例如，当描述光子、氦-4 原子时，必须用到对称态；而当描述电子、质子时，就必须用到反对称态。

量子态是对称态的粒子称为玻色子。稍后会说明，对于一个许多全同玻色子组成的系统，对称性给予了非常重要的统计性质。这些统计性质称为玻色-爱因斯坦统计。

量子态是反对称态的粒子称为费米子。反对称性造成了泡利不相容原理的产生，使得全同费米子被禁止共处于同样的量子态。费米-狄拉克统计专门描述许多全同费米子组成的系统，

在某些二维系统里，混合对称性也可能发生。这些奇特的粒子被称为任意子(anyon) 。它们遵守分数统计 (fractional statistics)。分数量子霍尔效应实验的证明了任意子的存在。在形成MOSFET反转层的二维电子气体里，也观察到了这种效应。另外有一种统计，称为辫统计 (braid statistics) ，是用来描述许多全同普瑞顿子 (plekton) 组成的系统，

自旋统计理论将全同粒子的交换对称性追溯至它们的自旋。这理论阐明玻色子的自旋是正整数，费米子的自旋是半整数，任意子的自旋是分数。

N 个粒子

前面的讲述可以很容易地推广至 N{\displaystyle N\,\!} 个粒子的案例。设定 N{\displaystyle N\,\!} 个粒子。再设定 N{\displaystyle N\,\!} 个量子数为 ni{\displaystyle n_{i}\,\!} 的单独粒子量子态 |ni⟩ ⟩ -->,1≤ ≤ -->i≤ ≤ -->N{\displaystyle |n_{i}\rangle ,\quad 1\leq i\leq N\,\!} 。设定其中独特的量子数为 η η -->1,η η -->2,… … -->,η η -->L,L≤ ≤ -->N{\displaystyle \eta _{1},\,\eta _{2},\,\dots ,\,\eta _{L},\quad L\leq N\,\!} 。Nj{\displaystyle N_{j}\,\!} 代表量子数 η η -->j{\displaystyle \eta _{j}\,\!} 出现的次数（简并度）。

假若这些粒子都是玻色子，则描述它们的量子态是完全对称态，对于任何两个粒子的交换，都是对称的：

其中， permutation(N){\displaystyle \mathrm {permutation} (N)\,\!} 代表所有从整数 1{\displaystyle 1\,\!} 到 N{\displaystyle N\,\!} 的置换的集合。这集合里面有 N!{\displaystyle N!\,\!} 个元素。因此，公式右边的总合表达式一共有 N!{\displaystyle N!\,\!} 项目，每一个项目的指数 p{\displaystyle p\,\!} 是置换集合 permutation(N){\displaystyle \mathrm {permutation} (N)\,\!} 的一个元素。指数 p{\displaystyle p\,\!} 内部第 i{\displaystyle i\,\!} 个字位 pi{\displaystyle p_{i}\,\!} 所代表的整数指定粒子 i{\displaystyle i\,\!} 的量子数 npi{\displaystyle n_{p_{i}}\,\!} 。平方根系数是一个归一化常数。

假若这些粒子都是费米子，则描述它们的量子态是完全反对称态，对于任何两个粒子的交换，都是反对称的：

其中，sign(p){\displaystyle \mathrm {sign} (p)\,\!} 是正号或负号。假若元素 p{\displaystyle p\,\!} 属于偶置换，则是正号；否则即是负号。注意到在这里并没有 ∏ ∏ -->jNj!{\displaystyle \prod _{j}N_{j}!\,\!} 这个总乘积项目，因为每一个单独粒子量子态只能出现一次；否则，概率幅等于 0{\displaystyle 0\,\!} 。

这些多粒子量子态方程都已经归一化：

斯莱特行列式

用位置空间的波函数来表示，标记 N{\displaystyle N\,\!} 个费米子的波函数为 Ψ Ψ -->n1⋯ ⋯ -->nN(A)(x1,⋯ ⋯ -->xN){\displaystyle \Psi _{n_{1}\cdots n_{N}}^{(A)}(x_{1},\cdots x_{N})\,\!} ；其中，n1⋯ ⋯ -->nN{\displaystyle n_{1}\cdots n_{N}\,\!} 是允许的量子数，波函数的第 i{\displaystyle i\,\!} 个参数 xi{\displaystyle x_{i}\,\!} 是粒子 i{\displaystyle i\,\!} 的位置。将量子数是 ni{\displaystyle n_{i}\,\!} 的单独粒子波函数标记为 ψ ψ -->ni{\displaystyle \psi _{n_{i}}\,\!} 。单独粒子波函数只有一个位置参数 x{\displaystyle x\,\!} 。这样，N{\displaystyle N\,\!} 个费米子的波函数可以用斯莱特行列式表示

范例

二个全同玻色子

三个全同玻色子

二个全同费米子

三个全同费米子

统计性质

在统计行为上，玻色子与费米子有很重要的差别。玻色子的统计行为是以玻色-爱因斯坦统计来描述，费米子的统计行为则是以费米-狄拉克统计来描述。粗略地说，玻色子喜好凝聚于同样的量子态。因此，造成了激光、玻色-爱因斯坦凝聚、超流体等等量子现象。在另一方面，费米子禁止共同享有同样的量子态，造成了像费米气体、白矮星、中子星等等奇异的系统。这规则称为泡利不相容原理。大多数的化学现象都与这原理有关。在原子里，因为这原理，电子依次地装填一层一层的电子层，而不是全部处于最低能量的量子态。

可区分粒子，玻色子，与费米子在统计行为上有很大的不同。称两个粒子为 A{\displaystyle A\,\!} 和 B{\displaystyle B\,\!} 。每一个粒子都可以处于两个能量相同的量子态，|0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} 与 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 。

假若 A{\displaystyle A\,\!} 和 B{\displaystyle B\,\!} 是可区分粒子，则可能有四种不同的量子态：

|0⟩ ⟩ -->|0⟩ ⟩ -->{\displaystyle |0\rangle |0\rangle \,\!} ，

|1⟩ ⟩ -->|1⟩ ⟩ -->{\displaystyle |1\rangle |1\rangle \,\!} ，

|0⟩ ⟩ -->|1⟩ ⟩ -->{\displaystyle |0\rangle |1\rangle \,\!} ，

|1⟩ ⟩ -->|0⟩ ⟩ -->{\displaystyle |1\rangle |0\rangle \,\!} 。

统计力学的基础假设阐明：给予一个处于热力平衡的隔离系统，则每一个能量相同的微观状态都有相同的概率成为系统的状态。根据这基础假设，两个粒子都处于 |0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} 的概率是 0.25{\displaystyle 0.25\,\!} ，两个粒子都处于 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 的概率是 0.25{\displaystyle 0.25\,\!} ，而一个粒子处于 |0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} ，另一个粒子处于 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 的概率是 0.5{\displaystyle 0.5\,\!} 。

假若 A{\displaystyle A\,\!} 和 B{\displaystyle B\,\!} 是全同玻色子，则可能有三种不同的量子态：

|0⟩ ⟩ -->|0⟩ ⟩ -->{\displaystyle |0\rangle |0\rangle \,\!} ，

|1⟩ ⟩ -->|1⟩ ⟩ -->{\displaystyle |1\rangle |1\rangle \,\!} ，

12(|0⟩ ⟩ -->|1⟩ ⟩ -->+|1⟩ ⟩ -->|0⟩ ⟩ -->){\displaystyle {\frac {1}{\sqrt {2}}}(|0\rangle |1\rangle +|1\rangle |0\rangle )\,\!} 。

假若这个隔离系统正处于热力平衡，则两个粒子都都处于 |0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} 的概率是 0.33{\displaystyle 0.33\,\!} ，两个粒子都都处于 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 的概率也是 0.33{\displaystyle 0.33\,\!} ，而一个粒子处于 |0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} ，另一个粒子处于 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 的概率还是 0.33{\displaystyle 0.33\,\!} 。请注意，找到玻色子处于同样的量子态的概率大于可区分粒子处于同样的量子态的概率。这表明了玻色子的趋向于凝聚。

假若 A{\displaystyle A\,\!} 和 B{\displaystyle B\,\!} 是全同费米子，则只有一种可能的量子态：

当做测量实验时，会必然地得到一个粒子处于 |0⟩ ⟩ -->{\displaystyle |0\rangle \,\!} ，另一个粒子处于 |1⟩ ⟩ -->{\displaystyle |1\rangle \,\!} 。

桌表 1 展示出前面讲述的结果：

参阅

盒中气体

麦克斯韦-玻兹曼统计

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。