一般用法

交换律 是一个和二元运算及函数有关的性质。而若交换律对一特定二元运算下的一对元素成立，则称这两个元素为在此运算下是“可交换”的。

在群论和集合论中，许多的代数结构被称做是可交换的，若其中的运算域满换律。在数学分析和线性代数中，一些知名的运算（如实数及复数上的加法和乘法）的交换律会经常被用于（或假定存在于）证明之中。

数学定义

“可交换”一词被使用于如下几个相关的概念中 ：

1. 在集合 S 的一二元运算* 被称之为“可交换”的，若：

一个不满足上述性质的运算则称之为“不可交换”的。

2. 若称 x 在 * 下和 y “可交换”，即表示：

3. 一二元函数 f: A × A → B 被称之为“可交换”的，若：

历史

  对这一词第一个已知的应用是在1814年的一本法国期刊上

对交换律假定存在的应用早在很久之前便已有所记戴。埃及人用乘法的交换律来简化乘积的计算。 且知欧几里得在《几何原本》中已有假定了乘法交换律的存在。 对交换律形式上的应用产生于18世纪末19世纪初，那时数学家开始在研究函数的理论。今日，交换律已被普遍认知，且在大多数的数学分支中被当做基本性质来使用。交换律的简易版本通常会在初等数学教程中被教导。

第一个使用“可交换（commutative）”一词的是 Francois Servois 于1814年写下的笔记 ，这一词在笔记中被用来指有着现在称之为交换律的函数。这一词首次出现于英语中的是在1844年的英国皇家学会哲学汇刊中。

相关性质

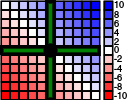
  显示加法函数对称性的图

结合律

结合律和交换律密切相关着。结合律是指运算的顺序并不会影响其最终结果。相对地，交换律则是指算子的顺序不会影响其最终结果的性质。

对称

对称可以和交换律有直接的关连。若将一个可交换运算子写成一个二元函数，则此一函数会对 y = x 这条线对称。举例来说，若设一函数 f 来表示加法（一可交换运算），所以 f ( x , y ) = x + y ，也因此 f 会是个如右图所见的对称函数。

例子

日常生活中的可交换运算

洗一双鞋子可类比为一可交换运算，因为不论是左边的鞋子先洗，还是右边的鞋子先洗，最终的结果（两只鞋子都洗好）是一样的。

成语“朝三暮四”也可看做是可交换运算的一个例子。

数学中的可交换运算

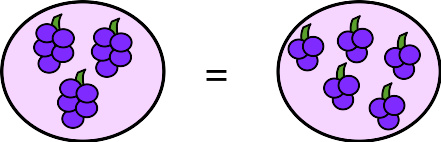
  显现出乘法 ( 5* 3 = 3 * 5 ) 的交换律的一个例子

两个广为人知的可交换二元运算的例子为 ：

实数的加法

实数的乘法

更多可交换二元运算的例子包括复数的乘法、向量的加法、和集合的交集与并集。

日常生活中的不可交换运算

 串接（将字串连在一起的行为）是个不可交换运算。

洗衣和干衣可类比成不可交换运算，因为先干衣再洗衣和先洗衣再干衣两者会得出很不同的结果来。

魔术方块是不可交换的。例如，将正面顺时针扭转，顶面顺时针扭转，再将正面逆时针扭转（FUF"），并不会得出如将正面顺时针扭转，再将正面逆时针扭转，最后再将顶面顺时针扭转（FF"U）一样的结果。扭转是不可交换的。这些扭转被研究于群论中。

数学中的不可交换运算

一些不可交换二元运算 有：

减法： 0 − − --> 1 ≠ ≠ --> 1 − − --> 0 {\displaystyle 0-1\neq 1-0} 不过可将其减法符号转换成加上其相反数，即可使用交换律。

除法： 1 ÷ ÷ --> 2 ≠ ≠ --> 2 ÷ ÷ --> 1 {\displaystyle 1\div 2\neq 2\div 1} 可将除法转换成乘上其倒数以使用交换律。

矩阵乘法：

数学结构与交换律

阿贝尔群是一个群运算为可交换的群。

交换环是一个乘法为可交换的环。（环中的加法依定义总会是可交换的。）

域的加法与乘法都是可交换的。

中心是一个群最大的可交换子集。

参考资料

书籍

Axler, Sheldon. Linear Algebra Done Right, 2e. Springer. 1997. ISBN 978-0-387-98258-8.

Goodman, Frederick. Algebra: Abstract and Concrete, Stressing Symmetry, 2e. Prentice Hall. 2003. ISBN 978-0-13-067342-8.

Gallian, Joseph. Contemporary Abstract Algebra, 6e. 2006. ISBN 978-0-618-51471-7.

文章

http://www.ethnomath.org/resources/lumpkin1997.pdfLumpkin, B. (1997). The Mathematical Legacy Of Ancient Egypt - A Response To Robert Palter. Unpublished manuscript.

Robins, R. Gay, and Charles C. D. Shute. 1987. The Rhind Mathematical Papyrus: An Ancient Egyptian Text . London: British Museum Publications Limited. ISBN 978-0-7141-0944-2

线上资源

Krowne, Aaron, Commutative atPlanetMath., Accessed 8 August 2007.

MathWorld上 Commute 的资料，作者：埃里克·韦斯坦因。, Accessed 8 August 2007.

Yark. Examples of non-commutative operations atPlanetMath., Accessed 8 August 2007

O"Conner, J J and Robertson, E F.MacTutor history of real numbers, Accessed 8 August 2007

Cabillón, Julio and Miller, Jeff.Earliest Known Uses Of Mathematical Terms, Accessed 8 August 2007

O"Conner, J J and Robertson, E F.MacTutor biography of François Servois, Accessed 8 August 2007

另见

反交换律

二元运算

交换子集合

交换子

分配律

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。