向量与积分

共形映射作用于矩形网格。注意，弯曲的网格的正交性被保留。

用数学术语，正交坐标的度规张量绝对没有非对角项目。换句话说，无穷小距离的平方 d s 2 {\displaystyle ds^{2}} ，可以写为无穷小坐标位移的平方和：

其中， n {\displaystyle n} 是维数，标度因子 h i {\displaystyle h_{i}} 是度规张量的对角元素 g i i {\displaystyle g_{ii}} 的平方根：

这些标度因子可以用来计算一个正交坐标系的微分算子。例如，梯度、拉普拉斯算子、散度、或旋度。

从前面的距离公式，可以观察出，一个正交坐标 q i {\displaystyle q_{i}} 的无穷小改变 d q i {\displaystyle dq_{i}} ，其相伴的长度是 d s i = h i d q i {\displaystyle ds_{i}=h_{i}dq_{i}} 。因此，一个位移向量的全微分 d r {\displaystyle d\mathbf {r} } 等于

其中， e i {\displaystyle \mathbf {e} _{i}} 是垂直于 q i {\displaystyle q_{i}} 等值曲面的单位向量，指向着 q i {\displaystyle q_{i}} 增值最快的方向，这些单位向量形成了一个局部直角坐标系的坐标轴。

在正交坐标系里，内积的公式仍旧不变：

因此，向量 F {\displaystyle \mathbf {F} } 沿着周线 C {\displaystyle \mathbb {C} } 的线积分等于

其中， F i {\displaystyle F_{i}} 是向量 F {\displaystyle \mathbf {F} } 在单位向量 e i {\displaystyle \mathbf {e} _{i}} 方向的分量：

类似地，一个无穷小面积元素是

一个无穷小体积元素是

例如，向量 F {\displaystyle \mathbf {F} } 对于一个曲面 S {\displaystyle \mathbb {S} } 的曲面积分是

球坐标系实例

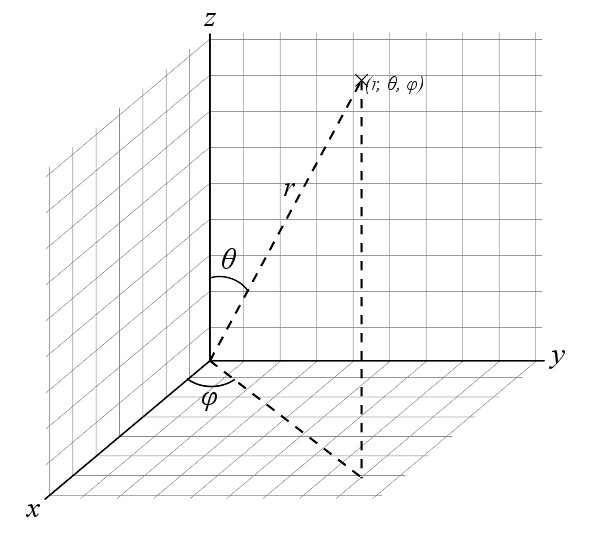
球坐标系内的一点与它的球坐标。

直角坐标 ( x , y , z ) {\displaystyle (x,\ y,\ z)} 与球坐标 ( r , θ θ --> , ϕ ϕ --> ) {\displaystyle (r,\ \theta ,\phi )} 的变换方程式为

直角坐标的全微分是

所以，无穷小距离的平方是

标度因子是

向量 F {\displaystyle \mathbf {F} } 沿着周线 C {\displaystyle \mathbb {C} } 的线积分等于

向量 F {\displaystyle \mathbf {F} } 对于一个曲面 S {\displaystyle \mathbb {S} } 的曲面积分是

三维微分算子

梯度导引

一个函数 ϕ ϕ --> {\displaystyle \phi } 的梯度朝某个方向 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 的分量，等于方向导数 d ϕ ϕ --> d s {\displaystyle {\frac {d\phi }{ds}}} 朝 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 方向的值：

其中， d s {\displaystyle ds} 是朝 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 方向的无穷小位移。

假若，这 n ^ ^ --> {\displaystyle {\hat {\mathbf {n} }}} 与正交坐标轴 e ^ ^ --> i {\displaystyle {\hat {\mathbf {e} }}_{i}} 同方向。那么， d s = h i d q i {\displaystyle ds=h_{i}dq_{i}} 。所以，函数 ϕ ϕ --> {\displaystyle \phi } 的梯度朝 e ^ ^ --> i {\displaystyle {\hat {\mathbf {e} }}_{i}} 的分量是 ∂ ∂ --> ϕ ϕ --> h i ∂ ∂ --> q i {\displaystyle {\frac {\partial \phi }{h_{i}\partial q_{i}}}} ；也就是说，

散度导引

取右手边第一个项目，

应用向量恒等式 ∇ ∇ --> ⋅ ⋅ --> ( A ϕ ϕ --> ) = ϕ ϕ --> ∇ ∇ --> ⋅ ⋅ --> A + A ⋅ ⋅ --> ( ∇ ∇ --> ϕ ϕ --> ) {\displaystyle \nabla \cdot (\mathbf {A} \phi )=\phi \nabla \cdot \mathbf {A} +\mathbf {A} \cdot (\nabla \phi )} 与 ∇ ∇ --> ⋅ ⋅ --> ( ∇ ∇ --> ϕ ϕ --> 1 × × --> ∇ ∇ --> ϕ ϕ --> 2 ) = 0 {\displaystyle \nabla \cdot (\nabla \phi _{1}\times \nabla \phi _{2})=0} ，可以得到

总合所有项目，

旋度导引

取右手边第一个项目，

应用向量恒等式 ∇ ∇ --> × × --> ( A ϕ ϕ --> ) = ϕ ϕ --> ∇ ∇ --> × × --> A − − --> A × × --> ( ∇ ∇ --> ϕ ϕ --> ) {\displaystyle \nabla \times (\mathbf {A} \phi )=\phi \nabla \times \mathbf {A} -\mathbf {A} \times (\nabla \phi )} ，

应用向量恒等式 ∇ ∇ --> × × --> ( ∇ ∇ --> ϕ ϕ --> ) = 0 {\displaystyle \nabla \times (\nabla \phi )=0} ，

总合所有项目，

拉普拉斯算子

参考文献

Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers , McGraw-Hill, pp. 164-182。

Morse PM and Feshbach H. (1953) Methods of Theoretical Physics , McGraw-Hill, pp. 494-523, 655-666。

Margenau H. and Murphy GM. (1956) The Mathematics of Physics and Chemistry , 2nd. ed., Van Nostrand, pp. 172-192。

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。