示例

等边三角形

正方形

正五边形

正六边形

正八边形

正十边形

正十二边形

特性

正 n 边形每个内角为 ( 1 − − --> 2 n ) × × --> 180 ∘ ∘ --> {\displaystyle \left(1-{\frac {2}{n}}\right)\times 180^{\circ }} 或者表示为 ( n − − --> 2 ) × × --> 180 ∘ ∘ --> n {\displaystyle {\frac {(n-2)\times 180^{\ci弧度 }}{n}}} 角度。也可以用弧度表示为 ( n − − --> 2 ) π π --> n {\displaystyle {\frac {(n-2)\pi }{n}}} 或者 n − − --> 2 2 n {\displaystyle {\frac {n-2}{2n}}} 。

正多边形的所有顶点都在同一个外接圆上，每个正多边形都有一个外接圆。

正多边形可尺规做图当且仅当正多边形的边数 n 的奇质数因子是费马数。参见可尺规作图的多边形。

n > 2 的正多对角线对角线数目是 n ( n − − --> 3 ) 2 {\displaystyle {\frac {n(n-3)}{2}}} ，如 0、2、5、9、... 等，这些对角线将多边形分成 1、4、 11、24、... 块。

面积

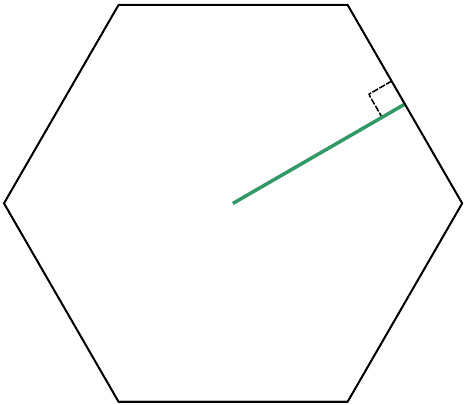
正六边形的垂直边心距

正 n 边形的面积为

其中 t 是边长。正多边形的面积还等于多边形的周长与边心距离乘积的一半。边心距离是多边形中心到边的垂直距离。

如果 t =1 则正多边形的面积为,

从而可以得到

n<8 的正多边形的面周长同周长的圆的面积小大约 0.26，随着 n 的增加，这个差值趋近于 π/12。

对称性

n 边多边形的对称群 为 2 n 阶的 dihedral group D n ： D 2 , D 3 , D 4 ,... 它包括 C n 中的 n 阶旋转对称以及经过中心的 n 条轴线的镜像对称。如果 n 是偶数，则这些轴线中有一半经过相对的顶点，另外一半经过相对边的中点。如果 n 是奇数，则所有的轴线都是经过一个顶点以及其相对边的中心。

非凸正多边形

正多边形的广义分类包括星形多边形，例如五角星与五边形的顶点相同，但是顶点要交替相连。

示例：

五角星- {5/2}

七角星- {7/2}, {7/3}

八角星- {8/3}

九角星- {9/2}, {9/4}

十角星- {10/3}

多面体

正多面体是以正多边形作为面的多面体，因此对于每两个顶点来说都有一个等距的映射将其中一点映射到另一点。

参见

正多边形镶嵌

外接圆

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。