开普勒定律

开普勒的三条行星运动定律改变了整个天文学，彻底摧毁了托勒密复杂的宇宙体系，完善并简化了哥白尼的日心说。

开普勒第一定律

根据开普勒第一定律，太阳位于椭圆轨道的一个焦点。

开普勒第一定律，也称椭圆定律、轨道定律：每一个行星都沿各自的椭圆轨道环绕太阳，而太阳则处在椭圆的一个焦点中。

开普勒第二定律

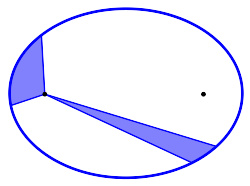
根据开普勒第二定律，在同样时间间隔内，行星绕着太阳公转所扫过的面积相等。

开普勒第二定律，也称等面积定律：在相等时间内，太阳和运动着的行星的连线所扫过的面积都是相等的。

这一定律实际揭示了行星绕太阳公转的角动量守恒。用公式表示为

开普勒第三定律

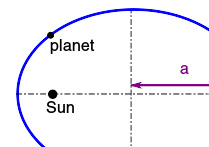
根据开普勒第三定律，行星绕着太阳公转的周期平方和它们的椭圆轨道的半长轴立方成正比。

开普勒第三定律，也称周期定律：各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。

由这一定律不难导出：行星与太阳之间的引力与半径的平方成反比。这是艾萨克·牛顿的万有引力定律的一个重要基础。

用公式表示为

这里，a{\displaystyle a} 是行星公转轨道半长轴，τ τ -->{\displaystyle \tau } 是行星公转周期，K{\displaystyle K} 是常数。

数学推导：由牛顿万有引力定律导出开普勒定律

开普勒定律描述的是行星围绕太阳的运动，牛顿定律可以更广义地描述几个粒子因万有引力相互吸引而形成的运动。假设只有两个粒子，其中一个粒子超轻于另外一个粒子，则轻的粒子会绕着重的粒子运动，就好似行星根据开普勒定律绕著太阳运动。另外，牛顿定律还可计算出关于其它方面的解答，行星轨道可以呈抛物线运动或双曲线运动。这是开普勒定律所无法预测到的结果。在一个粒子并不超轻于另外一个粒子的状况下，依照广义二体问题的解答，每一个粒子会绕着它们的共同质心运动。这也是开普勒定律无法预测到的。

开普勒定律使用几何语言将行星的坐标及时间跟轨道参数相连结。牛顿第二定律是一个微分方程。开普勒定律的推导涉及一些解析微分方程的技巧。在推导开普勒第一定律之前，必须先推导出开普勒第二定律，因为开普勒第一定律需要用到开普勒第二定律里的一些计算结果。

开普勒第二定律推导

牛顿万有引力定律表明，任意两个粒子由通过连线方向的力相互吸引。该引力的的大小与它们的质量乘积成正比，与它们距离的平方成反比。由于太阳超重于行星，可以假设太阳是固定的。用方程表示，

这里，F{\displaystyle {\boldsymbol {F}}} 是太阳作用于行星的万有引力，m{\displaystyle m} 是行星的质量，M{\displaystyle M} 是太阳的质量，r{\displaystyle {\boldsymbol {r}}} 是行星相对于太阳的位移矢量，r^ ^ -->{\displaystyle {\hat {\boldsymbol {r}}}} 是 r{\displaystyle {\boldsymbol {r}}} 的单位矢量。

牛顿第二定律表明，物体受力后所产生的加速度r¨ ¨ -->{\displaystyle {\ddot {\boldsymbol {r}}}} ，和其所受的合力 F{\displaystyle {\boldsymbol {F}}} 成正比，和其质量 m{\displaystyle m} 成反比，以方程表示，

合并这两个方程，

思考位置矢量 r=rr^ ^ -->{\displaystyle {\boldsymbol {r}}=r{\hat {\boldsymbol {r}}}} ，对于时间 t{\displaystyle t} 微分一次可得到速度矢量，再微分一次则可得到加速度矢量：

在这里，用到了单位矢量微分方程：

合并方程 (1) 与 (2) ，可以得到矢量运动方程：

取各个分量，可以得到两个常微分方程，一个是关于径向加速度，另一个是关于切向加速度：

导引开普勒第二定律只需切向加速度方程。试想行星的角动量ℓ ℓ -->=mr2θ θ -->˙ ˙ -->{\displaystyle \ell =mr^{2}{\dot {\theta }}} 。由于行星的质量是常数，角动量对于时间的导数为

角动量 ℓ ℓ -->{\displaystyle \ell } 也是一个运动常数，即使距离 r{\displaystyle r} 与角速度 θ θ -->˙ ˙ -->{\displaystyle {\dot {\theta }}} 都可能会随时间变化。

从时间 t1{\displaystyle t_{1}} 到时间 t2{\displaystyle t_{2}} 扫过的区域 Δ Δ -->A{\displaystyle \Delta A} ，

行星太阳连线扫过的区域面积相依于间隔时间 t2− − -->t1{\displaystyle t_{2}-t_{1}} 。所以，开普勒第二定律是正确的。

开普勒第一定律推导

设定 u=1r{\displaystyle u={\frac {1}{r}}} 。这样，角速度是

对时间微分和对角度微分有如下关系：

根据上述关系，径向距离 r=1u{\displaystyle r={\frac {1}{u}}} 对时间的导数为：

再求一次导数：

代入径向运动方程 (3) ，r¨ ¨ -->− − -->rθ θ -->˙ ˙ -->2=− − -->GMr2{\displaystyle {\ddot {r}}-r{\dot {\theta }}^{2}=-{\frac {GM}{r^{2}}}} ，

将此方程除以 − − -->ℓ ℓ -->2u2m2{\displaystyle -{\frac {\ell ^{2}u^{2}}{m^{2}}}} ，则可得到一个简单的常系数非齐次线性全微分方程来描述行星轨道：

为了解这个微分方程，先列出一个特解

再求解剩余的常系数齐次线性全微分方程，

它的解为

这里，C{\displaystyle C} 与 θ θ -->0{\displaystyle \theta _{0}} 是常数。合并特解和与齐次方程解，可以得到通解

选择坐标轴，让 θ θ -->0=0{\displaystyle \theta _{0}=0} 。代回 u=1r{\displaystyle u={\frac {1}{r}}} ，

其中，e=Cℓ ℓ -->2/GMm2{\displaystyle e=C\ell ^{2}/GMm^{2}离心率离心率。

这是圆锥曲线的极坐标方程，坐标系的原点是圆锥曲线的焦点之一。假若 0<e<1{\displaystyle 0 ，则 r{\displaystyle r} 所描述的是椭圆轨道。这证明了开普勒第一定律。

开普勒第三定律推导

在建立牛顿万有引力定律的概念与数学架构上，开普勒第三定律是牛顿依据的重要线索之一。假若接受牛顿运动定律。试想一个虚拟行星环绕着太阳公转，行星的移动轨道恰巧呈圆形，轨道半径为 r{\displaystyle r} 。那么，太阳作用于行星的万有引力为 F=mv2r{\displaystyle F={\frac {mv^{2}}{r}}} 。行星移动速度为 v=2π π -->rτ τ -->{\displaystyle v={\frac {2\pi r}{\tau }}} 。依照开普勒第三定律，这速度 v{\displaystyle v} 与半径的平方根 r{\displaystyle {\sqrt {r}}} 成反比。所以，万有引力 F∝ ∝ -->1r2{\displaystyle F\propto {\frac {1}{r^{2}}}} 。猜想这大概是牛顿发现万有引力定律的思路，但这个猜想无法被证实，因为在他的计算本里，并没有找到任何关于这方面的证据。

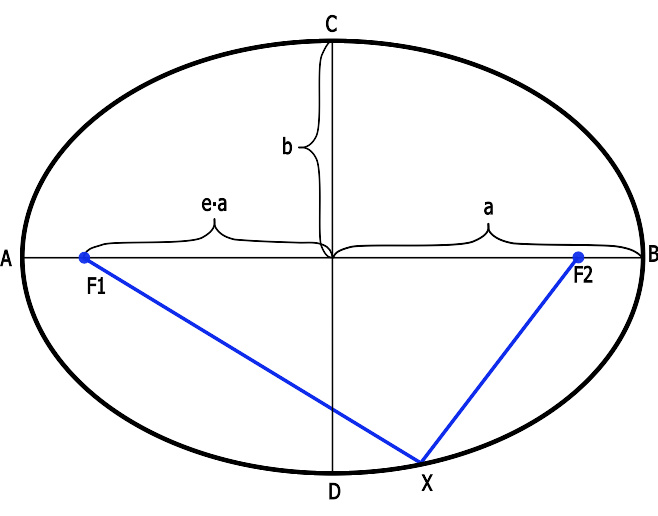
行星环绕太阳（焦点 F1 ）的椭圆轨道。

开普勒第一定律阐明，行星环绕太阳的轨道是椭圆形的。椭圆的面积是 π π -->ab{\displaystyle \pi ab} ；这里，a{\displaystyle a} 与 b{\displaystyle b} 分别为椭圆的半长轴与半短轴。在开普勒第二定律推导里，行星－太阳连线扫过区域速度 dAdt{\displaystyle {\frac {\mathrm {d} A}{\mathrm {d} t}}} 为

所以，行星公转周期 τ τ -->{\displaystyle \tau } 为

关于此行星环绕太阳，椭圆的半长轴 a{\displaystyle a} ，半短轴 b{\displaystyle b} 与近拱距rA{\displaystyle r_{A}} （近拱点A 与引力中心之间的距离），远拱距rB{\displaystyle r_{B}} （远拱点B 与引力中心之间的距离）的关系分别为

如果想要知道半长轴与半短轴，必须先求得近拱距与远拱距。依据能量守恒定律，

在近拱点 A 与远拱点 B，径向速度都等于零：

所以，

稍为加以编排，可以得到 r{\displaystyle r} 的一元二次方程：

其两个根分别为椭圆轨道的近拱距 rA{\displaystyle r_{A}} 与远拱距 rB{\displaystyle r_{B}} 。

代入方程 (6) 与 (7) ，

代入方程 (5) ，周期的方程为

Q.E.D.

参见

开普勒

牛顿第二定律

万有引力定律

《新天文学》

《世界的和谐》

牛顿旋转轨道定理

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。