定理

设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个单连通的开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\Omega \;\rightarrow \;\mathbb {C} }是一个Ω Ω -->{\displaystyle \Omega }上的全纯函数。设γ γ -->{\displaystyle \gamma }是Ω Ω -->{\displaystyle \Omega }内的一个分段可求长的简单闭曲线（即连续而不自交并且能定义长度的闭合曲线），那么：

单连通条件的必要性

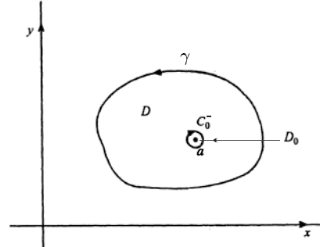
Ω Ω -->{\displaystyle \Omega }是单连通表示Ω Ω -->{\displaystyle \Omega }中没有“洞”，例如任何一个开圆盘D={z:|z− − -->z0|<r}{\displaystyle D=\{z:|z-z_{0}|都符合条件，这个条件是很重要的，考虑中央有“洞”的圆盘：Dh={z:0z0|<2}{\displaystyle D_单位圆=\{z:0 ，在其中取逆时针方向的单位圆路径：

考虑函数f:z↦ ↦ -->1/z{\displaystyle f\;:\;z\;\mapsto \;1/z}，它在Dh{\displaystyle D_{h}}中是全纯函数，但它的路径积分：

不等于零。这是因为函数f{\displaystyle f}在“洞”中有奇点。如果考虑整个圆盘Ds={z:|z− − -->z0|<2}{\displaystyle D_{s}=\{z:|z-z_{0}|<2\}}，就会发现f{\displaystyle f}在圆盘中央的点上没有定义，不是全纯函数。

等价叙述

柯西积分定理有若干个等价的叙述。例如： 设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\Omega \;\rightarrow \;\mathbb {C} }是一个定义在Ω Ω -->{\displaystyle \Omega }上的函数。设γ γ -->1:[0,1]→ → -->Ω Ω -->{\displaystyle \gamma _{1}\;:\;[0,1]\;\rightarrow \Omega }与γ γ -->2:[0,1]→ → -->Ω Ω -->{\displaystyle \gamma _{2}\;:\;[0,1]\;\rightarrow \Omega }是Ω Ω -->{\displaystyle \Omega }内的两条可求长的简单曲线，它们的起点和终点都重合：

并且函数f{\displaystyle f}在γ γ -->1{\displaystyle \gamma _{1}}与γ γ -->2{\displaystyle \gamma _{2}}围成的闭合区域D{\displaystyle D}内是全纯函数，那么函数f{\displaystyle f}沿这两条曲线的路径积分相同：

推广

除了对分段可求长的简单闭合曲线成立以外，柯西积分定理对于某些更复杂的曲线也适用。设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\Omega \;\rightarrow \;\mathbb {C} }是定义在Ω Ω -->{\displaystyle \Omega }上的全纯函数。无论Ω Ω -->{\displaystyle \Omega }内的曲线γ γ -->{\displaystyle \gamma }是自交还是卷绕数多于1（围着某一点转了不止一圈），只要γ γ -->{\displaystyle \gamma }能够通过连续形变收缩为Ω Ω -->{\displaystyle \Omega }内的一点，就有：

证明

以下的证明对函数有较为严格的要求，但对物理学中的应用来说已经足够。设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\Omega \;\rightarrow \;\mathbb {C} }是定义在Ω Ω -->{\displaystyle \Omega }上的全纯函数，γ γ -->{\displaystyle \gamma }是Ω Ω -->{\displaystyle \Omega }内的可求长的简单闭合曲线。假设f{\偏导数playstyle f}的一阶偏导数也在Ω Ω -->{\displaystyle \Omega }上连续，那么可以根据格林定理作出证明。具体如下：

为了便于表达，将函数f{\displaystyle f}写为实部函数和虚部函数：f(z)=f(x+yi)=u(x+yi)+iv(x+yi).{\displaystyle f(z)=f(x+yi)=u(x+yi)+i\,v(x+yi).} 由于dz=dx+idy{\displaystyle \displaystyle dz=dx+i\,dy}，积分

依据格林定理，右端的两个环路积分都可以变形为γ γ -->{\displaystyle \gamma }围成的区域Dγ γ -->{\displaystyle D_{\gamma }}上的面积分。

另一方面，由于f{\displaystyle f}是全纯函数，所以它的实部函数和虚部函数满足柯西－黎曼方程：

所以以上的两个积分中的被积函数都是0，

因而积分也是0：

推论

该定理的一个直接推论，是在单连通域内全纯函数的路径积分可以用类似于微积分基本定理的方法来计算：设Ω Ω -->{\displaystyle \Omega }是复平面C{\displaystyle \mathbb {C} }的一个开子集。f:Ω Ω -->→ → -->C{\displaystyle f\;:\;\Omega \;\rightarrow \;\mathbb {C} }是一个Ω Ω -->{\displaystyle \Omega }上的全纯函数。函数f{\displaystyle f}在Ω Ω -->{\displaystyle \Omega }内的路径积分，只与积分的起点和终点有关，与中间经历的路径无关。假设，起点为a，则可以定义一个函数F:Ω Ω -->→ → -->C{\displaystyle F\;:\;\Omega \;\rightarrow \;\mathbb {C} }

其中的γ γ -->ab{\displaystyle \gamma _{a}^{b}}可以是任何以a为起点，b为终点的分段可求长简单曲线。函数F{\displaystyle F}被称为f{\displaystyle f}的（复）原函数或反导数函数。

柯西积分定理与柯西积分公式是等价的。从柯西积分定理可以推导出柯西积分公式和留数定理。

参见

柯西－黎曼方程

柯西积分公式

留数

参考来源

参考文献

Kaplan, W. "Integrals of Analytic Functions. Cauchy Integral Theorem." §9.8 in Advanced Calculus, 4th ed. Reading, MA: Addison-Wesley, pp. 594-598, 1991.

Knopp, K. "Cauchy"s Integral Theorem." Ch. 4 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part I. New York: Dover, pp. 47-60, 1996.

Krantz, S. G. "The Cauchy Integral Theorem and Formula." §2.3 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 26-29, 1999.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 363-367, 1953.

Woods, F. S. "Integral of a Complex Function." §145 in Advanced Calculus: A Course Arranged with Special Reference to the Needs of Students of Applied Mathematics. Boston, MA: Ginn, pp. 351-352, 1926.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。