立体角的定义

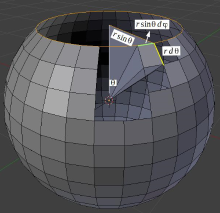
  立体角 d Ω Ω --> = sin ⁡ ⁡ --> θ θ --> d θ θ --> d φ φ --> {\displaystyle d\Omega =\sin \theta \,d\theta \,d\varphi }

以观测点为球心，构造一个单位球面；任意物体投影到该单位球面上的投影面积，即为该物体相对于该观测点的立体角。

因此，立体角是单位球面上的一块面积，这和“平面角是单位圆上的一段弧长”类似。

立体角公式

在球坐标系中，任意球面的极小面积为：

因此，极小立体角（单位球面上的极小面积）为：

所以，立体角是投影面积与球半径平方值的比，这和“平面角是圆的弧长与半径的比”类似。 对极小立体角做曲面积分即可得立体角：

任意定向曲面的立体角

任意定向曲面 S → → --> {\displaystyle {\vec {S}}} 相对于某一个点 P {\displaystyle P} 的立体角，即为该曲面投影到以 P {\displaystyle P} 为球心的单位球面上的面积。 令 r → → --> {\displaystyle {\vec {r}}} 为该单位球面上以 P {\displaystyle P} 为原点的极小面积的位置向量，可以得到以下公式：

立体角的单位

立体角的国际制单位是球面度（steradian，sr）。立体角有一个非国际制单位平方度，1 sr = (180/π)square degree。

封闭曲面的立体角

一个完整的球面对于球内任意一点的立体角为4π sr（对于球外任意一点的立体角为0 sr）：

这个定理对所有封闭曲面皆成立，它也是高斯定律的主要依据。

立体角的应用

立体角在物理上有相当多的应用：

计算电通量与磁通量，是高斯常用的数学方法。在高斯的环绕数中，也使用了立体角来推导出环绕数的公式。

计算发光强度。

常见几何体的立体角

圆锥，球冠

  球体中圆锥（1）与球冠（2）的切面。图中 θ = A/2，r = 1。

顶角为2 θ θ --> {\displaystyle \theta } 的圆锥的立体角为一个单位球的球冠。

（上面结果由下式得到）

应该注意阿基米德在2200年前不用微积分证明了球冠的表面积与半径为球冠边沿到球冠最低点的距离的圆的面积相等。球冠边沿到球冠最低点的距离为

显然，在单位圆中球冠立体角为

当 θ = π/2，球冠变为有着立体角 2π的半球。

当 θ = π，立体角涵盖整个球体，球冠变为有着立体角 4π的球，我们将4π称为全方位立体角。

任意四面体的立体角

对于任意一个四面体OABC,其中O,A,B,C分别为四面体的四个顶点。下面给出一个公式，计算从O点观察三角形ABC的立体角Ω的方便简单的公式。令α=∠BOC，β=∠AOC，γ=∠AOB(均为各自平面内两条直线的夹角，可以采用平面三角形的余弦公式计算求得)， s = 1 2 ( α α --> + β β --> + γ γ --> ) . {\displaystyle s={\frac {1}{2}}(\alpha +\beta +\gamma ).} 有(参见L" Huilier")

附上相应的Fortran 程序：

program solid_angleREAL X(4),Y(4),Z(4)!存放四个顶点的三维坐标，依次为A,B,C,O（程序中以P点代替，为观测点）X(1)=1X(2)=0X(3)=0X(4)=0Y(1)=0Y(2)=1Y(3)=0Y(4)=0Z(1)=0Z(2)=0Z(3)=1Z(4)=0!以单位1球体，在第一象限的八分之一球所含的四面体为例。程序可适用于任意四面体。!分别计算6条棱的长度的平方PA=(X(4)-X(1))**2+(Y(4)-Y(1))**2+(Z(4)-Z(1))**2PB=(X(4)-X(2))**2+(Y(4)-Y(2))**2+(Z(4)-Z(2))**2PC=(X(4)-X(3))**2+(Y(4)-Y(3))**2+(Z(4)-Z(3))**2AB=(X(1)-X(2))**2+(Y(1)-Y(2))**2+(Z(1)-Z(2))**2BC=(X(3)-X(2))**2+(Y(3)-Y(2))**2+(Z(3)-Z(2))**2AC=(X(1)-X(3))**2+(Y(1)-Y(3))**2+(Z(1)-Z(3))**2!应用余弦公式计算三个夹角COSALPHA=(PB+PC-BC)/2.0/SQRT(PB*PC)COSBETA=(PA+PC-AC)/2.0/SQRT(PA*PC)COSGAMA=(PB+PA-AB)/2.0/SQRT(PB*PA)ALPHA=acos((PB+PC-BC)/2.0/SQRT(PB*PC))BETA=acos((PA+PC-AC)/2.0/SQRT(PA*PC))GAMA=acos((PB+PA-AB)/2.0/SQRT(PB*PA))s=(alpha+beta+gama)/2.omiga=atan(sqrt(tan(s/2.)*tan(s/2.-alpha/2.)*tan(s/2.-beta/2.)*tan(s/2.-gama/2.)))*4.write(*,*)omiga*180./3.14159end

参考

^GB3102.1-1993：空间和时间的量和单位（代替GB 3102.1-1986）．1993年12月27日公布，1994年7月1日实施．

^Gauss"s Law - MIT

^GAUSS" LINKING NUMBER REVISITED

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。