分类

以角度分类

锐角三角形

锐角三角形的所有内角均为锐角（即小于90°）。

钝角三角形

钝角三角形是其中一角为钝角（大于90°）的三角形，其余两角均小于90°。

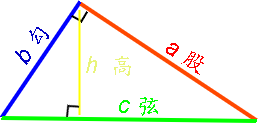
直角三角形

有一个角是直角（90°）的三角形为直角三角形。成直角的两条边称为“直角边”（cathetus），直角所对的边是“斜边”（hypotenuse）；或最长的边称为“弦”，底部的一边称作“勾”（又作“句”），另一边称为“股”。

直角三角形各边与角度的关系，可以三角比表示。详见三角函数。

以边长分类

不等边三角形

三条边边长皆不相等的三角形称为不等边三角形。

等边三角形

等边三角形（又称正三角形），为三边相等的三角形。其三个内角相等，均为60°。它是锐角三角形的一种。设其边长是 a {\displaystyle a} ，则其面积公式为 a 2 3 4 {\displaystyle {\frac {a^{2}{\sqrt {3}}}{4}}} 。

等边三角形是正四面体、正八面体和正二十面体这三个正多面体面的形状。六个边长相同的等边三角形可以拼成一个正六边形。

等腰三角形

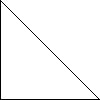
等腰直角三角形只有一种形状，其中两个角为45度。

等腰三角形是三条边中有两条边相等（或是其中两只内角相等）的三角形。等腰三角形中的两条相等的边被称为“腰”，而另一条边被称为“底边”，两条腰交叉组成的那个点被称为“顶点”，它们组成的角被称为“顶角”。

等边三角形和等腰直角三角形是等腰三角形的特殊形式。

退化三角形

退化三角形是指面积为零的三角形。满足下列条件之一的三角形即可称为退化三角形：三个内角的度数为(180°,0°,0°)或(90°,90°,0°)；三边其中一条边的长度为0；一条边的长度等于另外两条之和。有人认为退化三角形并不能算是三角形，这是由于它介乎于三角不等式之间，在一些资料中已否定了其中一条边等于其余两条边之和的情况。

一般性质

三角不等式

三角边长不等式

三角内外角不等式

角度

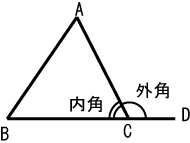
三角形外角

三角形内角和

毕氏定理

勾股定理

勾股定理逆定理

正弦定理

正弦定理：

余弦定理

余弦定理：

全等及相似

全等三角形

三角形具有稳定性，若二个三角形有以下的边角关系确定后，它的形状、大小就不会改变，二个三角形即为全等三角形。

SSS（Side-Side-Side，边、边、边）：各三角形的三条边的长度都对应地相等。

SAS（Side-Angle-Side，边、角、边）：各三角形的其中两条边的长度都对应地相等，且两条边夹着的角都对应地相等。

ASA（Angle-Side-Angle，角、边、角）：各三角形的其中两个角都对应地相等，且两个角夹着的边都对应地相等。

RHS（Right Angle-Hypotenuse-Side，直角、斜边、边）：在直角三角形中，斜边及另外一条直角边对应地相等。

AAS（Angle-Angle-Side，角、角、边）：各三角形的其中两个角都对应地相等，且其中一组对应角的对边也对应地相等。

注意，SSA（Side-Side-Angle、边、边、角）不能保证两个三角形全等，除非该角大于90°。

相似三角形

AA（Angle-Angle，角、角）：各三角形的其中两个角的都对应地相等。（或称AAA（Angle-Angle-Angle，角、角、角））

SSS（Side-Side-Side，边、边、边）：各三角形的三条边的长度都成同一比例。

SAS（Side-Angle-Side）：各三角形的两条边之长度都成同一比例，且两条边之夹角都对应地相等。

特殊线段

三角形中有着一些特殊线段，是三角形研究的重要对象。

中线(median)：三角形一边中点与这边所对顶点的连线段。

高线(altitude)：从三角形一个顶点向它的对边所作的垂线段。

角平分线(angle bisector)：平分三角形一角、一个端点在这一角的对边上的线段。

垂直平分线(perpendicular bisector)：通过三角形一边中点与该边所垂直的线段，又称中垂线。

以上特殊线段，每个三角形均有三条，且三线共点。

中线长度

设在 Δ Δ --> A B C {\displaystyle \Delta ABC\,} 中，若三边 a {\displaystyle a} 、 b {\displaystyle b} 、 c {\displaystyle c\,} 的中线分别为 m a {\displaystyle m_{a}} 、 m b {\displaystyle m_{b}} 、 m c {\displaystyle m_{c}} ，则：

高线长度

设在 Δ Δ --> A B C {\displaystyle \Delta ABC\,} 中，连接三个顶点 A {\displaystyle A} 、 B {\displaystyle B} 、 C {\displaystyle C} 上的高分别记作 h a {\displaystyle h_{a}} 、 h b {\displaystyle h_{b}} 、 h c {\displaystyle h_{c}} ，则：

其中 s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}} 。

角平分线长度

设在 Δ Δ --> A B C {\displaystyle \Delta ABC\,} 中，若三个角 A {\displaystyle A} 、 B {\displaystyle B} 、 C {\displaystyle C} 的角平分线分别为 t a {\displaystyle t_{a}} 、 t b {\displaystyle t_{b}} 、 t c {\displaystyle t_{c}} ，则：

三角形的心

三角形的内心、外心、垂心及形心称为三角形的四心，定义如下：

关于三角形的四心，有这样的一首诗：

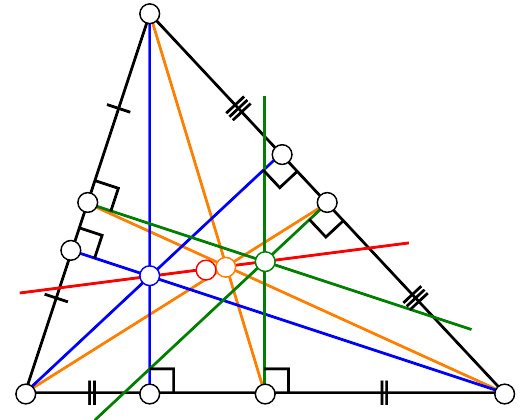
垂心（蓝）、形心（黄）和外心（绿）能连成一线，且成比例1:2，称为欧拉线。

连同以下的旁心，合称为三角形的五心：

外接圆和内切圆半径

设外接圆半径为 R {\displaystyle R} ， 内切圆半径为 r {\displaystyle r} ，则：

面积

基本公式

三角形的面积 A {\displaystyle A} 是底边 b {\displaystyle b} 与高 h {\displaystyle h} 乘积的一半，即：

其中的高是指底边与对角的垂直距离。

证明 三角形的面积可表示为一长方形面积的一半。 从右图可知，将两个全等三角形相拼，可得一平行四边形。而将该平行四边形分割填补，正好能得到一个面积等于 b h {\displaystyle bh} 的长方形。因此原来的三角形面积为 A = 1 2 b h {\displaystyle A={\frac {1}{2}}bh} 。 证毕。

已知两边及其夹角

设 a {\displaystyle a} 、 b {\displaystyle b} 为已知的两边， γ γ --> {\displaystyle \gamma } 为该两边的夹角，则三角形面积是：

证明 三角形的高 h 能以正弦的定义表示。 观察右图，根据正弦的定义： sin ⁡ ⁡ --> γ γ --> = h a {\displaystyle \sin \gamma ={\frac {h}{a}}} 。 因此： h = a sin ⁡ ⁡ --> γ γ --> {\displaystyle h=a\sin \gamma } 。 将此式代入基本公式，可得： A = 1 2 b ( a sin ⁡ ⁡ --> γ γ --> ) = 1 2 a b sin ⁡ ⁡ --> γ γ --> {\displaystyle A={\frac {1}{2}}b(a\sin \gamma )={\frac {1}{2}}ab\sin {\gamma }} 。 证毕。

已知两角及其夹边

β β --> {\displaystyle \beta } 、 γ γ --> {\displaystyle \gamma } 为已知的两角， a {\displaystyle a} 为该两角的夹边，则三角形面积是：

证明 三角形的面积能从两角及其夹边求得。 从正弦定理可知： b sin ⁡ ⁡ --> β β --> = a sin ⁡ ⁡ --> α α --> b = a sin ⁡ ⁡ --> β β --> sin ⁡ ⁡ --> α α --> {\displaystyle {\begin{aligned}{\frac {b}{\sin \beta }}&={\frac {a}{\sin \alpha }}\\b&={\frac {a\sin \beta }{\sin \alpha }}\\\end{aligned}}} 代入 A = 1 2 a b sin ⁡ ⁡ --> γ γ --> {\displaystyle A={\frac {1}{2}}ab\sin \gamma } ，得： A = a 2 sin ⁡ ⁡ --> β β --> sin ⁡ ⁡ --> γ γ --> 2 sin ⁡ ⁡ --> α α --> {\displaystyle A={\frac {a^{2}\sin \beta \sin \gamma }{2\sin \alpha }}} 。 注意到 α α --> + β β --> + γ γ --> = 180 ∘ ∘ --> {\displaystyle \alpha +\beta +\gamma =180^{\circ }} ，因此： A = a 2 sin ⁡ ⁡ --> β β --> sin ⁡ ⁡ --> γ γ --> 2 sin ⁡ ⁡ --> [ 180 ∘ ∘ --> − − --> ( β β --> + γ γ --> ) ] = a 2 sin ⁡ ⁡ --> β β --> sin ⁡ ⁡ --> γ γ --> 2 sin ⁡ ⁡ --> ( β β --> + γ γ --> ) {\displaystyle {\begin{aligned}A&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin[180^{\circ }-(\beta +\gamma )]}}\\&={\frac {a^{2}\sin \beta \sin \gamma }{2\sin(\beta +\gamma )}}\\\end{aligned}}} 证毕。

已知三边长

希罗公式，又称海伦公式，其表示形式为：

其中 s {\displaystyle s} 等于三角形的半周长，即：

秦九韶亦求过类似的公式，称为 三斜求积法 ：

也有用幂和来表示的公式：

亦可用Cayley–Menger行列式表示的公式：

基于希罗公式在三角形拥有非常小的角度时并不数值稳定，有一个变化的计法。设 a ≥ ≥ --> b ≥ ≥ --> c {\displaystyle a\geq b\geq c} ，三角形面积为：

证明 设 a {\displaystyle a} 、 b {\displaystyle b} 、 c {\displaystyle c} 为三角形三条边， α α --> {\displaystyle \alpha } 、 β β --> {\displaystyle \beta } 、 γ γ --> {\displaystyle \gamma } 为相应边的对角。从余弦定理可知： cos ⁡ ⁡ --> γ γ --> = a 2 + b 2 − − --> c 2 2 a b {\displaystyle \cos \gamma ={\frac {a^{2}+b^{2}-三角恒等式}{2ab}}} 以毕氏三角恒等式可得： sin ⁡ ⁡ --> γ γ --> = 1 − − --> cos 2 ⁡ ⁡ --> γ γ --> = 4 a 2 b 2 − − --> ( a 2 + b 2 − − --> c 2 ) 2 2 a b {\displaystyle \sin \gamma ={\sqrt {1-\cos ^{2}\gamma }}={\frac {\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}{2ab}}} 。 将此式代入 A = 1 2 a b sin ⁡ ⁡ --> γ γ --> {\displaystyle A={\frac {1}{2}}ab\sin {\gamma }} ，得： A = 1 4 4 a 2 b 2 − − --> ( a 2 + b 2 − − --> c 2 ) 2 {\displaystyle A={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}} 。 因式分解及简化后可得： A = 1 4 ( a + b + c ) ( a + b − − --> c ) ( a + c − − --> b ) ( b + c − − --> a ) {\displaystyle A={\frac {1}{4}}{\sqrt {\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)}}} 代入 s = a + b + c 2 {\displaystyle s={\frac {a+b+c}{2}}} ，即可证毕。

已知坐标系中三顶点坐标

由 ( x 1 , y 1 ) {\displaystyle (x_{1},y_{1})} 、 ( x 2 , y 2 ) {\displaystyle (x_{2},y_{2})} 及 ( x 3 , y 3 ) {\displaystyle (x_{3},y_{3})} 三个顶点构成的三角形，其面积可用行列式的绝对值表示：

证明 无论三角形的顶点位置如何，该三角形总可以用一个直角梯形（或矩形）和两个直角三角形面积的和差来表示，而在直角坐标系中，已知直角梯形（或矩形）和直角三角形的顶点的坐标，该三角形的面积容易求出，即用上述的行列式表示。

若三个顶点设在三维座标系上，即由 ( x 1 , y 1 , z 1 ) {\displaystyle (x_{1},y_{1},z_{1})} 、 ( x 2 , y 2 , z 2 ) {\displaystyle (x_{2},y_{2},z_{2})} 及 ( x 3 , y 3 , z 3 ) {\displaystyle (x_{3},y_{3},z_{3})} 三个顶点构成三角形，其面积等于各自在主平面上投影面积的毕氏和，即：

已知周界及内切圆或外接圆半径

设三角形三边边长分别为 a {\displaystyle a} 、 b {\displaystyle b} 及 c {\displaystyle c} ，三角形半周长（ a + b + c 2 {\displaystyle {\frac {a+b+c}{2}}} ）为 s {\displaystyle s} ，内切圆半径为 r {\displaystyle r} ，则：

若设外接圆半径为 R {\displaystyle R} ，则：

证明 内切圆半径公式 三角形被三条角平分线分成三分。 根据右图，设 A B = c {\displaystyle AB=c} ， b = A C {\displaystyle b=AC} ， B C = a {\displaystyle BC=a} ，则三角形面积可表示为： A = 1 2 a r + 1 2 b r + 1 2 c r = r ( a + b + c ) 2 = r s {\displaystyle {\begin{aligned}A&={\frac {1}{2}}ar+{\frac {1}{2}}br+{\frac {1}{2}}cr\\&={\frac {r(a+b+c)}{2}}\\&=rs\end{aligned}}} 外接圆半径公式 根据正弦定理： c sin ⁡ ⁡ --> γ γ --> = 2 R sin ⁡ ⁡ --> γ γ --> = c 2 R {\displaystyle {\begin{aligned}{\frac {c}{\sin \gamma }}&=2R\\\sin \gamma &={\frac {c}{2R}}\\\end{aligned}}} 因此： A = 1 2 a b sin ⁡ ⁡ --> γ γ --> = 1 2 a b ( c 2 R ) = a b c 4 R {\displaystyle {\begin{aligned}A&={\frac {1}{2}}ab\sin \gamma \\&={\frac {1}{2}}ab\left({\frac {c}{2R}}\right)\\&={\frac {abc}{4R}}\end{aligned}}}

已知两边向量

设从一角出发，引出两边的向量为 a {\displaystyle \mathbf {a} } 及 b {\displaystyle \mathbf {b} } ，三角形的面积为：

证明 根据向量积定义， | a × × --> b | = | a | | b | sin ⁡ ⁡ --> γ γ --> {\displaystyle |\mathbf {a} \times \mathbf {b} |=|\mathbf {a} ||\mathbf {b} |\sin \gamma } ， 其中 γ γ --> {\displaystyle \gamma } 是两支向量的夹角。 因此： 1 2 | a × × --> b | = 1 2 | a | | b | sin ⁡ ⁡ --> γ γ --> = A {\displaystyle {\frac {1}{2}}|\mathbf {a} \times \mathbf {b} |={\frac {1}{2}}|\mathbf {a} ||\mathbf {b} |\sin \gamma =A} 证毕。

半角定理

在三角形 A B C {\displaystyle ABC\,} 中，三个角的半角的正切和三边有如下关系：

证明 以正弦及余弦之比表示正切： tan ⁡ ⁡ --> A 2 = sin ⁡ ⁡ --> A 2 cos ⁡ ⁡ --> A 2 {\displaystyle \tan {\frac {A}{2}}={\frac {\sin {\frac {A}{2}}}{\cos {\frac {A}{2}}}}} 因为 sin ⁡ ⁡ --> A 2 > 0 {\displaystyle \sin {\frac {A}{2}}>0} tan ⁡ ⁡ --> A 2 > 0 {\displaystyle \tan {\frac {A}{2}}>0} 所以 sin ⁡ ⁡ --> A 2 = 1 − − --> cos ⁡ ⁡ --> A 2 = 1 2 ( 1 − − --> b 2 + c 2 − − --> a 2 2 b c ) {\displaystyle \sin {\frac {A}{2}}={\sqrt {\frac {1-\cos {A}}{2}}}={\sqrt {{\frac {1}{2}}\left(1-{\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)}}} = a 2 − − --> ( b − − --> c ) 2 4 b c {\displaystyle ={\sqrt {\frac {a^{2}-{\left(b-c\right)}^{2}}{4bc}}}} = ( a + b − − --> c ) ( a + c − − --> b ) 4 b c {\displaystyle ={\sqrt {\frac {\left(a+b-c\right)\left(a+c-b\right)}{4bc}}}} 而 cos ⁡ ⁡ --> A 2 = 1 + cos ⁡ ⁡ --> A 2 = 1 2 ( 1 + b 2 + c 2 − − --> a 2 2 b c ) {\displaystyle \cos {\frac {A}{2}}={\sqrt {\frac {1+\cos {A}}{2}}}={\sqrt {{\frac {1}{2}}\left(1+{\frac {b^{2}+c^{2}-a^{2}}{2bc}}\right)}}} = ( b + c ) 2 − − --> a 2 4 b c {\displaystyle ={\sqrt {\frac {{\left(b+c\right)}^{2}-a^{2}}{4bc}}}} = ( b + c + a ) ( b + c − − --> a ) 4 b c {\displaystyle ={\sqrt {\frac {\left(b+c+a\right)\left(b+c-a\right)}{4bc}}}} 所以 tan ⁡ ⁡ --> A 2 = sin ⁡ ⁡ --> A 2 cos ⁡ ⁡ --> A 2 = ( a + b − − --> c ) ( a + c − − --> b ) 4 b c ( b + c + a ) ( b + c − − --> a ) 4 b c = ( a + b − − --> c ) ( a + c − − --> b ) ( b + c + a ) ( b + c − − --> a ) {\displaystyle {\begin{aligned}\tan {\frac {A}{2}}&={\frac {\sin {\frac {A}{2}}}{\cos {\frac {A}{2}}}}\\&={\frac {\sqrt {\cfrac {(a+b-c)(a+c-b)}{4bc}}}{\sqrt {\cfrac {(b+c+a)(b+c-a)}{4bc}}}}\\&={\sqrt {\frac {(a+b-c)(a+c-b)}{(b+c+a)(b+c-a)}}}\end{aligned}}} 即 tan ⁡ ⁡ --> A 2 = 1 b + c − − --> a ( b + c − − --> a ) ( a + c − − --> b ) ( a + b − − --> c ) a + b + c {\displaystyle \tan {\frac {A}{2}}={\frac {1}{b+c-a}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}} 同理可得 tan ⁡ ⁡ --> B 2 = 1 a + c − − --> b ( b + c − − --> a ) ( a + c − − --> b ) ( a + b − − --> c ) a + b + c {\displaystyle \tan {\frac {B}{2}}={\frac {1}{a+c-b}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}} tan ⁡ ⁡ --> C 2 = 1 a + b − − --> c ( b + c − − --> a ) ( a + c − − --> b ) ( a + b − − --> c ) a + b + c {\displaystyle \tan {\frac {C}{2}}={\frac {1}{a+b-c}}{\sqrt {\frac {\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)}{a+b+c}}}}

其他三角形有关的定理

外角定理

拿破仑三角形

费马点

欧拉线

梅涅劳斯定理

参看

三角学

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。