基本定义

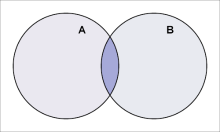
A和B的交集

A 和 B 的交集写作" A ∩ B "。形式上：

例如：集合{1, 2, 3}和{2, 3, 4}的交集为{2, 3}。数字9 不 属于素数集合{2, 3, 5, 7, 11,…}和奇数集合{1, 3, 5, 7, 9, 11,…}的交集。

若两个集合 A 和 B 的交集为空，就是说他们没有公共元素，则他们 不相交 ，写作： A ∩ B = Ø。例如集合{1, 2}和{3, 4}不相交，写作{1, 2} ∩{3, 4} = Ø。

更一般的，交集运算可以对多个集合同时进行。例如，集合 A ， B ， C 和 D 的 交集 为 A ∩ B ∩ C ∩ D = A ∩( B ∩( C ∩ D ))。交集运算满足结合律，即 A ∩( B ∩ C ) =( A ∩ B )∩ C 。

任意交集

以上定义可推广到任意 非空 集合的集合的交集。若 M 是一个非空集合，其元素本身也是集合，则 x 属于 M 的 交集 ，当且仅当对任意 M 的元素 A ， x 属于 A 。符号表示为：

这一概念也蕴涵了前述的定义，例如， A ∩ B ∩ C 是集合{ A , B , C }的交集。 （若 M 为空集，有时候谈论它的交集也是有意义的，请见空交集）。

这一概念的表示符号有多种。集合论者有时用" ∩ M "，有时用" ∩ A ∈ M A "。后一种写法可以一般化为" ∩ i ∈ I A i "，表示集合{ A i : i ∈ I }的交集。这里 I 非空，而对于每个 I 里的 i ， A i 是一个集合。

当索引集 I 为自然数集合时，这种符号表示与无限序列相类似：

为了排版方便，上述符号也可以写成" A 1 ∩ A 2 ∩ A 3 ∩ ..."，尽管严格说来，像 A 1 ∩ （ A 2 ∩ ( A 3 ∩ ...这样的写法是无意义的。（这个例子是可数个集合的交集，非常常用；可以参看σ-代数条目中的例子。）

最后，注意当符号"∩"写在其他符号 之前 ，而不是 之间 的时候，需要写得大一号。（在HTML中，可以使用字体 ⋂ ，或者尝试 ∩ 。）

参见

朴素集合论

并集

补集

对称差

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。