



卷积
简单介绍
卷积是分析数学中一种重要的运算。设:f(x){\displaystyle f(x)},g(x){\displaystyle g(x)}是R{\displaystyle \mathbb {R} }上的两个可积函数,作积分:
可以证明,关于几乎所有的x∈ ∈ -->(− − -->∞ ∞ -->,∞ ∞ -->){\displaystyle x\in (-\infty ,\infty )},上述积分是存在的。这样,随着x{\displaystyle x}的不同取值,这个积分就定义了一个新函数h(x){\displaystyle h(x)},称为函数f{\displaystyle f}与g{\displaystyle g}的卷积,记为h(x)=(f∗ ∗ -->g)(x){\displaystyle h(x)=(f*g)(x)}。我们可以轻易验证:(f∗ ∗ -->g)(x)=(g∗ ∗ -->f)(x){\displaystyle (f*g)(x)=(g*f)(x)},并且(f∗ ∗ -->g)(x){\displaystyle (f*g)(x)}仍为可积函数。这就是说,把卷积代替乘法,L1(R1){\displaystyle 巴拿赫1}(R^{1})}空间是一个代数,甚至是巴拿赫代数。虽然这里为了方便我们假设 f,g∈ ∈ -->L1(R){\displaystyle \textstyle f,g\in L^{1}(\mathbb {R} )},不过卷积只是运算符号,理论上并不需要对函数 f,g{\displaystyle f,g} 有特别的限制,虽然常常要求 f,g{\displaystyle f,g} 至少是可测函数(measurable function)(如果不是可测函数的话,积分可能根本没有意义),至于生成的卷积函数性质会在运算之后讨论。
卷积与傅里叶变换有着密切的关系。例如两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,利用此一性质,能简化傅里叶分析中的许多问题。
由卷积得到的函数f∗ ∗ -->g{\displaystyle f*g}一般要比f{\displaystyle f}和g{\displaystyle g}都光滑。特别当g{\displaystyle g}为具有紧支集的光滑函数,f{\displaystyle f}为局部可积时,它们的卷积f∗ ∗ -->g{\displaystyle f*g}也是光滑函数。利用这一性质,对于任意的可积函数f{\displaystyle f},都可以简单地构造出一列逼近于f{\displaystyle f}的光滑函数列fs{\displaystyle f_{s}},这种方法称为函数的光滑化或正则化。
卷积的概念还可以推广到数列、测度以及广义函数上去。
定义
函数f,g{\displaystyle f,g} 是定义在 Rn{\displaystyle \mathbb {R} ^{n}} 上的可测函数(measurable function),f与g的卷积记作f∗ ∗ -->g{\displaystyle f*g},它是其中一个函数翻转并平移后与另一个函数的乘积的积分,是一个对平移量的函数。,也就是:
如果函数不是定义在 Rn{\displaystyle \mathbb {R} ^{n}} 上,可以把函数定义域以外的值都规定成零,这样就变成一个定义在 Rn{\displaystyle \mathbb {R} ^{n}} 上的函数。
离散卷积
对于定义在整数 Z{\displaystyle \mathbb {Z} } 上的函数 f,g{\displaystyle f,g},卷积定义为
这里一样把函数定义域以外的值当成零,所以可以扩展函数到所有整数上(如果本来不是的话)。
当g[n]{\displaystyle g[n]} 的支撑集(support)为有限长度M{\displaystyle M},上式会变成有限和:
计算离散卷积的方法
计算卷积f[n]∗ ∗ -->g[n]{\displaystyle f[n]*g[n]}有三种主要的方法,分别为
直接计算(Direct Method)
快速傅里叶变换(FFT)
分段卷积(sectioned convolution)
方法1是直接利用定义来计算卷积,而方法2和3都是用到了FFT来快速计算卷积。也有不需要用到FFT的作法,如使用数论变换。
方法1:直接计算
作法:利用卷积的定义
若f[n]{\displaystyle f[n]}和g[n]{\displaystyle g[n]}皆为实数信号,则需要MN{\displaystyle MN}个乘法。
若f[n]{\displaystyle f[n]}和g[n]{\displaystyle g[n]}皆为更一般性的复数信号,不使用复数乘法的快速算法,会需要4MN{\displaystyle 4MN}个乘法;但若使用复数乘法的快速算法,则可简化至3MN{\displaystyle 3MN}个乘法。
方法2:快速傅里叶变换(FFT)
概念:由于两个离散信号在时域(time domain)做卷积相当于这两个信号的离散傅里叶变换在频域(frequency domain)做相乘:
作法:因此这个方法即是先将信号从时域转成频域:
特别注意DFT和IDFT的点数P{\displaystyle P}要满足P≥ ≥ -->M+N− − -->1{\displaystyle P\geq M+N-1}。
由于DFT有快速算法FFT,所以运算量为O(Plog2 -->P){\displaystyle O(P\log _{2}P)}
假设P{\displaystyle P}点DFT的乘法量为a{\displaystyle a},f[n]{\displaystyle f[n]}和g[n]{\displaystyle g[n]}为一般性的复数信号,并使用复数乘法的快速算法,则共需要3a+3P{\displaystyle 3a+3P}个乘法。
方法3:分段卷积(sectioned convolution)
概念:将f[n]{\displaystyle f[n]}切成好几段,每一段分别和g[n]{\displaystyle g[n]}做卷积后,再将结果相加。
作法:先将f[n]{\displaystyle f[n]}切成每段长度为L{\displaystyle L}的区段(L>M{\displaystyle L>M}),假设共切成S段:
总共只需要做P{\displaystyle P}点FFT 2S+1{\displaystyle 2S+1}次,因为g[n]{\displaystyle g[n]}只需要做一次FFT。
假设P{\displaystyle P}点DFT的乘法量为a{\displaystyle a},f[n]{\displaystyle f[n]}和g[n]{\displaystyle g[n]}为一般性的复数信号,并使用复数乘法的快速算法,则共需要(2S+1)a+3SP{\displaystyle (2S+1)a+3SP}个乘法。
运算量:NL3(L+M− − -->1)[log2 -->(L+M− − -->1)+1]{\displaystyle {\frac {N}{L}}3(L+M-1)[\log _{2}(L+M-1)+1]}
运算复杂度:O(N){\displaystyle O(N)},和N{\displaystyle N}呈线性,较方法2小。
分为 Overlap-Add 和 Overlap-Save 两种方法。
分段卷积: Overlap-Add
欲做x[n]∗ ∗ -->h[n]{\displaystyle x[n]*h[n]}的分段卷积分,x[n]{\displaystyle x[n]} 长度为 N{\displaystyle N},h[n]{\displaystyle h[n]} 长度为 M{\displaystyle M},
Step 1: 将x[n]{\displaystyle x[n]}每 L{\displaystyle L} 分成一段
Step 2: 再每段 L{\displaystyle L} 点后面添加 M− − -->1{\displaystyle M-1} 个零,变成长度 L+M− − -->1{\displaystyle L+M-1}
Step 3: 把 h[n]{\displaystyle h[n]} 添加 L− − -->1{\displaystyle L-1}个零,变成长度 L+M− − -->1{\displaystyle L+M-1}的 h′[n]{\displaystyle h"[n]}
Step 4: 把每个 x[n]{\displaystyle x[n]} 的小段和 h′[n]{\displaystyle h"[n]} 做快速卷积,也就是IDFTL+M− − -->1{DFTL+M− − -->1(x[n])DFTL+M− − -->1(h′[n])}{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h"[n])}\}},每小段会得到长度 L+M− − -->1{\displaystyle L+M-1} 的时域信号
Step 5: 放置第 i{\displaystyle i} 个小段的起点在位置 L× × -->i{\displaystyle L\times i} 上, i=0,1,...,⌈ ⌈ -->NL⌉ ⌉ -->− − -->1{\displaystyle i=0,1,...,\lceil {\frac {N}{L}}\rceil -1}
Step 6: 会发现在每一段的后面 M− − -->1{\displaystyle M-1} 点有重叠,将所有点都相加起来,顾名思义 Overlap-Add,最后得到结果
举例来说:
x[n]=[1,2,3,4,5,− − -->1,− − -->2,− − -->3,− − -->4,− − -->5,1,2,3,4,5]{\displaystyle x[n]=[1,2,3,4,5,-1,-2,-3,-4,-5,1,2,3,4,5]}, 长度 N=15{\displaystyle N=15}
h[n]=[1,2,3]{\displaystyle h[n]=[1,2,3]}, 长度 M=3{\displaystyle M=3}
令 L=5{\displaystyle L=5}
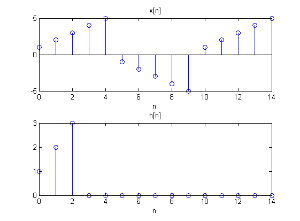
x[n]和h[n]
令 L=5{\displaystyle L=5} 切成三段,分别为 x0[n],x1[n],x2[n]{\displaystyle x_{0}[n],x_{1}[n],x_{2}[n]}, 每段填 M− − -->1{\displaystyle M-1} 个零,并将 h[n]{\displaystyle h[n]} 填零至长度 L+M− − -->1{\displaystyle L+M-1}
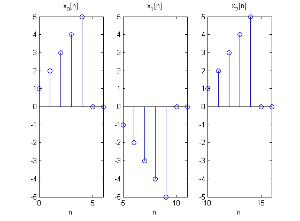
分段x[n]
将每一段做IDFTL+M− − -->1{DFTL+M− − -->1(x[n])DFTL+M− − -->1(h′[n])}{\displaystyle IDFT_{L+M-1}\{{DFT_{L+M-1}(x[n])DFT_{L+M-1}(h"[n])}\}}
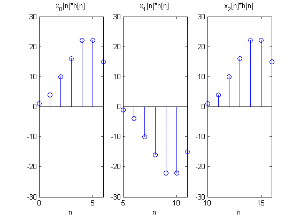
分段运算结果
若将每小段摆在一起,可以注意到第一段的范围是 0∼ ∼ -->6{\displaystyle 0\thicksim 6} ,第二段的范围是 5∼ ∼ -->11{\displaystyle 5\thicksim 11},第三段的范围是 10∼ ∼ -->16{\displaystyle 10\thicksim 16},三段的范围是有重叠的
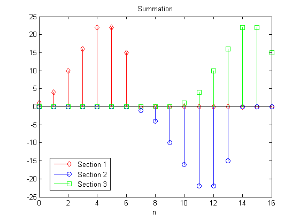
合并分段运算结果
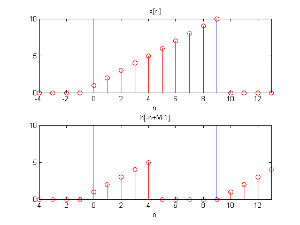
最后将三小段加在一起,并将结果和未分段的卷积做比较,上图是分段的结果,下图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
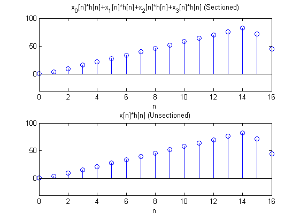
结果比较图
分段卷积: Overlap-Save
欲做x[n]∗ ∗ -->h[n]{\displaystyle x[n]*h[n]}的分段卷积分,x[n]{\displaystyle x[n]} 长度为 N{\displaystyle N},h[n]{\displaystyle h[n]} 长度为 M{\displaystyle M},
Step 1: 将 x[n]{\displaystyle x[n]} 前面填 M− − -->1{\displaystyle M-1} 个零
Step 2: 第一段 i=0{\displaystyle i=0}, 从新的 x[n]{\displaystyle x[n]} 中 L× × -->i− − -->(M− − -->1)× × -->i{\displaystyle L\times i-(M-1)\times i} 取到 L× × -->(i+1)− − -->(M− − -->1)× × -->i− − -->1{\displaystyle L\times (i+1)-(M-1)\times i-1} 总共 L{\displaystyle L} 点当做一段,因此每小段会重复取到前一小段的 M− − -->1{\displaystyle M-1} 点,取到新的一段全为零为止
Step 3: 把 h[n]{\displaystyle h[n]} 添加 L− − -->M{\displaystyle L-M} 个零,变成长度 L{\displaystyle L} 的 h′[n]{\displaystyle h"[n]}
Step 4: 把每个 x[n]{\displaystyle x[n]} 的小段和 h′[n]{\displaystyle h"[n]} 做快速卷积,也就是IDFTL{DFTL(x[n])DFTL(h′[n])}{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h"[n])}\}},每小段会得到长度 L{\displaystyle L} 的时域信号
Step 5: 对于每个 i{\displaystyle i} 小段,只会保留末端的 L− − -->(M− − -->1){\displaystyle L-(M-1)} 点,因此得名 Overlap-Save
Step 6: 将所有保留的点合再一起,得到最后结果
举例来说:
x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]}, 长度 N=15{\displaystyle N=15}
h[n]=[1,2,3]{\displaystyle h[n]=[1,2,3]}, 长度 M=3{\displaystyle M=3}
令 L=7{\displaystyle L=7}
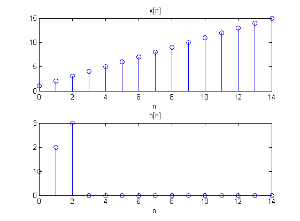
x[n]和h[n]
将 x[n]{\displaystyle x[n]} 前面填 M− − -->1{\displaystyle M-1} 个零以后,按照 Step 2 的方式分段,可以看到每一段都重复上一段的 M− − -->1{\displaystyle M-1} 点
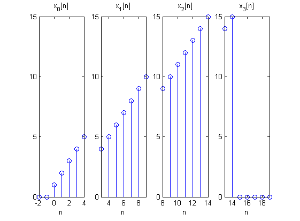
分段x[n]
再将每一段做 IDFTL{DFTL(x[n])DFTL(h′[n])}{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h"[n])}\}}以后可以得到
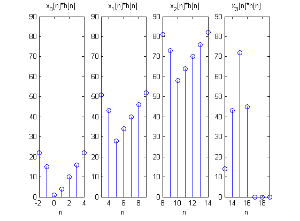
分段运算结果
保留每一段末端的 L− − -->(M− − -->1){\displaystyle L-(M-1)} 点,摆在一起以后,可以注意到第一段的范围是 0∼ ∼ -->4{\displaystyle 0\thicksim 4} ,第二段的范围是 5∼ ∼ -->9{\displaystyle 5\thicksim 9},第三段的范围是 10∼ ∼ -->14{\displaystyle 10\thicksim 14},第四段的范围是 15∼ ∼ -->16{\displaystyle 15\thicksim 16},四段的范围是没有重叠的
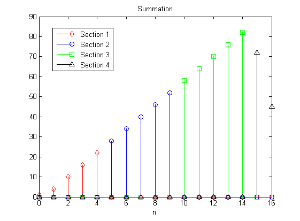
合并分段运算结果
将结果和未分段的卷积做比较,下图是分段的结果,上图是没有分段并利用快速卷积所算出的结果,验证两者运算结果相同。
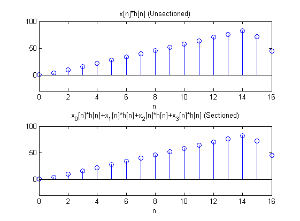
结果比较图
至于为什么要把前面 M− − -->1{\displaystyle M-1} 丢掉?
以下以一例子来阐述:
x[n]=[1,2,3,4,5,6,7,8,9,10]{\displaystyle x[n]=[1,2,3,4,5,6,7,8,9,10]}, 长度 L=10{\displaystyle L=10},
h[n]=[1,2,3,4,5]{\displaystyle h[n]=[1,2,3,4,5]}, 长度 M=5{\displaystyle M=5},
第一条蓝线代表 y{\displaystyle y} 轴,而两条蓝线之间代表长度 L{\displaystyle L},是在做快速卷积时的周期
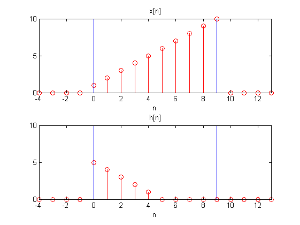
x[n]和h[n]
当在做快速卷积时IDFTL{DFTL(x[n])DFTL(h′[n])}{\displaystyle IDFT_{L}\{{DFT_{L}(x[n])DFT_{L}(h"[n])}\}},是把信号视为周期 L{\displaystyle L},在时域上为循环卷积分,
而在一开始前 M− − -->1{\displaystyle M-1} 点所得到的值,是 h[0],h[6],h[7],h[8],h[9]{\displaystyle h[0],h[6],h[7],h[8],h[9]} 和 x[0],x[6],x[7],x[8],x[9]{\displaystyle x[0],x[6],x[7],x[8],x[9]} 内积的值,
然而 h[6],h[7],h[8],h[9]{\displaystyle h[6],h[7],h[8],h[9]} 这 M− − -->1{\displaystyle M-1} 个值应该要为零,以往在做快速卷积时长度为 L+M− − -->1{\displaystyle L+M-1} 时不会遇到这些问题,
而今天因为在做快速卷积时长度为 L{\displaystyle L} 才会把这 M− − -->1{\displaystyle M-1} 点算进来,因此我们要丢弃这 M− − -->1{\displaystyle M-1} 点内积的结果
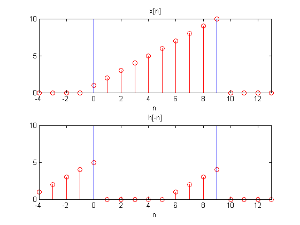
循环卷积
为了要丢弃这 M− − -->1{\displaystyle M-1} 点内积的结果,位移 h[− − -->n]{\displaystyle h[-n]}M− − -->1{\displaystyle M-1} 点,并把位移以后内积合的值才算有效。
位移以后内积
应用时机
以上三种方法皆可用来计算卷积,其差别在于所需总体乘法量不同。基于运算量以及效率的考量,在计算卷积时,通常会选择所需总体乘法量较少的方法。
以下根据f[n]{\displaystyle f[n]}和g[n]{\displaystyle g[n]}的长度(N,M{\displaystyle N,M})分成5类,并列出适合使用的方法:
M{\displaystyle M}为一非常小的整数 - 直接计算
M≪ ≪ -->N{\displaystyle M\ll N} - 分段卷积
M≈ ≈ -->N{\displaystyle M\approx N} - 快速傅里叶变换
M≫ ≫ -->N{\displaystyle M\gg N} - 分段卷积
N{\displaystyle N}为一非常小的整数 - 直接计算
基本上,以上只是粗略的分类。在实际应用时,最好还是算出三种方法所需的总乘法量,再选择其中最有效率的方法来计算卷积。
例子
Q1:当N=2000,M=17{\displaystyle N=2000,M=17},适合用哪种方法计算卷积?
Ans:
因此,当N=2000,M=17{\displaystyle N=2000,M=17},所需总乘法量:分段卷积
Q2:当N=1024,M=3{\displaystyle N=1024,M=3},适合用哪种方法计算卷积?
Ans:
因此,当N=1024,M=3{\displaystyle N=1024,M=3},所需总乘法量:分段卷积
虽然当M{\displaystyle M}是个很小的正整数时,大致上适合使用直接计算。但实际上还是将3个方法所需的乘法量都算出来,才能知道用哪种方法可以达到最高的效率。
Q3:当N=1024,M=600{\displaystyle N=1024,M=600},适合用哪种方法计算卷积?
Ans:
因此,当N=1024,M=600{\displaystyle N=1024,M=600},所需总乘法量:快速傅里叶变换 = 分段卷积
多元函数卷积
按照翻转、平移、积分的定义,还可以类似的定义多元函数上的积分:
性质
各种卷积算子都满足下列性质:
其中a{\displaystyle a}为任意实数(或复数)。
其中Df表示f的微分,如果在离散域中则是指差分算子,包括前向差分与后向差分两种:
前向差分:D+f(n)=f(n+1)− − -->f(n){\displaystyle {\mathcal {D}}^{+}f(n)=f(n+1)-f(n)}
后向差分:D− − -->f(n)=f(n)− − -->f(n− − -->1){\displaystyle {\mathcal {D}}^{-}f(n)=f(n)-f(n-1)}
卷积定理
卷积定理指出,函数卷积的傅里叶变换是函数傅里叶变换的乘积。即,一个域中的卷积相当于另一个域中的乘积,例如时域中的卷积就对应于频域中的乘积。
其中F(f){\displaystyle {\mathcal {F}}(f)}表示f的傅里叶变换。
这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换(参见Mellin inversion theorem(英语:Mellin inversion theorem))等各种傅里叶变换的变体同样成立。在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。
利用卷积定理可以简化卷积的运算量。对于长度为n{\displaystyle n}的序列,按照卷积的定义进行计算,需要做2n− − -->1{\displaystyle 2n-1}组对位乘法,其计算复杂度为O(n2){\displaystyle {\mathcal {O}}(n^{2})};而利用傅里叶变换将序列变换到频域上后,只需要一组对位乘法,利用傅里叶变换的快速算法之后,总的计算复杂度为O(nlog -->n){\displaystyle {\mathcal {O}}(n\log n)}。这一结果可以在快速乘法计算中得到应用。
在群上的卷积
若G是有某m测度的群(例如豪斯多夫空间上哈尔测度下局部紧致的拓扑群),对于G上m-勒贝格可积的实数或复数函数f和g,可定义它们的卷积:
对于这些群上定义的卷积同样可以给出诸如卷积定理等性质,但是这需要对这些群的表示理论以及调和分析的彼得-外尔定理。
应用
卷积在科学、工程和数学上都有很多应用:
图像处理中,用作图像模糊、锐化、边缘检测。
统计学中,加权的滑动平均是一种卷积。
概率论中,两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
声学中,回声可以用源声与一个反映各种反射效应的函数的卷积表示。
电子工程与信号处理中,任一个线性系统的输出都可以通过将输入信号与系统函数(系统的冲激响应)做卷积获得。
物理学中,任何一个线性系统(符合叠加原理)都存在卷积。
参见
反卷积
傅里叶变换
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。

- 有价值
- 一般般
- 没价值








24小时热门
推荐阅读
关于我们

APP下载


















