基本描述

自动机是有限状态机（FSM）的数学模型。FSM是给定符号输入，依据（可表达为一个表格的）转移函数“跳转”过一系列状态的一种机器。在常见的FSM的“米利型有限状态机”（Mealy）变体中，这个转移函数告诉自动机给定当前状态和当前字符的时候下一个状态是什么。

逐个读取输入中的符号，直到被完全耗尽(把它当作有一个字写在其上的磁带，通过自动机的读磁头来读取它；磁头在磁带上前行移动，一次读一个符号)。一旦输入被耗尽，自动机被称为“停止”了。

依赖自动机停止时的状态，称呼这个自动机要么是“接受”要么“拒绝”这个输入。如果停止于“接受状态”，则自动机“接受”了这个字。在另一方面，如果它停止于“拒绝状态”，则这个字被“拒绝”。自动机接受的所有字的集合被称为“这个自动机接受的语言”。

但要注意，自动机一般不必须有有限数目甚至可数个状态。比如，量子有限自动机有不可数无限个状态，因为所有可能状态的集合是在复投影空间中所有点的集合。所以，量子有限自动机和有限状态机一样，都是更一般想法拓扑自动机的特殊情况，它的状态的集合是拓扑空间，而状态转移函数取自在这个空间上的所有可能函数。拓扑自动机经常叫做 M-自动机，简单是半自动机加上接受状态集合的补充，这里的集合交集确定初始状态是被接受还是被拒绝。

一般的说，自动机不需要严格的接受或拒绝一个输入；它可以按某个在零和一之间的概率接受它。还是用量子有限自动机作为展示例子，它只按某个概率接受输入。这个想法也是更一般情况几何自动机或度量自动机的特殊情况，它的状态的集合是度量空间，一个语言被这个自动机接受如果在初始点和接受状态的集合之间的距离关于这个度量是足够的小。

术语

自动机有如下基本概念：

形式描述

自动机 可以表示为5-元组 〈 〈 --> Q , Σ Σ --> , δ δ --> , q 0 , F 〉 〉 --> {\displaystyle \langle Q,\Sigma ,\delta ,q_{0},F\rangle } ，这里的:

Q 是 状态 的集合。

∑ 是符号的有限集合，我们称为这个自动机接受的语言的 字母表 。

δ 是 转移函数 ，就是

q 0 是 开始状态 ，就是说自动机在还未处理输入的时候的状态(明显的 q 0 ∈ Q)。

F 是叫做 终止状态 的 Q 中的状态的集合(就是 F⊆Q)。

给定一个输入字母 a ∈ ∈ --> Σ Σ --> {\displaystyle a\in \Sigma } ，可以使用简单的currying技巧写转移函数为 δ δ --> a : Q → → --> Q {\displaystyle \delta _{a}:Q\rightarrow Q} ，就是说，写 δ δ --> ( q , a ) = δ δ --> a ( q ) {\displaystyle \delta (q,a)=\delta _{a}(q)} 对于所有 q ∈ ∈ --> Q {\displaystyle q\in Q} 。这种方式下转移可以被更简单的看待: 它就是“动作”于 Q 中一个状态上的生成另一个状态的某种东西。你可以接着考虑重复的应用函数复合于各种函数 δ δ --> a {\displaystyle \delta _{a}} , δ δ --> b {\displaystyle \del幺半群_{b}} 等等的结果。重复的函数复合形成一个幺半群。对于转移函数，这个幺半群叫做转移幺半群，有时也叫做“变换半群”。

给定一对字母 a , b ∈ ∈ --> Σ Σ --> {\displaystyle a,b\in \Sigma } ，可以通过坚持 δ δ --> ^ ^ --> a b = δ δ --> a ∘ ∘ --> δ δ --> b {\displaystyle {\widehat {\delta }}_{ab}=\delta _{a}\circ \delta _{b}} 定义一个新函数 δ δ --> ^ ^ --> {\displaystyle {\widehat {\delta }}} ，这里的 ∘ ∘ --> {\displaystyle \circ } 指示函数复合。明显的，可以递归的继续这个过程，这样就有了为所有字 w ∈ ∈ --> Σ Σ --> ∗ ∗ --> {\displaystyle w\in \Sigma ^{*}} 定义的函数 δ δ --> ^ ^ --> w {\displaystyle {\widehat {\delta }}_{w}} 的递归定义，因此有了映射

这个构造也可以反过来: 给定 δ δ --> ^ ^ --> {\displaystyle {\widehat {\delta }}} ，可以重新构造一个 δ δ --> {\displaystyle \delta } ，因此两个描述是等价的。

三元组 〈 〈 --> Q , Σ Σ --> , δ δ --> 〉 〉 --> {\displaystyle \langle Q,\Sigma ,\delta \rangle } 被称为半自动机。半自动机位于自动机底下，它们就是忽略了开始状态和接受状态的自动机。开始状态和接受状态的补充概念允许自动机做半自动机不能形式语言: 它们可以识别形式语言。确定有限自动机 〈 〈 --> Q , Σ Σ --> , δ δ --> , q 0 , F 〉 〉 --> {\displaystyle \langle Q,\Sigma ,\delta ,q_{0},F\rangle } 接受的语言 L {\displaystyle L} 是:

就是说，一个自动机所接受的语言是在字母表 Σ Σ --> {\displaystyle \Sigma } 之上所有字 w 的集合，当给定为自动机的输入的时候，将导致它停止于 F {\displaystyle F} 中的某个状态。被自动机接受的语言叫做可识别语言。

当状态集合 Q 是有限的时候，自动机被称为有限状态自动机，而所有可识别的语言是正则语言。事实上，有一个强等价: 对于所有正则语言，都有一个有限状态自动机，反之亦然。

如上所述，集合 Q 不必须是有限或可数的；它可以采用一般的拓扑空间；这就得到了一般的拓扑自动机。另一种可能的推广是度量自动机或“几何自动机”。在这种情况下，改变了对语言的接受: 替代在 δ δ --> ^ ^ --> ( q 0 , w ) ∈ ∈ --> F {\displaystyle {\widehat {\delta }}(q_{0},w)\in F} 中的最终状态的集合包含，以在最终状态 δ δ --> ^ ^ --> ( q 0 , w ) {\displaystyle {\widehat {\delta }}(q_{0},w)} 和集合 F {\displaystyle F} 之间的度量距离的方式给出。特定类型的概率自动机是度量自动机，其度量空间是在概率空间上的测量。

有限自动机的分类

下面是三类有限自动机

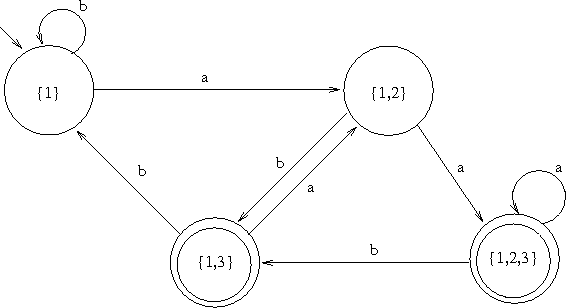
DFA

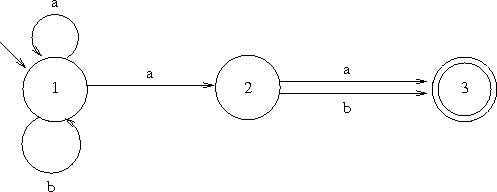
等价于前面例子 DFA 的 NFA

尽管可以证明所有这些自动机都“可以接受同样的语言”。你总是可以构造接受与给定的 NFA M 同样语言的某个 DFA M。

有限自动机的扩展

上述自动机接受的语言家族被称为正则语言家族。更强力的自动机可以接受更复杂的语言。比如:

有限状态自动机的最小化

根据Myhill-Nerode定理，在同构意义下接受一个正则语言的最少状态的确定有限状态自动机是唯一的。同时我们还存在有效的算法（时间开销是O(n )的）构造出与给定确定有限状态自动机等价的最小化的确定有限状态自动机。

计算能力与判定问题

确定有限状态自动机与非确定有限状态自动机识别的语言都是正则语言。由于正则语言的良好性质，许多为其他自动机（下推自动机或图灵机）不能判定的问题，在有限状态自动机的情形下，都可以得到判定，并且存在有效的算法。

对一个确定有限状态自动机，下述判定问题都可以判定，并且存在有效的算法。

该自动机识别的语言是否为空集。

该自动机识别的语言是否为有限集。

该自动机是否与另一个确定有限状态自动机识别同一个的语言。

引用

John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman - Introduction to Automata Theory, Languages, and Computation (2nd Edition)

Michael Sipser. Introduction to the Theory of Computation. PWS Publishing. 1997. ISBN 0-534-94728-X. Part One: Automata and Languages, chapters 1–2, pp.29–122. Section 4.1: Decidable Languages, pp.152–159. Section 5.1: Undecidable Problems from Language Theory, pp.172–183.

参见

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。