语法

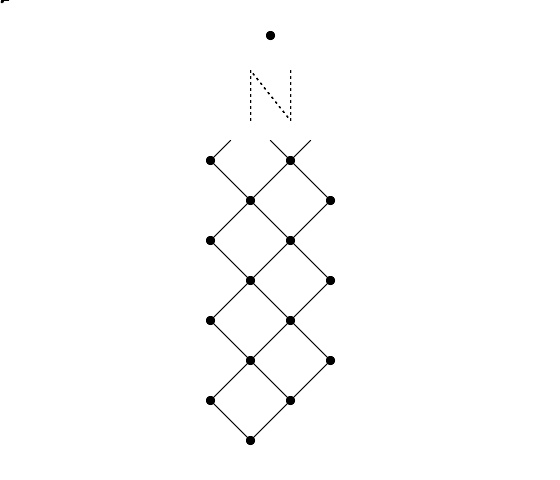
Rieger-Nishimura 格。它的节点是不别直觉逻辑等价之异的一元命题公式，按直觉逻辑蕴含排序。

直觉逻辑的公式的语法类似于命题逻辑或一阶逻辑。但是直觉逻辑的连结词不像经典逻辑那样是可互定义的，因此它们的选择是重要的。在直觉命题逻辑中通常使用 →, ∧, ∨, ⊥ 作为基本连结词，把 ¬ 作为 ¬A = (A → ⊥) 的简写处理。在直觉一阶逻辑中量词 ∃, ∀ 都是需要的。

不同在于很多经典逻辑的重言式在直觉逻辑中不再是可证明的。例子不只包括排中律P ∨ ¬P，还有皮尔士定律((P → Q) → P) → P，甚至还有双重否定除去。在经典逻辑中，P → ¬¬P 和 ¬¬P → P 二者都是定理。在直觉逻辑中，只有前者是定理: 双重否定可以介入但不能除去。

对很多经典有效重言式不是直觉逻辑的定理的观察导致了弱化经典逻辑的证明论的想法。

相继式演算

根岑发现简单限制他的系统LK（他的经典逻辑的相继式演算）就导致了关于直觉逻辑的一个可靠和完备的系统。他称之为系统LJ。

希尔伯特式演算

推理规则是肯定前件，公理有:

THEN-1: φ → (χ → φ)

THEN-2: (φ → (χ → ψ)) → ((φ → χ) → (φ → ψ))

AND-1: φ ∧ χ → φ

AND-2: φ ∧ χ → χ

AND-3: φ → (χ → (φ ∧ χ))

OR-1: φ → φ ∨ χ

OR-2: χ → φ ∨ χ

OR-3: (φ → ψ) → ((χ → ψ) → (φ ∨ χ → ψ))

NOT-1: (φ → χ) → ((φ → ¬χ) → ¬ φ)

NOT-2: φ → (¬φ → χ)

对于一阶逻辑系统还要加上普遍化规则，和如下公理:

PRED-1: (∀xZ(x)) → Z(t)

PRED-2: Z(t) → (∃xZ(x))

PRED-3: (∀x (W → Z(x))) → (W → ∀xZ(x))

PRED-4: (∀x (Z(x) → W)) → (∃xZ(x) → W)

算子的不可互定义性

在经典命题逻辑中，有可能选取合取、析取或蕴涵中的一个作为原始的，并依据它和否定来定义另两个，比如在扬·武卡谢维奇的命题逻辑三公理中。甚至可以依据自足算子比如皮尔士箭头(NOR)或Sheffer竖线(NAND)定义它们四个。类似的，在经典一阶逻辑中，一个量词可以依据另一个量词和否定来定义。

这是二值原理的推论，它使得这种连结词仅仅是布尔函数。二值原理在直觉逻辑中不成立，只有无矛盾律成立。作为结果没有连结词可以豁免，而上述公理都是必须的。多数经典恒等式只是直觉逻辑中在一个方向上的定理，尽管某些定理是两个方向的。它们如下:

合取与析取:

(ϕ ϕ -->∧ ∧ -->ψ ψ -->)→ → -->¬ ¬ -->(¬ ¬ -->ϕ ϕ -->∨ ∨ -->¬ ¬ -->ψ ψ -->){\displaystyle (\phi \wedge \psi )\to \neg (\neg \phi \vee \neg \psi )}

(ϕ ϕ -->∨ ∨ -->ψ ψ -->)→ → -->¬ ¬ -->(¬ ¬ -->ϕ ϕ -->∧ ∧ -->¬ ¬ -->ψ ψ -->){\displaystyle (\phi \vee \psi )\to \neg (\neg \phi \wedge \neg \psi )}

(¬ ¬ -->ϕ ϕ -->∨ ∨ -->¬ ¬ -->ψ ψ -->)→ → -->¬ ¬ -->(ϕ ϕ -->∧ ∧ -->ψ ψ -->){\displaystyle (\neg \phi \vee \neg \psi )\to \neg (\phi \wedge \psi )}

(¬ ¬ -->ϕ ϕ -->∧ ∧ -->¬ ¬ -->ψ ψ -->)↔ ↔ -->¬ ¬ -->(ϕ ϕ -->∨ ∨ -->ψ ψ -->){\displaystyle (\neg \phi \wedge \neg \psi )\leftrightarrow \neg (\phi \vee \psi )}

合取与蕴涵:

(ϕ ϕ -->∧ ∧ -->ψ ψ -->)→ → -->¬ ¬ -->(ϕ ϕ -->→ → -->¬ ¬ -->ψ ψ -->){\displaystyle (\phi \wedge \psi )\to \neg (\phi \to \neg \psi )}

(ϕ ϕ -->→ → -->ψ ψ -->)→ → -->¬ ¬ -->(ϕ ϕ -->∧ ∧ -->¬ ¬ -->ψ ψ -->){\displaystyle (\phi \to \psi )\to \neg (\phi \wedge \neg \psi )}

(ϕ ϕ -->∧ ∧ -->¬ ¬ -->ψ ψ -->)→ → -->¬ ¬ -->(ϕ ϕ -->→ → -->ψ ψ -->){\displaystyle (\phi \wedge \neg \psi )\to \neg (\phi \to \psi )}

(ϕ ϕ -->→ → -->¬ ¬ -->ψ ψ -->)↔ ↔ -->¬ ¬ -->(ϕ ϕ -->∧ ∧ -->ψ ψ -->){\displaystyle (\phi \to \neg \psi )\leftrightarrow \neg (\phi \wedge \psi )}

析取与蕴涵:

(ϕ ϕ -->∨ ∨ -->ψ ψ -->)→ → -->(¬ ¬ -->ϕ ϕ -->→ → -->ψ ψ -->){\displaystyle (\phi \vee \psi )\to (\neg \phi \to \psi )}

(¬ ¬ -->ϕ ϕ -->∨ ∨ -->ψ ψ -->)→ → -->(ϕ ϕ -->→ → -->ψ ψ -->){\displaystyle (\neg \phi \vee \psi )\to (\phi \to \psi )}

¬ ¬ -->(ϕ ϕ -->→ → -->ψ ψ -->)→ → -->¬ ¬ -->(¬ ¬ -->ϕ ϕ -->∨ ∨ -->ψ ψ -->){\displaystyle \neg (\phi \to \psi )\to \neg (\neg \phi \vee \psi )}

¬ ¬ -->(ϕ ϕ -->∨ ∨ -->ψ ψ -->)↔ ↔ -->¬ ¬ -->(¬ ¬ -->ϕ ϕ -->→ → -->ψ ψ -->){\displaystyle \neg (\phi \vee \psi )\leftrightarrow \neg (\neg \phi \to \psi )}

全称量词与存在量词:

(∀ ∀ -->x ϕ ϕ -->(x))→ → -->¬ ¬ -->(∃ ∃ -->x ¬ ¬ -->ϕ ϕ -->(x)){\displaystyle (\forall x\ \phi (x))\to \neg (\exists x\ \neg \phi (x))}

(∃ ∃ -->x ϕ ϕ -->(x))→ → -->¬ ¬ -->(∀ ∀ -->x ¬ ¬ -->ϕ ϕ -->(x)){\displaystyle (\exists x\ \phi (x))\to \neg (\forall x\ \neg \phi (x))}

(∃ ∃ -->x ¬ ¬ -->ϕ ϕ -->(x))→ → -->¬ ¬ -->(∀ ∀ -->x ϕ ϕ -->(x)){\displaystyle (\exists x\ \neg \phi (x))\to \neg (\forall x\ \phi (x))}

(∀ ∀ -->x ¬ ¬ -->ϕ ϕ -->(x))↔ ↔ -->¬ ¬ -->(∃ ∃ -->x ϕ ϕ -->(x)){\displaystyle (\forall x\ \neg \phi (x))\leftrightarrow \neg (\exists x\ \phi (x))}

所以，例如 “a 或 b”是比“如果非 a 则 b”更强的陈述，而在经典逻辑中它们是可互换的。

据 Alexander Kuznetsov 的证明，任一下述定义的连结词可以充当直觉逻辑的自足算子:

((p∨ ∨ -->q)∧ ∧ -->¬ ¬ -->r)∨ ∨ -->(¬ ¬ -->p∧ ∧ -->(q↔ ↔ -->r)),{\displaystyle ((p\lor q)\land \neg r)\lor (\neg p\land (q\leftrightarrow r)),}

p→ → -->(q∧ ∧ -->¬ ¬ -->r∧ ∧ -->(s∨ ∨ -->t)).{\displaystyle p\to (q\land \neg r\land (s\lor t)).}

语义

语义要比经典逻辑更加复杂。其模型论可给出自海廷代数或等价的给出自克里普克语义。

海廷代数语义

在经典逻辑中，我们经常讨论一个公式可能接受的真值。这种值通常被选择为布尔代数的成员。在布尔代数中的交和并算子等同于∧和∨逻辑连结词，所以形如A ∧ B的公式是在布尔代数中A的值和B的值的交。所以我们就有了一个有用的定理，一个公式是经典逻辑的有效的句子/断定，当且仅当它的值对于任何赋值都是1---就是说，对它的变量的任何指派都是真。

对于直觉逻辑对应的法则也是真的，但是不再对每个公式指派（assign）来自布尔代数的值，而是使用来自海廷代数的值，布尔代数是它的特殊情况。公式在直觉逻辑中是有效的，当且仅当它对于在任何海廷代数上的任何赋值总是得到值1。

可以证实为了识别有效的公式，考虑其元素是实平面R的开集的一个单一的Heyting代数就足够了。在这种代数中，∧和∨算子对应于集合的交集和并集，并且指派给公式A→B的值是 (A ∪ B)，它是B的值和A的值的补集的并集的内部。底元素是ø，顶元素是整个平面R。¬A定义为A→ø，所以指派给它的值是A，这是A的值的补集的内部。通过这些指派，直觉上有效的公式正好就是被指派为整个平面的值的公式。

例如，公式¬(A ∧ ¬A)是有效的，因为不管为公式A选择什么集合X作为值，¬(A ∧ ¬A)的值总是被证实为整个平面：

一个拓扑学定理告诉我们X°是X的子集，所以交集为空，因此：

所以这个公式的赋值是真，这个公式确实是有效的。

但是排中律A∨¬A，可以被证实是“无效的”，通过设定A的值是{y : y > 0 }。那么¬A的值是{y : y ≤ 0 }的内部，它就是{y : y 0 }和{y : y < 0 }的并集，这“不”是整个平面。

上面描述的无限海廷代数对所有直觉上有效的公式给出了真赋值，而不管为公式中的变量指派了什么值。反过来说，对于每个无效的公式，都有来对变量的来自这个代数的一个值指派生成这个公式的一个假赋值。可以证实没有有限的海廷代数有这个性质。

克里普克语义

建立在他关于模态逻辑的语义的工作之上，索尔·阿伦·克里普克为直觉逻辑建立了另一套语义，叫做克里普克语义或关系语义。

参见

直觉主义

BHK释义

直觉类型论

经典逻辑

中间逻辑

线性逻辑

构造性证明

Curry-Howard对应

可计算性逻辑

博弈语义

引用

Van Dalen, Dirk, 2001, "Intuitionistic Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.

Morten H. Sørensen, Pawel Urzyczyn, 2006, Lectures on the Curry-Howard Isomorphism (chapter 2: "Intuitionistic Logic"). Studies in Logic and the Foundations of Mathematics vol. 149, Elsevier.

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。