正六边形

正六边形是每条边等长、每个角相等的六边形，在施莱夫利符号中可以用 {6} 来表示 。正六边形亦可以将正三角形透过截角变换来构造，即切去正三角形的三个顶点，因此正六边形在施莱夫利符号中亦可以写为 t{3} 。但若截角深度太深或太浅都会产生一种具有两个不同边长的六边形。

一个利用尺规作图构造正六边形的逐步动画，这个方法由欧几里得的几何原本第四卷第15章给出 。六边形之所以为可作图多边形是因为边长 6 = 2 × × --> 3 {\displaystyle 6=2\times 3}

，是2个费马数的乘积。若已给定六边形的其中一边 AB 的边长，就分别以A和B为圆心、半径 AB 画弧，其交点M就是这个正六边形的外接圆圆心。画出外接圆后依序将 AB 线段复制到到圆周上，则可以绘制出正六边形 

正六边形是一个同时具有边可递和点可递特性的六边形，是一种 双心多边形 （ 英语 ： Bicentric polygon ） ，这意味着它同时具有内切圆和外接圆。

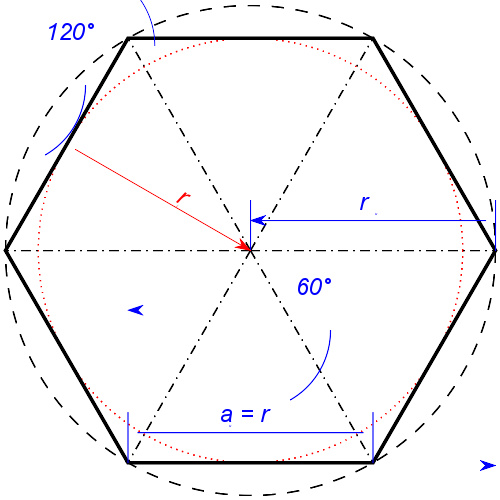
正六边形边的长度与其外接圆半径相等，且等于边心距的 2 3 3 {\displaystyle {\tfrac {2{\sqrt {3}}}{3}}} 倍，其中，边心距与内切圆半径相等。正六边形的每个内角都是120度，且具有6次的旋转对称性（阶数为6的旋转对称性）和6轴对称性（有6个对称轴的轴对称性），组成了D 6 二面体群的对称性。正六边形最长的对角线是两侧顶点的对角线，其长度恰好为边长的两倍，因此若有一个三角形其中一个顶点位于六边形几何中心、其中一条边与六边形共用，则这个三角形是正三角形，且正六边形可以分割成6个此三角形。

正六边形是其中一种能够密铺平面的正多边形，其余两种为正三角形和正方形。如同正方形和正三角形一样，正六边形可以经过重复的排列和组合，形成没有空隙或重叠的几何图形，这种图行每个顶点都是3个六边形的公共顶点，并形成一个很紧密的二维空间充填，也因此大部分的蜂窝都会将其的每个蜂房做成六边形，使其能够有效地利用空间和建材 。另外，正三角形镶嵌的沃罗诺伊图是正六边形镶嵌。虽然具有等边的特性，但并不常被当作 等边多边形 （ 英语 ： Equilateral polygon ） 。

参数

 

 

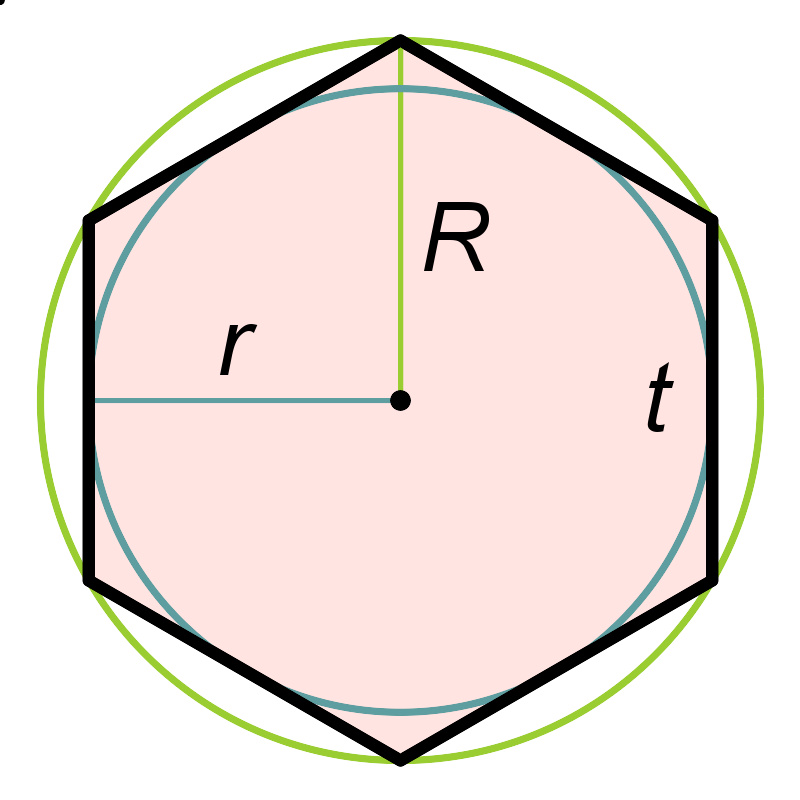
正六边形的最大直径D是最大半径或外接圆半径R的两倍，其外接圆半径R与边长t等长。

正六边形的面积为：

也可以利用其边心距套用任意正多边形公式求得：

正六边形可以单单用圆规直尺绘画。因为当正六边形内接于圆时，圆的半径刚好等于正六边形的边长，正六边形最长的对角线就等于圆的直径。中国古代对圆周和直径的关系有“周三径一”之说，可以视为采用正六边形为圆的近似图形求得的结果。

正六边形尺规作图

下面是正六边形的尺规作图，共三步。

画一条水平线，通过此线上的任意点做一个圆。

以该圆与线的交点为圆心，分别画出与该圆半径相同的圆，与该圆交于4点。

依顺序联结这4个点和该圆与水平线的交点即成正六边形。

面积

正六边形

因为正六边形由六个等边三角形组成，所以：

正六边形的面积=三角形面积×6= 3 4 × × --> a 2 × × --> 6 = 3 2 a 2 3 {\displaystyle {\frac {\sqrt {3}}{4}}\times a^{2}\times 6={\frac {3}{2}}a^{2}{\sqrt {3}}}

这些等边三角形的高是正六边形内切圆的半径，即 3 2 a {\displaystyle {\frac {\sqrt {3}}{2}}a} 。

六边形的密铺平面

有多种六边形可以密铺平面

扭歪六边形

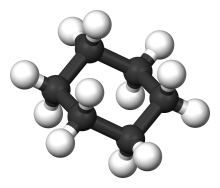
 环己烷的化学结构，碳原子的位置形成了一个扭歪六边形

扭歪六边形，又称不共面六边形，是指顶点并非完全共面的六边形

皮特里多边形

一些正扭歪六边形来自于高为多胞体的皮特里多边形。

多面体的截面

部分多面体具有六边形的截面，例如立方体 、正八面体 和正十二面体 。在立方体中，六边形的截面穿过对边的中点 。

自然中的六边形

苯

石墨

龟壳

自然地面龟裂

结晶体如冰

蜂巢的形状

雪花

参考文献

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。