简介

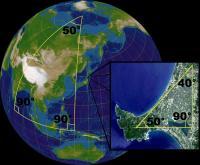
  理想化的地球是一个流形。越近看就越近似于平面（“大三角形”是曲边的，但右下角非常小的三角形就和平面上一样了）。

流形可以视为近看起来象欧几里得空间或其他相对简单的空间的物体。例如，人们曾经以为地球是平的。这是因为相对于地球来说人类实在太小，平常看到的地面是地球表面微小的一部分。所以，尽管知道地球实际上差不多是一个圆球，如果只需要考虑其中微小的一部分上发生的事情，比如测量操场跑道的长度或进地产交易时，仍然把地面看成一个平面。一个理想的数学上的球面在足够小的区域上的特性就像一个平面，这表明它是一个流形。但是球面和平面的整体结构是完全不同的：如果在球面上沿一个固定方向走，最终会回到起点，而在一个平面上，可以一直走下去。

回到地球的例子。像旅行的时候，会用平面的地图来指示方位。如果将整个地球的各个地区的地图合订成一本地图集，那么在观看各个地区的地图后，就可以在脑海中“拼接”出整个地球的景貌。为了能让阅读者顺利从一张地图接到下一张，相邻的地图之间会有重叠的部分，以便在脑海里“粘合”两张图。类似地，在数学中，也可以用一系列“地图”（称为坐标图或坐标卡）组成的“地图集”（atlas, 亦称为图册）来描述一个流形。而“地图”之间重叠的部分在不同的地图里如何变换，则描述了不同“地图”的相互关系。

描述一个流形往往需要不止一个“地图”，因为一般来说流形并不是真正的欧几里得空间。举例来说，地球就没法用一张平面的地图来合适地描绘。

流形要求局部“看起来像”简单的空间，这不是一个简单的要求。例如，在球上吊一根线，这个整体就不是一个流形。包含了线和球连接的那一点的附近区域一定不是简单的：既不是线也不是面，无论这个区域有多小。

流形有很多种。最简单的是拓扑流形，它们局部看来像欧几里得空间。其他的种类包含了它们在使用中所需要的额外的结构。例如，一个微分流形不仅支持拓扑，而且要支持微积分。黎曼流形的思想导致了广义相对论的数学基础，使得人们能够用曲率来描述时空。

引例：圆圈

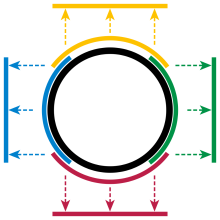
  四张图分别把圆的一部分映射到一个开区间，它们合在一起覆盖了整个圆。

圆是除欧几里得空间外的拓扑流形的一个简单例子。考虑一个半径为1，圆心在原点的圆。若 x {\displaystyle x} 和 y {\displaystyle y} 是圆上的点的坐标，则有 x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} 。

局部看来，圆像一条线，而线是一维的。换句话说，只要一个坐标就可以在局部描述一个圆。例如，圆的上半部， y {\displaystyle y} 坐标大于零的部分（右图中黄色的部分），任何一点都可以用 x {\displaystyle x} 坐标确定。投影映射：

把上半圆映射到开区间 ( − − --> 1 , 1 ) {\displaystyle (-1,1)} 。反过来，给定一个 x {\displaystyle x} ， ( x , 1 − − --> x 2 ) {\displaystyle (x,{\sqrt {1-x^{2}}})} 就是上半圆的一点：

这样的一个映射 ϕ ϕ --> top {\displaystyle \phi _{\mbox{top}}} 就是一个坐标图。它的作用，就是告诉读者“地图”上的一点对应着实际中的哪一点。 ϕ ϕ --> top {\displaystyle \phi _{\mbox{top}}} 和它连续函数都是连续函数甚至是光滑函数，这样的映射也叫做同胚（微分）同胚。类似的，也可以为圆的下半部（红），左半部（蓝），右半部（绿）建立坐标图。这四个部分合起来覆盖了整个圆，这四个坐标图就组成了该圆的一个图册。

注意圆上部和右部的重叠部分，也就是位于圆上 x {\displaystyle x} 和 y {\displaystyle y} 坐标大于0的四分之一圆弧。两个坐标图 ϕ ϕ --> top {\displaystyle \phi _{\mbox{top}}} 和 ϕ ϕ --> right {\displaystyle \phi _{\mbox{right}}} 都将这部分双射到区间 ( 0 , 1 ) {\displaystyle (0,1)} 。这样就有一个从 ( 0 , 1 ) {\displaystyle (0,1)} 到它自己的双射 T {\displaystyle T} ：首先取 ( 0 , 1 ) {\displaystyle (0,1)} 上面一点 a {\displaystyle a} （黄色线段右半部分的点）黄色坐标图的逆映射到达圆上的对应点 ( a , 1 − − --> a 2 ) {\displaystyle (a,{\sqrt {1-a^{2}}})} ，再通过绿色坐标图映射到 ( 0 , 1 ) {\displaystyle (0,1)} 上:

映射 T {\displaystyle T} 称为坐标变换映射，它告诉读者一张”地图“上的点是如何对应到另一张“地图”上的相应的点，说明了两张地图之间的关系。

另一个图册

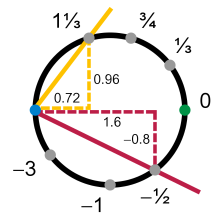
  圆圈流形基于斜率的坐标图集，每个图覆盖除了一点之外的所有点。

上，下，左，右四个坐标图表明圆是一个流形，但它们不是唯一可以描述圆形的图册。坐标图除了可以是几何投影，也可以是别的映射，而坐标图的数量也可以不是四个，只要能够覆盖整个圆就行了。考虑以下两个坐标图

这里 s {\displaystyle s} 是过点 ( x , y ) {\displaystyle (x,y)} 和固定点 ( − − --> 1 , 0 ) {\displaystyle (-1,0)} 之直线的斜率。比如右图中，点 ( − − --> 0.28 , 0.96 ) {\displaystyle (-0.28,0.96)} 和 ( − − --> 1 , 0 ) {\displaystyle (-1,0)} 确定的直线（右图黄色直线）斜率是 1 1 3 {\displaystyle 1{1 \over 3}} ；点 ( 0.6 , − − --> 0.8 ) {\displaystyle (0.6,-0.8)} 和 ( − − --> 1 , 0 ) {\displaystyle (-1,0)} 确定的直线（右图红色直线）的斜率则是 − − --> 1 2 {\displaystyle -{1 \over 2}} 。 ϕ ϕ --> m i n u s {\displaystyle \phi _{\mathrm {minus} }} 可以把圆上面除了点 ( − − --> 1 , 0 ) {\displaystyle (-1,0)} 以外的点一一映射到实数轴 ( − − --> ∞ ∞ --> , ∞ ∞ --> ) {\displaystyle (-\infty ,\infty )} 上。 ϕ ϕ --> p l u s {\displaystyle \phi _{\mathrm {plus} }} 则是 ϕ ϕ --> m i n u s {\displaystyle \phi _{\mathrm对称minus} }} 关于 y {\displaystyle y} 轴的镜像对称（也就是左右对称），固定点是 ( + 1 , 0 ) {\displaystyle (+1,0)} 。 ϕ ϕ --> m i n u s {\displaystyle \phi _{\mathrm {minus} }} 的逆映射为

很容易确认 x 2 + y 2 = 1 {\displaystyle x^{2}+y^{2}=1} 对于所有斜率值 s {\displaystyle s} 成立。这两个坐标图提供了圆圈的又一个图集，其变换函数为

注意每个坐标图都缺了一点，对于 s {\displaystyle s} 是点 ( − − --> 1 , 0 ) {\displaystyle (-1,0)} ，对于 t {\displaystyle t} 是点 ( + 1 , 0 ) {\displaystyle (+1,0)} ，所以每个坐标图不能独自覆盖整个圆圈。利用拓扑学的工具可以证明，没有单个的坐标图可以覆盖整个圆圈；在这个简单的例子里，已经可以看到流形拥有多个坐标图的灵活性。

  从代数曲线来的四个流形: ■ 圆圈, ■ 抛物线, ■ 双曲线, ■ 三次曲线.

流形不必连通（整个只有一片）;这样，一对分离的圆圈可以是一个流形。它们不必是闭的，所以不带两个端点的线段也是流形。它们也不必有限，这样抛物线也是一个流形。

定义

拓扑流形的数学定义可以表述为：

坐标图

一个流形的一个坐标映射,坐标图，或简称图是一个在流形的一个子集和一个简单空间之间的双射，使得该映射及其逆都保持所要的结构。对于拓扑流形，该简单空间是某个欧几里得空间R而一般感兴趣的是其拓扑结构。这个结构被同胚保持，也就是可逆的在两个方向都连续的映射。例如上节提到的映射 ϕ ϕ --> top {\displaystyle \phi _{\mbox{top}}} 是圆圈的一个图。图对于计算极其重要，因为它使得计算可以在简单空间进行，再把结果传回流形。

图册

多数流形的表述需要多于一个的图（只有最简单的流形只用一个图）。覆盖流形的一个特定的图的集合称为一个图册。图集不是唯一的，因为所有流形可以被不同的图的组合用很多方式覆盖。

包含所有和给定图集相一致的图的图集称为极大图册。不像普通的图集，极大图册是唯一的。虽然可能在定义中有用，这个对象非常抽象，通常不直接使用（例如，在计算中）。

坐标变换映射

图册中的图通常会互相重叠，而流形中的一个点可能会被好几个图所表示。如果两个图重叠，它们的部分会表示流形的同一个区域。这些部分之间的关联代表流形上同一点的坐标点的映射，譬如上面圆圈例子中的映射T，称为坐标变换,变换函数，或者转换函数,转换映射。

附加结构

图册也可用于定义流形上的附加结构。结构首先在每个图上分别定义。如果所有变换映射和这个结构相容，该结构就可以转到流形上。

这是微分流形的标准定义方式。如果图册的变换映射对于一个拓扑流形保持R自然的微分结构（也就是说，如果它们是微分同胚），该微分结构就传到了流形上并把它变成微分流形。

通常，流形的结构依赖于图册，但有时不同的图册给出相同的结构。这样的图册称为相容的。

构造

一个流形可以以不同方式构造，每个方式强调了流形的一个方面，因而导致了不同的观点。

图册构造

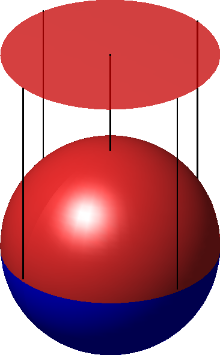
  该坐标图把球面有正z坐标的部分映射到一个圆盘。

构造一个流形的一个简单方法是在上面的例子中的圆圈的构造方法。首先，确认R的一个子集，然后覆盖这个子集的图册被构造出来。流形的概念历史上就是从这样的构造发展出来的。这里有另一个例子，把这个方法应用在球面的构造上:

带图册的球面

球面的表面可以几乎和圆圈一样的方法来处理。可把球面视作R的子集:

球面是二维的，所以每个坐标图将映射球面的一部分到一个R的开子集。例如考虑北半球，它是带正z坐标的部分。（在右图中它着红色）定义如下的函数χ

把北半球映射到开单位圆盘，通过把它投影到（x, y）平面。类似的坐标图对南半球也存在。和投影到（x, z）平面的两个坐标图以及投影到（y, z）平面的两个坐标图一起，就得到了一个覆盖整个球面的含6个坐标图的图册。

这可以很容易地扩展到高维的球面。

贴补

流形可以通过把碎片以一种相容的方式粘合来构造，使得碎片成为互相覆盖的坐标图。这种构造对于任何流形都是可行的，所以经常作为流形的表述，特别是微分和黎曼流形。它集中于图册的构造，把流形作为坐标图所自然的提供的贴片，因为不涉及外部的空间，这导致了流形的内在的观点。

这里，流形通过给定图册来构造，图册通过定义转换映射来得到。流形的一个点因而是指通过变换映射映到同一个点的坐标点的等价类。坐标图把等价类映射到一个贴片上的点。通常会对变换映射有很强的一致性要求。对于拓扑流形，它们被要求为同胚；如果它们也是微分同胚，最后得到的流形就是微分流形。

这可以通过变换映射圆圈例子的第二部分中的t = ⁄s来解释。从直线的两个拷贝开始。第一个拷贝用坐标s，第二个拷贝用t。现在，通过把第二个拷贝上的点t和第一个拷贝上的点⁄s作为同一个点来粘合起来(点t = 0不和任何第一个拷贝上的点认同)。这就给出了一个圆圈。

内在和外在的观点

第一种构造和这种构造非常相似，但是他们代表了相当不同的观点。在第一种构造中，流形被视为嵌入到某个欧几里得空间中。这是外在的观点。当一个流形用这种方式来看的时候，它很容易通过直觉从欧几里得空间得到附加的结构。例如，在欧几里得空间，很明显某个点的一个向量是否和穿过该点的曲面相切或者垂直。

贴补构造不用任何嵌入，只是简单把流形看作拓扑空间本身。这个抽象的观点称为内在的观点。这使得什么是切向量更难以想象。但是它表达了流形的本质，在计算上来讲，这可以避免使用更高的维数，例如只要二维而不是三维就可以作球面上的计算。

作为贴补的n维球面

函数的零点

很多流形可以定义为某个函数的零点集。这个构造自然的把流形嵌入一个欧几里得空间，因而导向一个外在的观点。这很形象，但不幸的是不是每个流形都可以这样表示。

如果一个可微函数的雅可比矩阵在函数为0的每一点是满秩的，则根据隐函数定理，每个这样的点周围存在一个为0的领域微分同胚于一个欧几里得空间。因此零点集是一个流形。

作为一个函数零点的n维球面

黏合一个流形上的不同点

可以把流形上的不同点定义为相同。这可以视为把不同的点粘合为同一个点。这构造出的结果不保证是流形，但在有些情况下会是流形。

这些情况下，黏合过程是用群来完成的，这是作用在流形上的群。两个点被视为同一个如果一个能被该群的一个元素移动到另一个上面。如果M是该流形而G是该群，结果空间称为商空间，并记为M/G。可以通过黏合点来构造的流形包括环面和实射影空间（分别从一个平面和一个球面开始）。举例来说，假设 S 2 = { ( x , y ) ∈ ∈ --> R 2 ∣ ∣ --> x 2 + y 2 = 1 } , H = { e , g } , e , g : S 2 ↦ ↦ --> S 2 , e ( x ) = x , g ( x ) = − − --> x , ∀ ∀ --> x ∈ ∈ --> S 2 {\displaystyle S^{2}=\{(x,y)\in \mathbb {R} ^{2}\mid x^{2}+y^{2}=1\},H=\{e,g\},e,g:S^{2}\mapsto S^{2},e(x)=x,g(x)=-x,\,\forall x\in S^{2}} ， 则二维实射影空间 R P 2 = S 2 / H {\displaystyle \mathbb {R} P^{2}=S^{2}/H} 。

直积

流形的直积也是流形。但不是每个流形都是一个积。

积流形的维数是其因子的维数之和。其拓扑是乘积拓扑，而坐标图的直积是积流形的坐标图。这样，积流形的图册可以用其因子的图册构造。如果这些图册定义了因子上的微分结构，相应的积图册定义了积流形上的一个微分结构。因子上定义的其他结构也可以同样处理。如果一个因子有一个边界，积流形也有边界。直积可以用来构造环面和有限圆柱面，例如，分别定义它们为S × S和S × [0, 1]。

  有限圆柱面是带边界的流形。

沿边界粘合

两个带边界的流形可以沿着边界粘合。如果用正确的方式完成，结果也是流形。类似的，一个流形的两个边界也可以粘合起来。

形式化的，粘合可以定义为两个边界的一个双射。两个点被认同为一个，如果它们互相映射到对方。对于一个拓扑流形，这个双射必须是同胚，否则结果就不是拓扑流形。类似的，对于一个微分流形，它必须是微分同胚。对于其它流形，其他的结构必须被这个双射所保持。

有限的圆柱面可以作为一个流形构造，先从一个长条R × [0, 1]开始，然后把对边通过适当的微分同胚粘合起来。克莱因瓶可以由一个带孔的球面和一个莫比乌斯带沿着各自的圆形边界粘合起来得到。

拓扑流形

最容易定义的流形是拓扑流形，它局部看起来象一些“普通”的欧几里得空间R。形式化地讲，一个拓扑流形是一个局部同胚于一个欧几里得空间的拓扑空间。这表示每个点有一个邻域，它有一个同胚（连续双射其逆也连续）将它映射到R。这些同胚是流形的坐标图。

通常附加的技术性假设被加在该拓扑空间上，以排除病态的情形。可以根据需要要求空间是豪斯多夫的并且第二可数。这表示下面所述的有两个原点的直线不是拓扑流形，因为它不是豪斯朵夫的。

流形在某一点的维数就是该点映射到的欧几里得空间图的维数（定义中的数字n）。连通流形中的所有点有相同的维数。有些作者要求拓扑流形的所有的图映射到同一欧几里得空间。这种情况下，拓扑空间有一个拓扑不变量，也就是它的维数。其他作者允许拓扑流形的不交并有不同的维数。

微分流形

很容易定义拓扑流形，但是很难在它们上面工作。对于多数应用，拓扑流形的一种，微分流形比较好用。如果流形上的局部坐标图以某种形式相容，就可以在该流形上讨论方向，切空间，和可微函数。特别是，可以在微分流形上应用“微积分”。

可定向性

考虑一个拓扑流形，其坐标图映射到R。给定一个R的有序基，坐标图就给它所覆盖的流形的一片引入了一个方向，可以视为或者右手或者左手的。重叠的坐标图不要求在方向上一致，这给了流形一个重要的自由度。对于某些流形，譬如球面，可以选取一些坐标图使得重叠区域在"手性"上一致；这些流形称为"可定向"的。对于其它的流形，这不可能做到。后面这种可能性容易被忽视，因为任何在三维空间中（不自交的）嵌入的闭曲面都是可定向的。

考虑三个例子: (1)莫比乌斯带，它是有边界的流形，（2）克莱因瓶，它在三维空间必须自交，以及（3）实射影平面，它很自然的出现在几何学中。

  莫比乌斯带

莫比乌斯带

从一个竖着的无限圆柱面开始，这是一个无边界的流形。在高和低的地方各剪一刀，产生两个圆形边界，和它们之间的一个圆形的带子。这是一个带边界的可定向流形，若在它上面动一个小"手术"。把带子剪开，使得它能展开成一个矩形，但把两头捏住。把其中一头转180°，把内面翻倒朝外，然后把两头无缝的粘回来。现在有了一个永久半翻转的带子，就是莫比乌斯带。它的边界不再是一对圆圈，而是（拓扑上）单个圆圈；曾经是"内面"的现在和"外面"并了起来，使得它只有"单"面。（在打印机的色带中有这种左扭带的应用。）

克莱因瓶

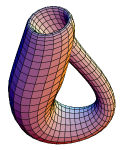
  嵌入到三维空间的克莱因瓶。

取两个莫比乌斯带；每个都以一个圈为边界。把每个圈拉成一个圆圈，并把带子变成交叉帽（cross-cap）。（注意这在三维空间物理上是不可能的；克莱因瓶不能放到三维空间中，就像莫比乌斯带（或者球面）不能放在平面上一样。实际建造一个克莱因瓶必需在至少四维的空间进行）把圆圈粘合起来会产生一个新的闭合流形，没有边界的克莱因瓶。把曲面闭合起来并不能改变不可定向性，它只是移除了边界。这样克莱因瓶就成了一个不能分辨内外的闭合曲面。

实射影平面

从圆心为原点的球面开始。穿过原点的每条直线在两个相对的点穿透球面。虽然在物理上不能这么做，但在数学上可以把相对点黏合为同一点。这样产生的闭合曲面是实射影平面，为一个不可定向曲面。它有一些等价的表述和构造，但是这个方法揭示了它的名字:所有给定的穿过原点的直线射影到该"平面"的一个"点"。

豪斯多夫假设

两个原点的线

这里给出一个空间的例子，它满足拓扑流形所有的条件，除了它不是豪斯多夫空间（Hausdorff space）。取两个R的拷贝，把它们写作

并定义如下等价关系

从这个等价关系得到的商空间L 是一个象实直线那样的空间， { ( x , 0 ) ∣ ∣ --> x ∈ ∈ --> R } {\displaystyle \{(x,0)\mid x\in \mathbb {R} \}} ，再加上额外的一点 ( 0 , 1 ) {\displaystyle (0,1)} 。特别的是， L {\displaystyle L} 上的 ( 0 , 0 ) {\displaystyle (0,0)} 和 ( 0 , 1 ) {\displaystyle (0,1)} 这两点不能被不相交的开集所分离，所以L不是豪斯多夫的。它是一个拓扑流形，但不是豪斯多夫拓扑流形。

经常，拓扑流形被定义为必须是豪斯多夫的，在这个定义下，上面的例子不是流形。

流形的其他类型和推广

要在流形上研究几何，通常必须用附加的结构来装饰这些空间，例如上面的微分流形所加入的微分结构。根据所需要的不同的几何，有许多其它的可能性:

复流形:复流形是建模在C上的流形，在坐标图的重叠处以全纯函数为变换函数。这些流形是复几何研究的基本对象。一个一维复流形称为黎曼曲面。

巴拿赫和Fréchet流形:要允许无穷维，可以考虑巴拿赫流形，它局部同胚于巴拿赫空间。类似的，Fréchet流形局部同胚于Fréchet space。

轨形（Orbifolds）:一个轨形是流形的推广，允许某种"奇异点"在其拓扑中存在。大致来讲，它是局部看起来像一些简单空间（例如，欧几里得空间）通过各种有限群的群作用的商。奇点对应于群作用的不动点，而作用必须在某种意义下相容。

代数簇和概形（Algebraic varieties and schemes）:一个代数簇是几个仿射代数簇粘起来得到的，仿射代数簇是在代数封闭的域上多项式的零点集。类似的，概形是仿射概形粘起来得到的，而仿射概形是代数簇的一个推广。二者都和流形相关，但都使用层而非坐标图集来构造。

历史

第一个清楚地把曲线和曲面本身构想为空间的可能是高斯，他以他的“绝妙定理”（Theorema egregium）建立了内在的微分几何。

黎曼是第一个广泛的展开真正需要把流形推广到高维的工作的人。流形的名字来自黎曼原来的德语术语Mannigfaltigkeit，William Kingdon Clifford把它翻译为"manifoldness"（多层）。在他的哥廷根就职演说中，黎曼表明一个属性可以取的所有值组成一个Mannigfaltigkeit。他根据值的变化连续与否对stetige Mannigfaltigkeit和离散 [sic] Mannigfaltigkeit（连续流形 和不连续流形）作了区分。作为stetige Mannigfaltikeiten的例子，他提到了物体颜色和在空间中的位置，以及一个空间形体的可能形状。他把一个n fach ausgedehnte Mannigfaltigkeit（n次扩展的或n-维流形）构造为一个连续的（n-1）fach ausgedehnte Mannigfaltigkeiten堆。黎曼直觉上的Mannigfaltigkeit概念发展为今天形式化的流形。黎曼流形和黎曼曲面就是以他的名字命名的。

交换簇的概念在黎曼的时代已经被隐含地作为复流形使用。从几何方面考虑，拉格朗日力学和哈密尔顿力学的本质也是流形理论。

庞加莱研究了三维流形，并提出著名的庞加莱猜想：所有闭简单连通的三维流形同胚于3维球吗？这个猜想已被Grigori Perelman解决。

赫尔曼·外尔于1912年给出了微分流形的一个内在的定义。1930年代，该课题基础性方面的工作被Hassler Whitney等人厘清，使得从19世纪下半叶起开始发展起来的相关的直觉知识变得更精确，并通过微分几何和李群使微分流形的理论得到进一步的发展。

相关条目

坐标转换

豪斯多夫空间

坐标邻域

欧几里得空间

代数簇（algebraic variety，或称代数多样体）

概形

流形列表

曲面

3-流形

4-流形

参考文献

一般参考

Guillemin, Victor and Anton Pollack, Differential Topology, Prentice-Hall (1974) ISBN 978-0-13-212605-2. This text was inspired by Milnor, and is commonly used for undergraduate courses.

Hirsch, Morris, Differential Topology, Springer (1997) ISBN 978-0-387-90148-0. Hirsch gives the most complete account with historical insights and excellent, but difficult problems. This is the best reference for those wishing to have a deep understanding of the subject.

Kirby, Robion C.; Siebenmann, Laurence C. Foundational Essays on Topological Manifolds. Smoothings, and Triangulations. Princeton, New Jersey: Princeton University Press (1977). ISBN 978-0-691-08190-8. A detailed study of the category of topological manifolds.

Lee, John M. Introduction to Topological Manifolds, Springer-Verlag, New York (2000). ISBN 978-0-387-98759-0. Introduction to Smooth Manifolds, Springer-Verlag, New York (2003). ISBN 978-0-387-95495-0. Graduate-level textbooks on topological and smooth manifolds.

Milnor, John, Topology from the Differentiable Viewpoint, Princeton University Press, (revised, 1997) ISBN 978-0-691-04833-8. This short text may be the best math book ever written.

Spivak, Michael, Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. HarperCollins Publishers (1965). ISBN 978-0-8053-9021-6. This is the standard text used in most graduate courses.

Riemann, Bernhard,Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. The 1851 doctoral thesis in which "manifold" (Mannigfaltigkeit) first appears.

Riemann, Bernhard,On the Hypotheses which lie at the Bases of Geometry. The famous Göttingen inaugural lecture (Habilitationsschrift) of 1854.

Sharpe, R.W., Differential Geometry:Cartan"s Generalization of Klein"s Erlangen Program, Springer-Verlag, ISBN 978-0-387-94732-7.

Template:Tensors

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。