简介

两个粒子的相互作用量由反应截面积所量化，其大小取决于它们的碰撞，该相互作用发生的概率尤其重要。如果该相互作用的强度不太大（即是能够用摄动理论解决），这反应截面积（或更准确来说是对应的时间演变算子、分布函数或S矩阵）能够用一系列的项（戴森级数）所表示，这些项能描述一段短时间所发生的故事，像以下的例子：

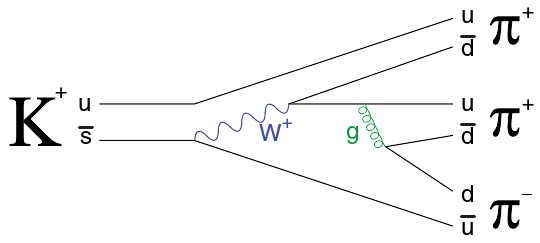
本图中，K介子（由一上夸克与反奇夸克组成）在弱相互作用下衰变成三个π介子，中间步骤有W玻色子及胶子参与。

两个具有一定相对速度的粒子在自由地移动（由两条向着大致方向的线表示）

它们遇到对方（两线连于第一点──顶点）

它们在同一路径上漫步（两线合二为一）

然后再度分开（第二个顶点）

但它们发觉自己的速度已变，而且再也不和之前一样（两线从最后的顶点向上──有时样式会因应粒子所经历的转变而有所不同）

这故事能够以图来表示，这一般来说要比记起对应戴森级数的数学公式要容易得多。这种图被称为费恩曼图。它们在戴森级数迅速趋向极限时才有意义。由于它们能够说简易的故事，而且又跟早期的气泡室实验相似，所以费恩曼图变得非常普及。

动机与历史

粒子物理学中，计算散射反应截面积的难题简化成加起所有可能存在的居间态振幅（每一个对应摄动理论又称戴森级数的一个项）。用费恩曼图表示这些状态以，比了解当年冗长计算容易得多。从该系统的基础拉格朗日量能够得出费恩曼法则，费恩曼就是用该法则表明如何计算图中的振幅。每一条内线对应虚粒子的分布函数；每一个线相遇顶点给出一个因子和来去的两线，该因子能够从相互作用项的拉格朗日量中得出，而线则约束了能量、动量和自旋。费恩曼图因此是出现在戴森级数每一个项的因子的符号写法。

但是，作为微扰的展开式，费恩曼图不能包含非微扰效应。

除了它们在作为数学技巧的价值外，费恩曼图为粒子的相互作用提供了深入的科学理解。粒子会在每一个可能的方式下相互作用：实际上，居间的虚粒子超越光速是允许的。（这是基于测不准原理，因深奥的理由而不违反相对论；事实上，超越光速对保留相对性时空的偶然性有帮助。）每一个终态的概率然后就从所有如此的概率中得出。这跟量子力学的泛函积分表述有密切关系，该表述（路径积分）也是由费曼发明的。

如此计算如果在缺少经验的情况下使用，通常会得出图的振幅为无穷大，这个答案在物理理论中是不能接受的。问题在于粒子自身的相互作用被错误地忽视了。重整化的技巧（是由费曼、施温格和朝永所开发的）弥补了这个效应并消除了麻烦的无穷大项。经过这样的重整化后，用费曼图做的计算通常能与实验结果准确地吻合。

费恩曼图及路径积分法亦被应用于统计力学中。

其他名称

默里·盖尔曼一直将费恩曼图称为斯蒂克尔堡图(Stückelberg diagrams)，因为瑞士物理学家厄恩斯特·斯蒂克尔堡(Ernst Stückelberg)发明了一个相近的图 。

历史上他们也曾被叫成 费恩曼-戴森图 或 戴森图 。

例子

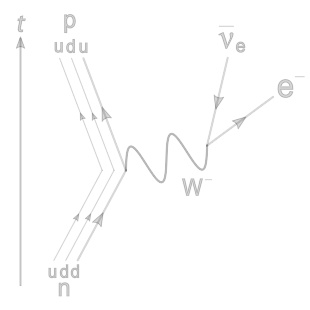
β衰变

右图为β衰变的费曼图。图中的直线代表费米子，而波浪线则代表虚玻色子。在本例中，图被设定在流形时空中，y坐标为时间而x坐标为空间；x坐标亦代表了某些相互作用（考虑 碰撞 ）的“地点”。由于时间朝着y轴方向，所以中微子是向着时间方向行进的；但费米子可以被视为其向时间后方移动的反粒子，因为数学上这两个概念没有分别。这适用于所有粒子和反粒子。

量子电动力学

在量子电动力学中，有两个场标记，叫“电子”和“光子”。“电子”有一定方向而“光子”无固定方向。当中只有一种相互作用，用“γ”标记，其三度分别为“光子”、“电子”“头”和“电子”“尾”。

参考资料

Gerardus "t Hooft, Martinus Veltman, Diagrammar , CERN Yellow Report 1973,online

David Kaiser, Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics , Chicago: University of Chicago Press, 2005. ISBN 0-226-42266-6

Martinus Veltman, Diagrammatica: The Path to Feynman Diagrams , Cambridge Lecture Notes in Physics, ISBN 0-521-45692-4 (expanded, updated version of above)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。