多鞍点函数积分

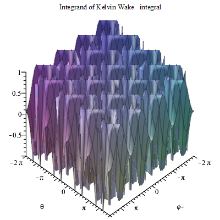
Integrand of Kelvin Wake Integral

Kelvin Ship Wake Integrand contour Maple plot

当船只以速度V驶过深水湖面，波形的幅度在相对于船只为静止的极坐标（ρ ρ -->,ϕ ϕ -->{\displaystyle \rho ,\phi }中在船只的速度矢量方向，ϕ ϕ -->=0{\displaystyle \phi =0}），由下列公式表示

K(ϕ ϕ -->,ρ ρ -->)=∫ ∫ -->− − -->π π -->/2π π -->/2cos(ρ ρ -->cos(θ θ -->+ϕ ϕ -->)cos2θ θ -->dθ θ -->{\displaystyle K(\phi ,\rho )=\int _{-\pi /2}^{\pi /2}cos(\rho {\frac {cos(\theta +\phi )}{cos^{2}\theta }}d\theta }

其中ρ ρ -->=gr/V2{\displaystyle \rho =gr/V^{2}}

1ρ ρ -->=V2gr{\displaystyle {\frac {1}{\rho }}={\frac {V^{2}}{gr}福禄数福禄数的平方Fr2{\displaystyle Fr^{2}}

g{\displaystyle g}为重力常数l{\displaystyle l}为船的长度。

上列K函数是下列多鞍点积分的正数部分：

K(ϕ ϕ -->,ρ ρ -->)=Re(∫ ∫ -->− − -->∞ ∞ -->∞ ∞ -->exp⁡ ⁡ -->(i∗ ∗ -->ρ ρ -->∗ ∗ -->f(θ θ -->,ρ ρ -->)dθ θ -->){\displaystyle K(\phi ,\rho )=Re(\int _{-\infty }^{\infty }\exp(i*\rho *f(\theta ,\rho )d\theta )} 其中，多鞍点积分的核函数为

f(θ θ -->,ϕ ϕ -->)=− − -->cos(θ θ -->+ϕ ϕ -->)cos2θ θ -->{\displaystyle f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}}

此核函数是一个多鞍点函数，振荡剧烈如图

求其极点，

df(θ θ -->,ϕ ϕ -->)dθ θ -->=sin(θ θ -->+ϕ ϕ -->)cos(θ θ -->)2− − -->2∗ ∗ -->cos(θ θ -->+ϕ ϕ -->)∗ ∗ -->sin(θ θ -->)cos(θ θ -->)3=0{\displaystyle {\frac {df(\theta ,\phi )}{d\theta }}={\frac {sin(\theta +\phi )}{cos(\theta )^{2}}}-{\frac {2*cos(\theta +\phi )*sin(\theta )}{cos(\theta )^{3}}}=0}

解之，得

θ θ -->1=arctan((1/4)∗ ∗ -->(1+(1− − -->8∗ ∗ -->tan(ϕ ϕ -->)2))tan(ϕ ϕ -->))=− − -->arctan((1/4)∗ ∗ -->(− − -->1+(1− − -->8∗ ∗ -->tan(ϕ ϕ -->)2))tan(ϕ ϕ -->)){\displaystyle \theta _{1}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})}

由此

ϕ ϕ -->1=19.47{\displaystyle \phi _{1}=19.47}度,

ϕ ϕ -->2=− − -->19.47{\displaystyle \phi _{2}=-19.47}度

这就是凯尔文船波的V型波包线的夹角，最早由凯尔文男爵发现，而且角度与船速无关.至于波纹本身则与船速矢量的夹角为

θ θ -->=π π -->− − -->19.47=35.3{\displaystyle \theta =\pi -19.47=35.3}°

开尔文驻相法

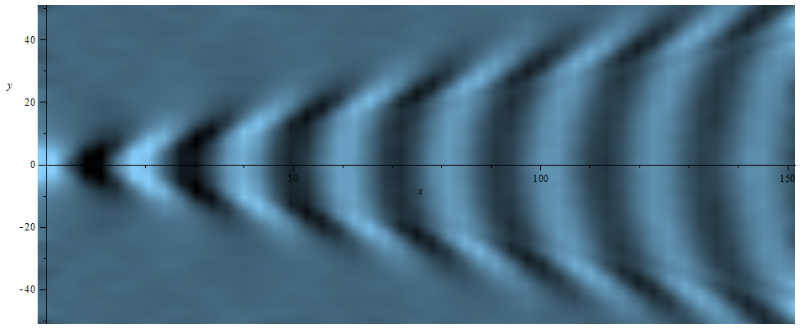
Kelvin Wake (Maple density plot)

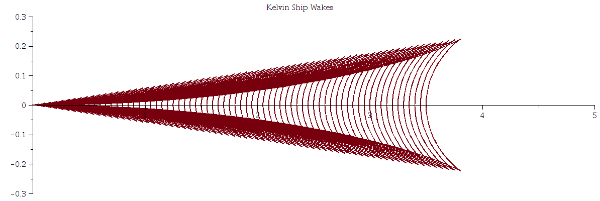
开尔文船波波形

开尔文船波积分K(ϕ ϕ -->,ρ ρ -->){\displaystyle K(\phi ,\rho )}必须通过数值积分计算。开尔文男爵根据被积分函数在积分区间内剧烈震荡的特点，提出了驻相法（Method of Stationary Phase）。

原理：当被积分函数剧烈震荡时，除了在极点外，震荡的被积分函数正负相抵消，因此可以将此被积分函数在极点的值作为整个积分的近似，驻相法乃是拉普拉斯方法的推广。

被积分函数 f(θ θ -->,ϕ ϕ -->)=− − -->cos(θ θ -->+ϕ ϕ -->)cos2θ θ -->{\displaystyle f(\theta ,\phi )=-{\frac {cos(\theta +\phi )}{cos^{2}\theta }}} 的两个极点是：

θ θ -->p=arctan((1/4)∗ ∗ -->(1+(1− − -->8∗ ∗ -->tan(ϕ ϕ -->)2))tan(ϕ ϕ -->)){\displaystyle \theta _{p}=arctan({\frac {(1/4)*(1+{\sqrt {(1-8*tan(\phi )^{2}))}}}{tan(\phi )}})}

θ θ -->m=− − -->arctan((1/4)∗ ∗ -->(− − -->1+(1− − -->8∗ ∗ -->tan(ϕ ϕ -->)2))tan(ϕ ϕ -->)){\displaystyle \theta _{m}=-arctan({\frac {(1/4)*(-1+{\sqrt {(}}1-8*tan(\phi )^{2}))}{tan(\phi )}})}

令

fm=f(θ θ -->m,ϕ ϕ -->)=sin((1/2)∗ ∗ -->ϕ ϕ -->− − -->(1/2)∗ ∗ -->arcsin(3∗ ∗ -->sin(ϕ ϕ -->)))sin((1/2)∗ ∗ -->ϕ ϕ -->+(1/2)∗ ∗ -->arcsin(3∗ ∗ -->sin(ϕ ϕ -->))){\displaystyle f_{m}=f(\theta _{m},\phi )={\frac {sin((1/2)*\phi -(1/2)*arcsin(3*sin(\phi )))}{sin((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}}

fp=f(θ θ -->p,ϕ ϕ -->)=cos((1/2)∗ ∗ -->ϕ ϕ -->+(1/2)∗ ∗ -->arcsin(3∗ ∗ -->sin(ϕ ϕ -->)))cos(− − -->(1/2)∗ ∗ -->ϕ ϕ -->+(1/2)∗ ∗ -->arcsin(3∗ ∗ -->sin(ϕ ϕ -->))){\displaystyle f_{p}=f(\theta _{p},\phi )={\frac {cos((1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}{cos(-(1/2)*\phi +(1/2)*arcsin(3*sin(\phi )))}}}

fbar:=1/2∗ ∗ -->(fp+fm){\displaystyle fbar:=1/2*(f_{p}+f_{m})}

D2F=d2F(θ θ -->,ϕ ϕ -->)dθ θ -->2{\displaystyle D2F={\frac {d^{2}F(\theta ,\phi )}{d\theta ^{2}}}}

D2Fp=D2F(θ θ -->p,ϕ ϕ -->){\displaystyle D2F_{p}=D2F(\theta _{p},\phi )}

D2Fm=D2F(θ θ -->m,ϕ ϕ -->){\displaystyle D2F_{m}=D2F(\theta _{m},\phi )}

Δ Δ -->:=(3/4∗ ∗ -->(fm− − -->fp))(2/3){\displaystyle \Delta :=(3/4*(f_{m}-f_{p}))^{(}2/3)}

u=Δ Δ -->1/22∗ ∗ -->(1D2Fp+1− − -->D2Fm){\displaystyle u={\sqrt {\frac {\Delta ^{1/2}}{2}}}*({\frac {1}{\sqrt {D2F_{p}}}}+{\frac {1}{\sqrt {-D2F_{m}}}})}

v=2Δ Δ -->1/2∗ ∗ -->(1D2Fp− − -->1− − -->D2Fm){\displaystyle v={\sqrt {\frac {2}{\Delta ^{1/2}}}}*({\frac {1}{\sqrt {D2F_{p}}}}-{\frac {1}{\sqrt {-D2F_{m}}}})}

K(ϕ ϕ -->,ρ ρ -->)≈ ≈ -->2∗ ∗ -->π π -->∗ ∗ -->(u∗ ∗ -->cos(ρ ρ -->∗ ∗ -->fbar)∗ ∗ -->AiryAi(− − -->ρ ρ -->(2/3)∗ ∗ -->Δ Δ -->)/ρ ρ -->(1/3)+v∗ ∗ -->sin(ρ ρ -->∗ ∗ -->fbar)∗ ∗ -->AiryAi(1,− − -->ρ ρ -->(2/3)∗ ∗ -->Δ Δ -->)/ρ ρ -->(2/3)){\displaystyle K(\phi ,\rho )\approx 2*\pi *(u*cos(\rho *fbar)*AiryAi(-\rho ^{(}2/3)*\Delta )/\rho ^{(}1/3)+v*sin(\rho *fbar)*AiryAi(1,-\rho ^{(}2/3)*\Delta )/\rho ^{(}2/3))}

开尔文船波的波峰，由下列两个参数方程式描述

x:=X∗ ∗ -->sin(β β -->)∗ ∗ -->(1− − -->(1/2)∗ ∗ -->sin(β β -->)2){\displaystyle x:=X*sin(\beta )*(1-(1/2)*sin(\beta )^{2})}

y:=X∗ ∗ -->sin(β β -->)2∗ ∗ -->cos(β β -->)/(2∗ ∗ -->M){\displaystyle y:=X*sin(\beta )^{2}*cos(\beta )/(2*M)}

参考文献

Frank J. Oliver, NIST Handbook of Mathematical Functions, 2010, Cambridge University Press

Jame Lighthill Waves in Fluids, Cambridge University Press 1979

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。