重子生成（Baryogenesis）

现代物理学中，其中一个难题就是“为何宇宙中的物质比反物质多？”。整体来说，宇宙的重子数密度是非零的——即物质是存在的。因宇宙学已假定我们所见的粒子是用我们现存的物理学创造的，照理整体重子数应该是零，因为创造物质和反物质时理应是等量的。许多提出对称性破缺的假设机制都认为只要在特定条件下，普通物质（对应反物质）是可以被创造的。这个失衡的情况是异常的少，在宇宙大爆炸之后的瞬间每100亿（10）个粒子中只有一个会这样失衡，但当大部分物质与反物质互相碰触并湮灭后，现存宇宙剩下的就只有重子物质和比它更大量的玻色子。

多数大统一理论（GUTs）明确地否定了重子数的对称性，可用来解释这个矛盾，最典型的是引起以超重X玻色子（下称X）或重希格斯玻色子（T）作媒介的反应。发生这些事件的速率主要决定于媒介 X 或 T 粒子的质量，因此假设这些反应是基于现今多数所见的重子数，那最大质量就可以计算出来，用来解释现存物质的话，会发现速率过慢。这些估计预测，即是用上现时最大可用的还原能量，大量的物料将会周期性地发生自发性质子衰变。

有关实验及证据

质子衰变是各式提议的 GUTs 中少数可观察影响的一种，其他主要是磁单极。两者自1980年代初成为实验物理学中的主要研究焦点。

其中一个大统一理论的预言是，构成通常物质的大部分质量的质子能自发衰变成诸如反电子之类更轻的粒子。其原因在于，在大统一能量下，夸克和反电子之间没有本质的不同。正常情况下一个质子中的三个夸克没有足够能量转变成反电子，由于测不准原理意味着质子中夸克的能量不可能严格不变，所以，其中一个夸克能非常偶然地获得足够能量进行这种转变，这样质子就要衰变。夸克要得到足够能量的概率是如此之低，以至于至少要等100万亿亿亿年（10年--100壤）才能有一次。这比宇宙从大爆炸以来的年龄（大约100亿年，10年）要长得多了。因此，人们会认为不可能在实验上检测到质子自发衰变的可能性。但是，我们可以观察包含极大数量质子的大量物质，以增加检测衰变的机会。（譬如，如果观察的物件含有10个质子，按照最简单的 GUT，可以预料在一年内应能看到多于一次的质子衰变。）

质子衰变曾有一段时期是实验物理学中一个非常触目的领域，但目前为止，所有试图观察这个衰变的实验无一成功。

有一个实验是用了8千吨水在美国俄亥俄州的莫尔顿盐矿里进行的（为了避免其他因宇宙射线引起的会和质子衰变相混淆的事件发生）。由于在实验中没有观测到自发的质子衰变，因此可以估算出，可能的质子寿命至少应为1千万亿亿亿年（10年）。这比简单的大统一理论所预言的寿命更长。然而，一些更精致更复杂的大统一理论预言的寿命比这更长，因此需要用更灵敏的手段对甚至更大量的物质进行检验。

近来日本利用超级神冈探测器在水中探测切连科夫辐射的实验中，指出如果质子完全衰变，半衰期必定至少长达 10 年。

人们进行了一系列的实验，可惜没有一个得到质子衰变的确实证据。

理论衰变过程

尽管质子衰变的观察证据缺乏，但有部分大统一理论（GUTs）依然需要这些观察证据支持。根据一些 GUTs，质子的半衰期大约为 10 年，衰变后会产生正电子和中性π介子，而中性π介子会再度衰变产生两个单位的伽马射线（γ）：

额外的衰变模式是可行的，当中包括直接及透过与 GUT 预测的磁单极催化时的相互作用。虽然这个过程仍未从实验中观察到，但透过将来计划的兆吨级超大尺度探测器，将可进入了实验可测阶段，此类探测器包括日本的Hyper-Kamiokande。

早期的各式大统一理论（GUTs）是首个对质子衰变有一致性的理论，当中预言质子半衰期可能至少 10 年。直至1990年代进行的各项实验和计算，表明质子半衰期不能低于 10 年，那时期的书籍大多提到这个数字以说明重子物质的可能衰变时间。

虽然这现象叫“质子衰变”，但此现象亦可能在中子撞击原子核时出现。自由中子（不在原子核内的中子）已知可以在一个叫“β衰变”的过程中衰变成质子（加一粒电子和一粒反中微子），自由中子的半衰期因为弱相互作用关系而只有10分钟。

衰变算子

Dimension-6 质子衰变算子

它们是 qqqlΛ Λ -->2{\displaystyle {\frac {qqql}{\Lambda ^{2}}}}、dcdcucecΛ Λ -->2{\displaystyle {\frac {d^{c}d^{c}u^{c}e^{c}}{\Lambda ^{2}}}}、ec¯ ¯ -->uc¯ ¯ -->qqΛ Λ -->2{\displaystyle {\frac {{\overline {e^{c}}}{\overline {u^{c}}}qq}{\Lambda ^{2}}}} 和 dc¯ ¯ -->uc¯ ¯ -->qlΛ Λ -->2{\displaystyle {\frac {{\overline {d^{c}}}{\overline {u^{c}}}ql}{\Lambda ^{2}}}}，当中 Λ 是 标准模型的截止尺度（cutoff scale）。所有这些算子都违犯了重子数（baryon number）和轻子数（lepton number），但 B−L 的结合除外。

在 GUT 模型中，一个质量为 ΛGUT 的X或Y玻色子转换可导致最后两个算子以 1Λ Λ -->GUT2{\displaystyle {\frac {1}{\Lambda _{GUT}^{2}}}} 抑制。而质量为 M 的三线峰希格斯玻色子转换可导致全部四个算子以 1/M 抑制。详见二线峰-三线峰分裂问题（Doublet-triplet splitting problem）

Dimension-5 质子衰变算子

在超对称扩展中（例如超对称最小扩展模型，MSSM），包含两个费米子和两个标量费米子的 Dimension-5 算子可从一个质量为 M 的 tripletino 的转换而产生，而标量费米子会转换伴胶子或伴引力子或伴希格斯玻色子并剩下两个费米子，最后一幅总费曼图会出现一个回路（和其他与强相互作用物理有关的复杂因子）。衰变速率会被 1MMSUSY{\displaystyle {\frac {1}{MM_{SUSY}}}} 抑制，当中 MSUSY 是超对称粒子的质量尺度。

Dimension-4 质子衰变算子

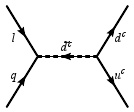
在缺乏 matter parity 的情况下,标准模型的超对称扩展可令最后一个算子以 sdown夸克质量的平方反比抑制，这是与 dimension-4 衰变算子有关：

质子衰变速率只会被 1MSUSY2{\displaystyle {\frac {1}{M_{SUSY}^{2}}}} 抑制，除非那对结合体非常的小，否则衰变速率是非常快的。

参见

B−L

大统一理论（GUT）

X 和Y 玻色子

延伸阅读

K. Hagiwara et al.,"Particle Data Group current best estimates of proton lifetime", Phys. Rev. D 66, 010001 (2002) ISBN 978-0684865768

Adams, Fred and Laughlin, Greg The Five Ages of the Universe : Inside the Physics of Eternity ISBN 0-684-86576-9

Krauss, Lawrence M. Atom : An Odyssey from the Big Bang to Life on Earth ISBN 0-316-49946-3

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。