适用性

从一系列运输方法中选择优化运输成本的一个或多个表现规模经济的连通性和容量约束不同的非凸问题。例如从管道、铁路油槽车、罐车、河驳船或沿海油船中选择或组合的石油产品运输。由于经济批量大小，除了平滑变化之外，成本函数可以有不连续性。

现代工程实践涉及到大量的数值优化。除了在很少一部分重要情形（如无源电路）中，工程问题是非线性的，它们通常是非常复杂。

在实验科学中，一些简单的数据分析（如已知位置和形状但未知幅度的峰的总和的光谱的拟合）可以用线性方法来完成，但一般来说这些问题也是非线性的。通常研究的是含有变量参数的系统的理论模型以及含有未知参数的试验模型。可以试着用数值寻找最优值。这种情况下，除了最优值本身通常还需要对结果的精度进行量度。

定义

令 n、m、p为正整数。令 X 为 R 的一个子集，令 f、gi 和 hj 为 X 的实值函数（英语：real-valued function），对每个 i 属于 {1, …, m} 及每个 j 属于 {1, …, p}。

非线性最小化问题是下面形式的最优化问题

非线性最大化问题定义方式类似。

约束集的可能类型

约束集的性质有若干可能性，也被称为可行集或可行域（英语：feasible region）。

无解问题（infeasible problem）是指没有一组变数可以满足所有的约束，也就是约束之间有互相矛盾的情形，没有解存在。

有解问题（feasible problem）是指至少有一组变数可以满足所有的约束条件。

无界限问题（unbounded problem）是一个有解问题，其变数没有上限限制，因此没有最佳解，因为总会有一组变数使得目标函数比其他组的变数有更好的结果。

求解问题的方法

若目标函数f为线性，约束的空间为多胞形，此问题是线性规划问题，可以用许多著名的线性规划解来求解。

若目标函数为凹函数（最大化问题）或是凸函数（最小化问题），且约束为凸集，此问题称为凸规划问题，大部分情形下可以用凸优化的方式来求解。

若目标函数是凹函数和凸函数的比值（最大化问题）及约束为凸集，此问题可以用分数规划（英语：fractional programming）的方式转换为凸集的最优化问题。

许多方式可以解非凸集的问题。其一个方式是用线性规划问题的特殊公式，另一种方式则是用分支定界法（英语：branch and bound），将问题分为几个可以用凸集法（最小化问题）求解或是线性近似的子集合，较小区域内的总成本会有一下限。在随后的分区后，在一些点上其成成本会等于所有近似解的下限，此解即为实际解。此解虽然不一定唯一，不过是为最佳解。若已确认可能的最佳解和已找到的解之间的误差在容许值内，可以提早结丛此算法。这些点称为ε-最佳。若要在有限内结丛，一般就需要在ε-最佳点结丛。尤其在大型的、困难的问题，或是问题有不确定的成本或价值，但不确定以由适当的信赖性估测所估测时，更需要在ε-最佳点结丛的技巧。

在可微函数及约束规范的条件下，卡罗需－库恩－塔克条件（KKT条件）是有最佳解的必要条件。在凸集的条件下，这也是充份条件。若其中有些函数是不可微分的，也可以用次导数条件的卡罗需－库恩－塔克条件。

例子

2维实例

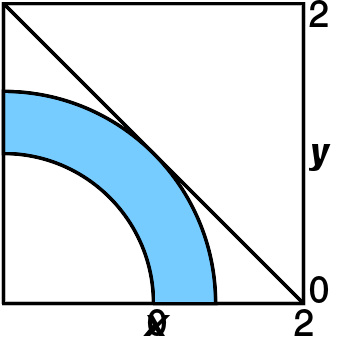
线的交点及约束空间表示了该解。可达到的最优值轮廓线（目标值为给定值的轨迹）。

可以用下列约束来定义一个简单问题

需要最大化的目标函数为

其中 x = (x1, x2)。解决二维问题.

3维实例

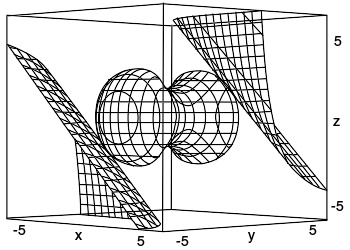
位于中部的上面曲面与约束空间相交的部分表示解

用下面这些约束就可以定义另一个简单的问题

需要最大化的目标函数为

其中 x = (x1, x2，x3).解决三维问题。

应用

工程中用到非线性优化，例如建立储油池的计算模型， 或油气藏工程的决策制定。

参见

曲线拟合

最小二乘法

线性规划

nl (文件格式)（英语：nl (format)）

最优化

最优化软件列表（英语：List of optimization software）

维尔纳·费恩雪尔（英语：Werner Fenchel）

延伸阅读

Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.

Bazaraa, Mokhtar S. and Shetty, C. M. (1979). Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.

Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.

Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A.Numerical optimization: Theoretical and practical aspects. Universitext Second revised ed. of translation of 1997 French. Berlin: Springer-Verlag. 2006: xiv+490. ISBN 3-540-35445-X. MR 2265882. doi:10.1007/978-3-540-35447-5. 

Luenberger, David G.; Ye, Yinyu. Linear and nonlinear programming. International Series in Operations Research & Management Science 116 Third. New York: Springer. 2008: xiv+546. ISBN 978-0-387-74502-2. MR 2423726. 

Nocedal, Jorge and Wright, Stephen J. (1999). Numerical Optimization. Springer. ISBN 0-387-98793-2.

Jan Brinkhuis and Vladimir Tikhomirov, "Optimization: Insights and Applications", 2005, Princeton University Press

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。