描述

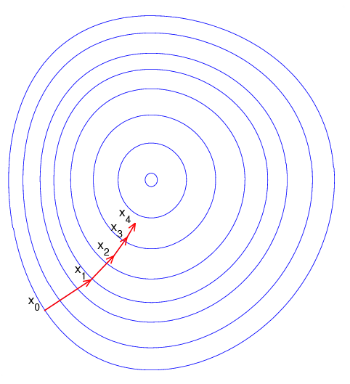
梯度下降法的描述。

梯度下降方法基于以下的观察：如果实值函数F(x){\displaystyle F(\mathbf {x} )}在点a{\displaystyle \mathbf {a} }处可微且有定义，那么函数F(x){\displaystyle F(\mathbf {x} )}在a{\displaystyle \mathbf {a} }点沿着梯度相反的方向 − − -->∇ ∇ -->F(a){\displaystyle -\nabla F(\mathbf {a} )} 下降最快。

因而，如果

对于γ γ -->>0{\displaystyle \gamma >0}为一个够小数值时成立，那么F(a)≥ ≥ -->F(b){\displaystyle F(\mathbf {a} )\geq F(\mathbf {b} )}。

考虑到这一点，我们可以从函数F{\displaystyle F}的局部极小值的初始估计x0{\displaystyle \mathbf {x} _{0}}出发，并考虑如下序列 x0,x1,x2,… … -->{\displaystyle \mathbf {x} _{0},\mathbf {x} _{1},\mathbf {x} _{2},\dots }使得

因此可得到

如果顺利的话序列(xn){\displaystyle (\mathbf {x} _{n})}收敛到期望的极值。注意每次迭代步长γ γ -->{\displaystyle \gamma }可以改变。

右侧的图片示例了这一过程，这里假设F{\displaystyle F}定义在平面上，并且函数图像是一个碗形。蓝色的曲线是等高线（水平集），即函数F{\displaystyle F}为常数的集合构成的曲线。红色的箭头指向该点梯度的反方向。（一点处的梯度方向与通过该点的等高线垂直）。沿着梯度下降方向，将最终到达碗底，即函数F{\displaystyle F}值最小的点。

例子

梯度下降法处理一些复杂的非线性函数会出现问题，例如Rosenbrock函数

其最小值在(x,y)=(1,1){\displaystyle (x,y)=(1,1)}处，数值为f(x,y)=0{\displaystyle f(x,y)=0}。但是此函数具有狭窄弯曲的山谷，最小值(x,y)=(1,1){\displaystyle (x,y)=(1,1)}就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。

下面这个例子也鲜明的示例了"之字"的上升（非下降），这个例子用梯度上升（非梯度下降）法求F(x,y)=sin⁡ ⁡ -->(12x2− − -->14y2+3)cos⁡ ⁡ -->(2x+1− − -->ey){\displaystyle F(x,y)=\sin \left({\frac {1}{2}}x^{2}-{\frac {1}{4}}y^{2}+3\right)\cos(2x+1-e^{y})}的极大值（非极小值，实际是局部极大值）。

缺点

梯度下降法的缺点包括：

靠近极小值时速度减慢。

直线搜索可能会产生一些问题。

可能会“之字型”地下降。

上述例子也已体现出了这些缺点。

参阅

参考文献

Mordecai Avriel (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.

Jan A. Snyman (2005). Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer Publishing. ISBN 0-387-24348-8

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。