自然语言中的量化

所有已知人类语言都使用量化，即使是那些没有完整的数字系统的语言（Wiese 2004）。例如：

“我最近订的所有玻璃都碎了”。

“站在河边的一些人带着白臂章”。

“我交谈的多数人都没有从属的俱乐部”。

“在候诊室里的所有人都对Ballyhoo医生有至少一个抱怨”。

“在他的班级中有些人能够正确的回答我提出的所有问题”。

“大量的人是聪明的”。

不存在简单的方式把这些表达重新公式化为句子们的合取或析取，它们每个都有个体的简单谓词如“酒杯碎了”。这些例子也暗示了在自然语言中的量化表达式构造可以是语法上非常复杂的。幸运的是，对于数学断言，量化过程在语法上是更加直接的。

研究自然语言中的量化比研究形式语言的量化要难很多。这部分的由于自然语言句子的文法结构可能隐藏了逻辑结构的事实。而数学约定严格的为形式语言量词指定了有效范围；为自然语言指定有效性的范围要求处理不平凡的语义问题。

Montague文法给出了新颖的自然语言的形式语义。它提起争论说它比弗雷格、罗素和蒯因的传统处理更加自然的对自然语言的形式化表现。

数学论断中的量词

我们开始讨论在非正式数学讨论中的量化。考虑下列陈述

量词的嵌套

考虑下列语句：

下面这个断言中的量词的意义就非常不同了：

这展示了量词嵌套的时候的基本要点：量词间隔的次序是绝对重要的。不平常些的例子是来自数学分析的一致连续的概念，只是通过对换了两个量词的位置，它就不同于更加熟悉的逐点连续的概念。

量词的范围

每个量词都涉及一个特定的变量和这个变量的论域或“量化范围”。量化的范围指定这个变量采用的值的集合。在上面的例子中，量化的范围是自然数的集合。量化范围的指定允许我们表达出，在断言一个谓词对某些自然数成立和对某些实数成立之间的区别。说明性的约定经常保留某些变量名字，比如n保留给自然数，x保留给实数，尽管依赖于命名约定一般不能工作，因为变量的范围在数学论证过程中是可以变更的。

限制论域的更自然的方式是使用“监控量化”。例如：

早某些数学理论中你可以预先假定一个固定的单一论域。例如，在Zermelo Fraenkel集合论中，变量范围是在所有集合之上。在这种情况下，可以监控量词来模拟更小的量化范围。如上述例子中

在Zermelo-Fraenkel集合论中，你可以说

量词的记号

全称量词的传统符号是∀，它倒过来的字母A，表示单词“all”。存在量词的相应的符号是∃，它是反过来的字母E，表示单词“exists”。相应的量化表达式构造如下：

这里的P指示一个公式。有很多变体被使用了，比如

所有这些变体都同样适用于全称量化和存在量化。

二十世纪早期的文献不使用∀符号。典型的记号是用（x）P来表达"对于所有的x，P"和"（∃x）P"表示"存在x使得P"。∃符号是皮亚诺在1890年左右提出的。后在，在1930年左右，Gerhard Gentzen介入了∀符号来表示全称量化。弗雷格的《概念文字》使用完全不同记号，它根本就不包括存在量词；∃x:P总是用概念文字表达为等价的¬∀x:¬P。

注意某些版本的记号明确的提及了量词的范围。量词的范围总是必须指定，但是对于给定的数学理论，可以用多种方式来做：

为每个量词假定一个固定的论域，比如Zermelo Fraenkel集合论，

预先固定多个论域并要求每个变量有一个声明了域，它就是这个变量的类型。这类似于强类型的计算机编程语言，那里的变量有声明过的类型。

明确的提及量化的范围，可能使用在这个域中所有对象的集合或在这个域中对象的类型符号。

还要注意在特定限制下，也就是在不发生变量捕获条件下，你可以使用任何变量替代任何其他变量作为量化变量。即使这种记号使用了有类型的变量，你仍可以使用这种类型的任何变量。变量捕获的问题是极其重要的，并在下面的形式语义章节中讨论。

非正式的，"∀x"或"∃x"也可以出现在P（x）之后，甚至在P（x）的中间，如果它是个长短语的话。正式的说，介入虚（dummy）变量的短语在标准上要位于前面。

注意数学公式混合了量词的符号表达和自然语言量词，比如：

唯一量化的关键字包括：

你使用代名词来避免变量名字如x。例如：

形式语义

数理语义是用形式化的数学上的特定语言表达的研究意义的数学应用。它有三个要素：通过语法的一类对象的数学规定，各种语义域的数学规定，和在二者之间的关系，它通常表达为从语法对象到语义对象的函数。在本文中，我们只致力于描述量词元素如何解释的问题。

在本文中，我们只考虑带有函数符号的一阶逻辑。我们建议读者看模型论的文章获得关于在这个逻辑框架内公式释义的更详细信息。公式的语法可以用语法树给出。量词有范围，而变量x是自由的，如果它不在这个变量的量化范围内。所以在

中，x和y二者在C（y,x）中的出现是自由的。

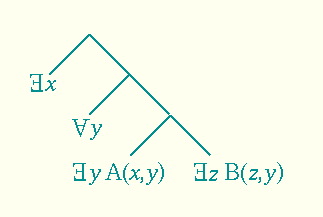
展示范围和变量捕获的语法树

一阶谓词演算的释义假定给出一个个体域X。自由变量是x1, ..., xn的一个公式A被解释为n个参数的一个布尔值函数F（v1, ..., vn），这里的每个参数都定范围在域X上。布尔值意味着这个函数采用值T（解释为真）或F（解释为假）中的一个。公式

的释义是n-1个参数的函数G，使得G（v1, ...,vn-1） = T，当且仅当对于在X中所的w有F（v1, ..., vn-1, w） = T。如果对于至少w的一个值，有F（v1, ..., vn-1, w） = F，则G（v1, ..,vn-1） = F。类似的，公式

的释义为n-1个参数的函数H，使得H（v1, ...,vn-1） = T，当且仅当对于至少一个w有F（v1, ...,vn-1, w） = T，否则H（v1, ..., vn-1） = F。

唯一量化的语义要求带有等号的一阶谓词演算。这意味着这里要有一个显著的二元谓词"="；语义也要相应的修改来使"="总是被解释为在X上的二元等价关系。

被解释为n-1个参数的函数，它是如下两个释义的逻辑与

几个、多个和其他程度的量词

我们只考虑了在数学中的全称、存在和唯一量化。它们都不能用来量化如下

今晚在舞场有很多舞女。

尽管在本文中我们没有考虑自然语言的语义，我们将尝试用如下类型的自然语言为断言提供语义

有很多n < 100的整数，使得n能被2或3或5整除。

一种可能的解释机制可以获得如下：假设除了语义域X之外，我们还给出在X上定义一个概率测度P和截断数0 < a ≤ b ≤ 1。如果A是带有自由变量x1,...,xn的公式，它的释义是变量v1,...,vnthe的函数F，则

的释义是v1,...,vn-1的函数，它是T当且仅当

，否则是F。类似的，

的释义是v1,...,vn-1的函数，它是F当且仅当

，否则是T。我们已经完全避免了关于释义函数的测度性的技术问题的讨论；其中某些技术问题要求Fubini定理。

我们还要警告读者这种语义相应的逻辑是非常复杂的。

形式化的历史

在形式逻辑中的量化的第一个基于变量的处理直到19世纪才出现，尽管词项逻辑以同在自然语言很紧密的方式处理量化，但不适合于形式分析。亚里士多德逻辑在公元前1世纪给出了“所有”、“某些”和“没有”量词和对真势模态的处理。

第一个基于变量的逻辑处理是弗雷格的《概念文字》，紧随在查尔斯·皮尔士独立的公式化了存在图之后。弗雷格的方法被证明更有影响，因为它被皮亚诺接受，尽管Pierce的逻辑最近更加引起逻辑学家对异类推理和图表推理的兴趣。

量化的第一个严格的表示法出现在弗雷格的《概念文字》。弗雷格使用在变量名下划的曲线来指示在它随后的公式中这个变量是被全称量化的。弗雷格没有给存在量化特殊的记号，而是使用等价的∼ ∼ -->∀ ∀ -->x:∼ ∼ -->… … -->{\displaystyle \sim \forall x:\sim \ldots }。

在怀特海和罗素的《数学原理》中，弗雷格的记号被简化了。使用公式“(x)ϕ ϕ -->{\displaystyle (x)\phi }”来指示这个公式φ对于x的所有的值都是真的。存在量化被写为“(∃ ∃ -->x)ϕ ϕ -->{\displaystyle (\exists x)\phi }”；∃符号自身是皮亚诺在1897年首次使用的。

∀符号是后来发明的，它是格哈德·根岑在1935年模仿皮亚诺的∃符号而发明。

引用

Jon Barwise and John Etchemendy, 2000. Language Proof and Logic. CSLI (University of Chicago Press) and New York: Seven Bridges Press. A gentle introduction to first-order logic by two first-rate logicians.

Crosby, Alfred W.（1996）The Measure of Reality: Quantification and Western Society, 1250-1600. Cambridge University Press.

Gottlob Frege, 1879. Begriffsschrift. Translated in Jean van Heijenoort, 1967. From Frege to Godel: A Source Book on Mathematical Logic, 1879-1931. Harvard Univ. Press. The first appearance of quantification.

David Hilbert and Wilhelm Ackermann, 1950 (1928). Principles of Theoretical Logic. Chelsea. Translation of Grundzüge der theoretischen Logik. Springer-Verlag. The 1928 first edition is the first time quantification was consciously employed in the now-standar manner, namely as binding variables ranging over some fixed domain of discourse. This is the defining aspect of first-order logic.

Charles Peirce, 1885, "On the Algebra of Logic: A Contribution to the Philosophy of Notation, American Journal of Mathematics 7: 180-202. Reprinted in Kloesel, N. et al, eds., 1993. Writings of C. S. Peirce, Vol. 5. Indiana Univ. Press. The first appearance of quantification in anything like its present form.

Hans Reichenbach, 1975 (1947). Elements of Symbolic Logic, Dover Publications. The quantifiers are discussed in chapters §18 "Binding of variables" through §30 "Derivations from Synthetic Premises".

Wiese, 2003. Numbers, language, and the human mind. Cambridge University Press. ISBN 0-521-83182-2.

Westerstahl, Dag, 2001, "Quantifiers," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic. Blackwell.

参见

自由变量和约束变量

句子 (数理逻辑)

免责声明：以上内容版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。