



菱形十二面体
菱形十二面体,截角菱形十二面体截角菱形十二面体截角菱形十二面体的展开图将菱形十二面体的六个发出四条棱的顶点截去,就可以得到一个截角菱形十二面体。参见卡塔兰立体对偶多面体
截角菱形十二面体
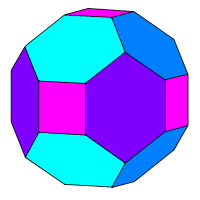
截角菱形十二面体
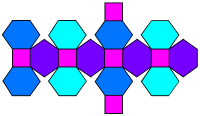
截角菱形十二面体的展开图
将菱形十二面体的六个发出四条棱的顶点截去,就可以得到一个截角菱形十二面体。
参见
卡塔兰立体
对偶多面体
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
——— 没有了 ———
编辑:阿族小谱

文章价值打分
- 有价值
- 一般般
- 没价值
当前文章打 0 分,共有 0 人打分
文章观点支持

0

0
文章很值,打赏犒劳一下作者~

发表评论
写好了,提交
{{item.label}}
{{commentTotal}}条评论
{{item.userName}}
发布时间:{{item.time}}
{{item.content}}
回复
举报


打赏作者
“感谢您的打赏,我会更努力的创作”
— 请选择您要打赏的金额 —
{{item.label}}


{{item.label}}

打赏成功!
“感谢您的打赏,我会更努力的创作”
返回
打赏
私信
24小时热门
推荐阅读
· 菱形三十面体
参见卡塔兰立体对偶多面体
· 正十二面体
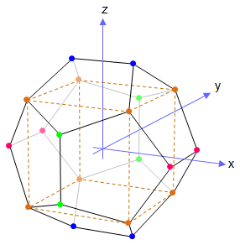
性质面的图形:正五边形面的数目:12边的数目:30顶点数目:20二面角角度:θθ-->=arccos-->(−−-->15)=2arctan-->φφ-->≈≈-->116.5650512∘∘-->{\displaystyle{\boldsymbol{\theta}}=\arccos\left(-{\frac{1}{\sqrt{5}}}\right)=2\arctan\varphi\approx116.5650512^{\circ}}如果正十二面体棱长为a:表面积:A=325+105a2≈≈-->20.645728807a2{\displaystyleA=3{\sqrt{25+10{\sqrt{5}}}}a^{2}\approx20.645728807a^{2}}体积:V=14(15+75)a3≈≈-->7.6631189606a3{\displaystyleV={\frac{1}...
· 菱形
由菱形组成的多面体立方体、菱面体(英语:Rhombohedron)、三角偏方面体、菱形十二面体、菱形二十面体、菱形三十面体、菱形九十面体。
· 二面体群
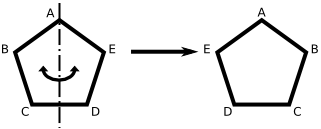
生成元与关系抽象言之,首先考虑n{\displaystylen}阶循环群Cn{\displaystyleC_{n}}。反射ττ-->:x↦↦-->x−−-->1{\displaystyle\tau:x\mapstox^{-1}}是Cn{\displaystyleC_{n}}上的自同构,而且ττ-->2=id{\displaystyle\tau^{2}={\rm{id}}}。定义二面体群为半直积任取Cn{\displaystyleC_{n}}的生成元σσ-->{\displaystyle\sigma},D2n{\displaystyleD_{2n}}由σσ-->,ττ-->{\displaystyle\sigma,\tau}生成,其间的关系是D2n{\displaystyleD_{2n}}的元素均可唯一地表成σσ-->kττ-->h{\d...
· 多面体
经典多面体在经典意义上,一个多面体是一个三维形体,它由有限个多边形面组成,每个面都是某个平面的一部分,面相交于边,每条边是直线段,而边交于点,称为顶点。立方体,棱锥和棱柱都是多面体的例子。多面体包住三维空间的一块有界体积;有时内部的体也视为多面体的一部分。一个多面体是多边形的三维对应。多边形,多面体和更高维的对应物的一般术语是多胞体。参见柏拉图立体阿基米德立体/半正多面体棱柱及反棱柱Johnson多面体三角面体卡塔兰立体星形正多面体双棱锥
关于我们

关注族谱网 微信公众号,每日及时查看相关推荐,订阅互动等。
APP下载

下载族谱APP 微信公众号,每日及时查看

扫一扫添加客服微信















